Chapter 26 Electricity and Magnetism Electric Field Continuous







- Slides: 34

Chapter 26 Electricity and Magnetism Electric Field: Continuous Charge Distribution 1

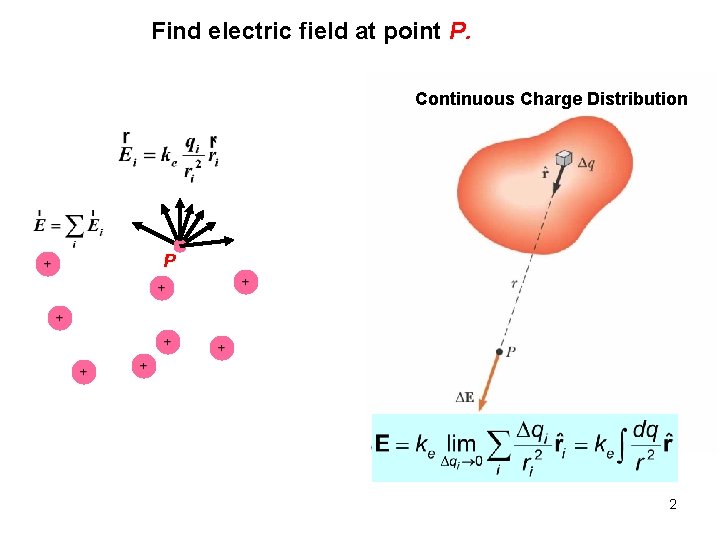
Find electric field at point P. Continuous Charge Distribution P 2

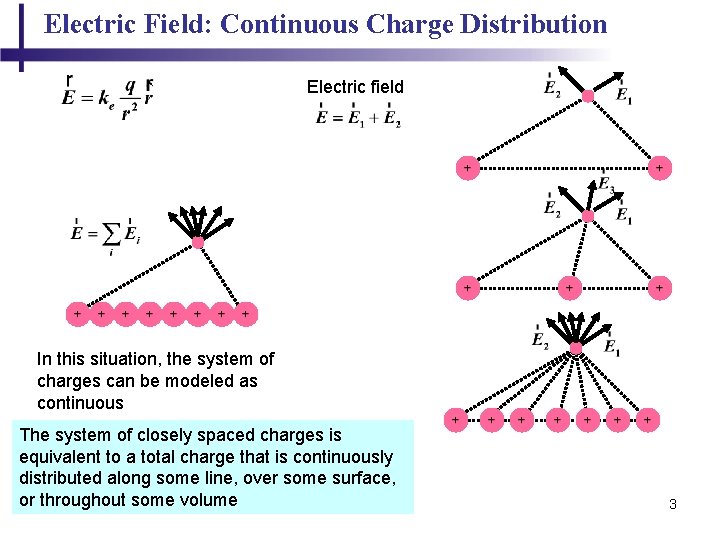
Electric Field: Continuous Charge Distribution Electric field In this situation, the system of charges can be modeled as continuous The system of closely spaced charges is equivalent to a total charge that is continuously distributed along some line, over some surface, or throughout some volume 3

Electric Field: Continuous Charge Distribution The total electric charge is Q. What is the electric field at point P ? P P linear volume Q P Q surface Q 4

Continuous Charge Distribution: Charge Density The total electric charge is Q. Volume V Linear, length L Amount of charge in a small volume dl: Q Linear charge density Q Amount of charge in a small volume d. V: Volume charge density Surface, area A Q Amount of charge in a small volume d. A: Surface charge density 5

Electric Field: Continuous Charge Distribution Procedure: – Divide the charge distribution into small elements, each of which contains Δq – Calculate the electric field due to one of these elements at point P – Evaluate the total field by summing the contributions of all the charge elements Symmetry: take advantage of any symmetry to simplify calculations For the individual charge elements Because the charge distribution is continuous 6

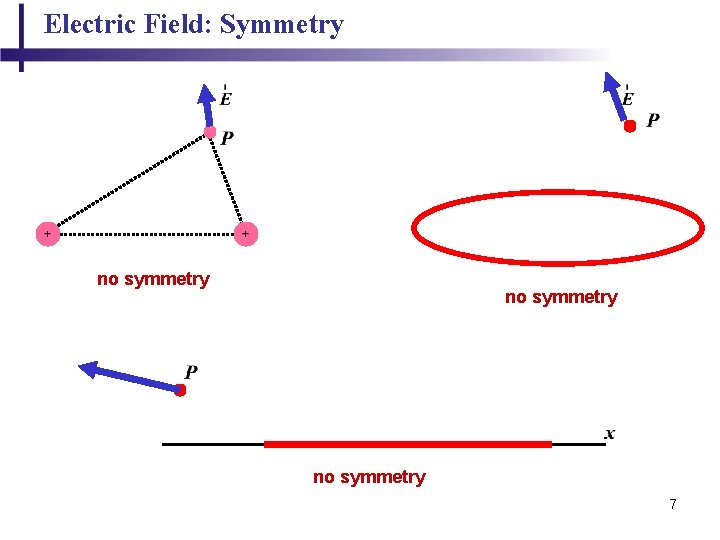
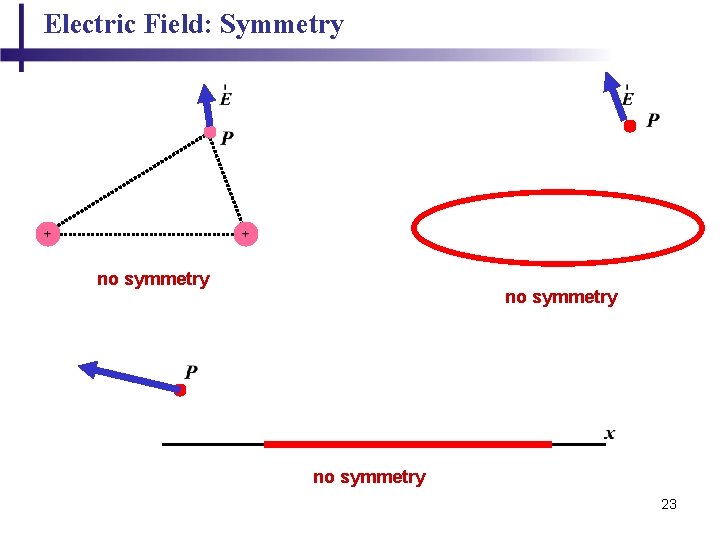
Electric Field: Symmetry no symmetry 7

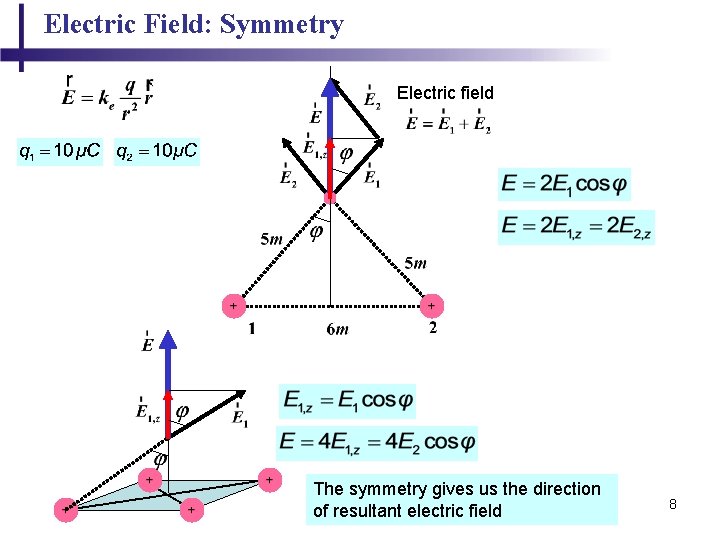
Electric Field: Symmetry Electric field The symmetry gives us the direction of resultant electric field 8

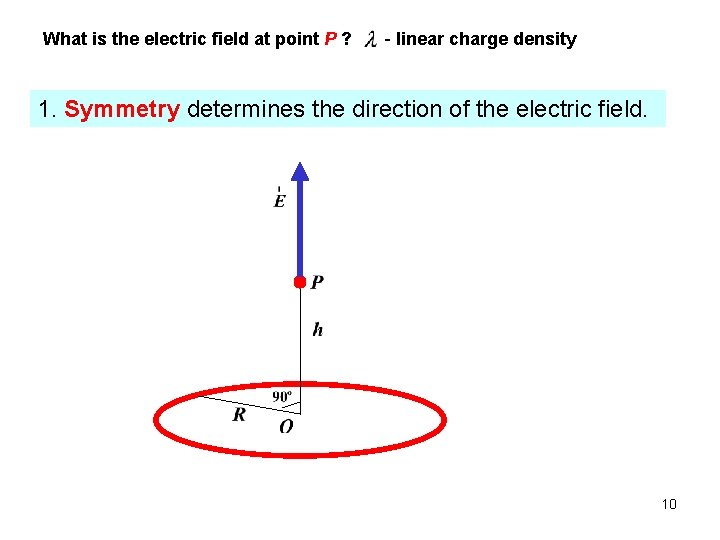
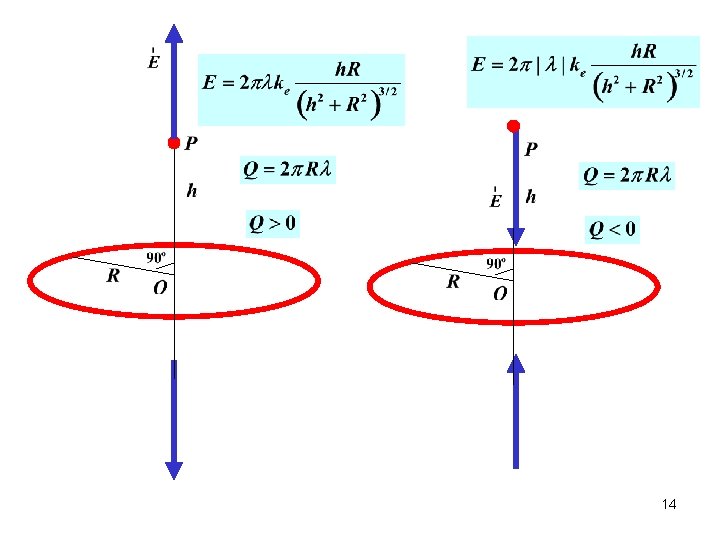
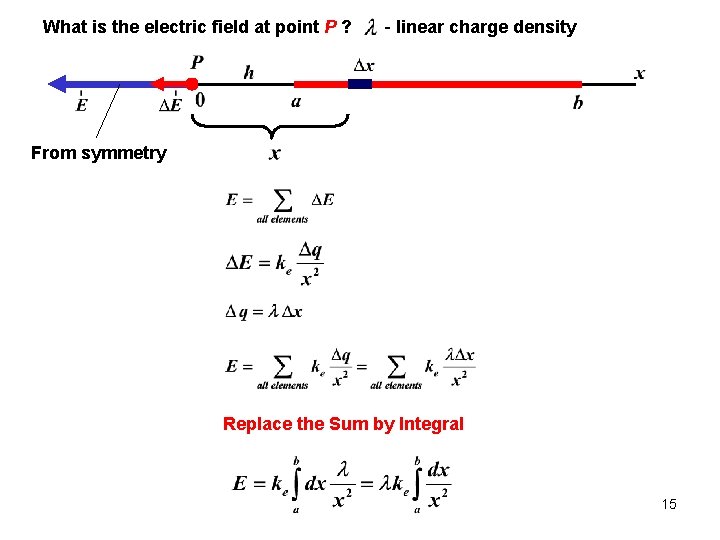
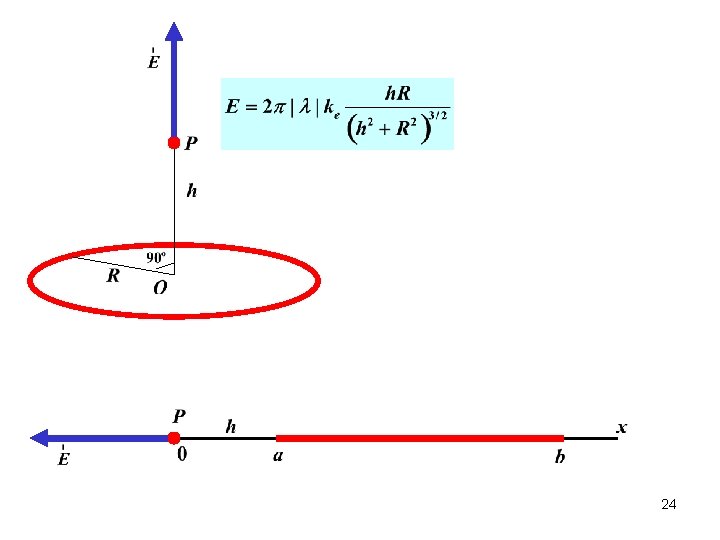
Electric Field: Continuous Charge Distribution What is the electric field at point P ? - linear charge density 9

What is the electric field at point P ? - linear charge density 1. Symmetry determines the direction of the electric field. 10

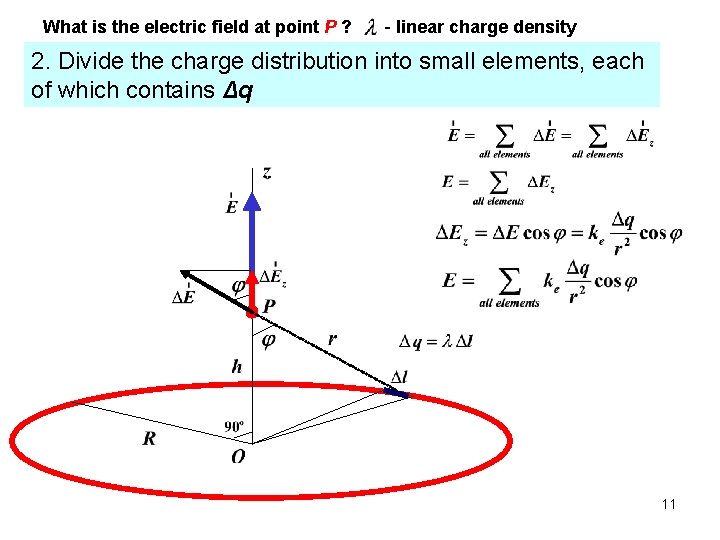
What is the electric field at point P ? - linear charge density 2. Divide the charge distribution into small elements, each of which contains Δq 11

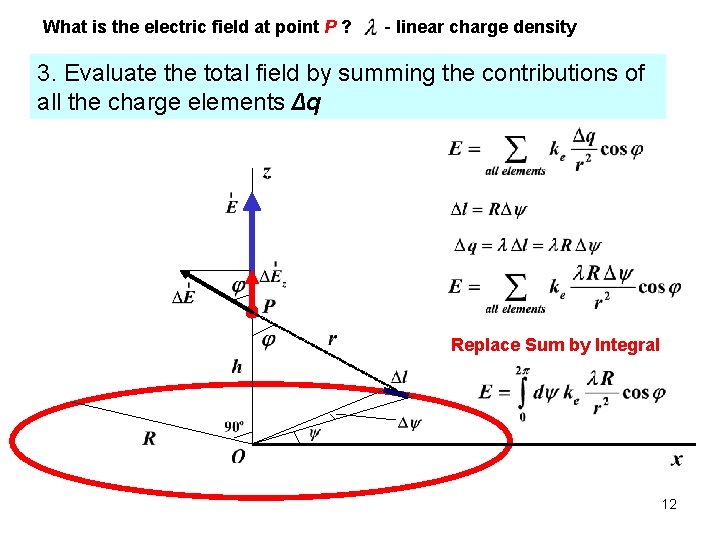
What is the electric field at point P ? - linear charge density 3. Evaluate the total field by summing the contributions of all the charge elements Δq Replace Sum by Integral 12

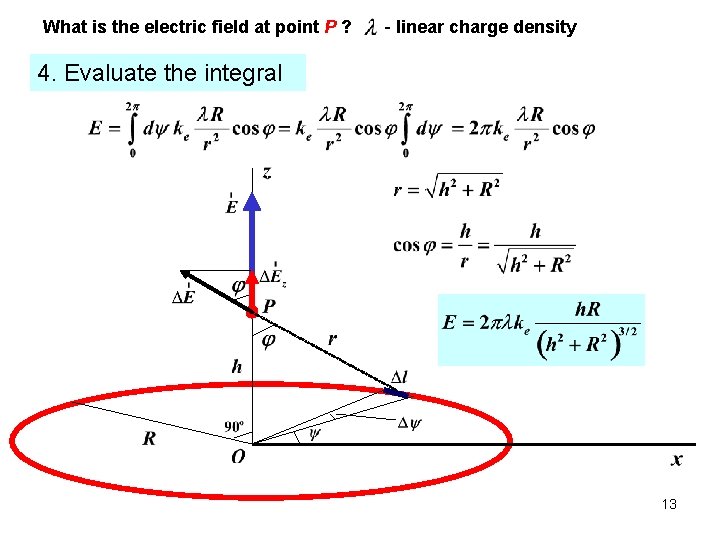
What is the electric field at point P ? - linear charge density 4. Evaluate the integral 13

14

What is the electric field at point P ? - linear charge density From symmetry Replace the Sum by Integral 15

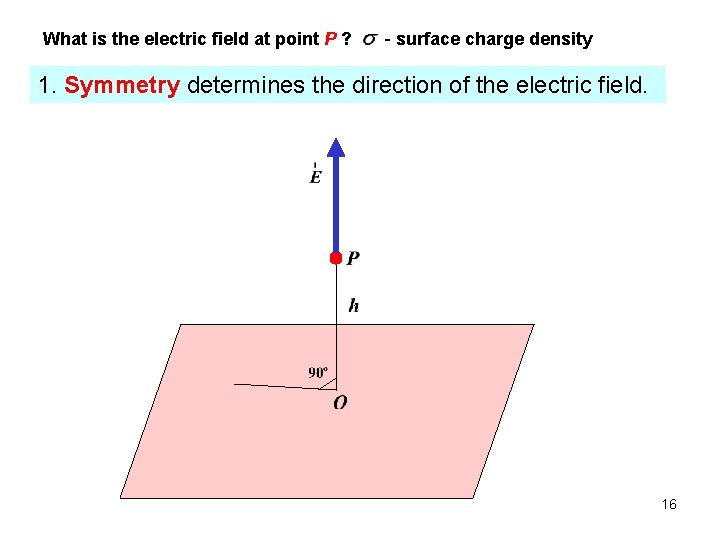
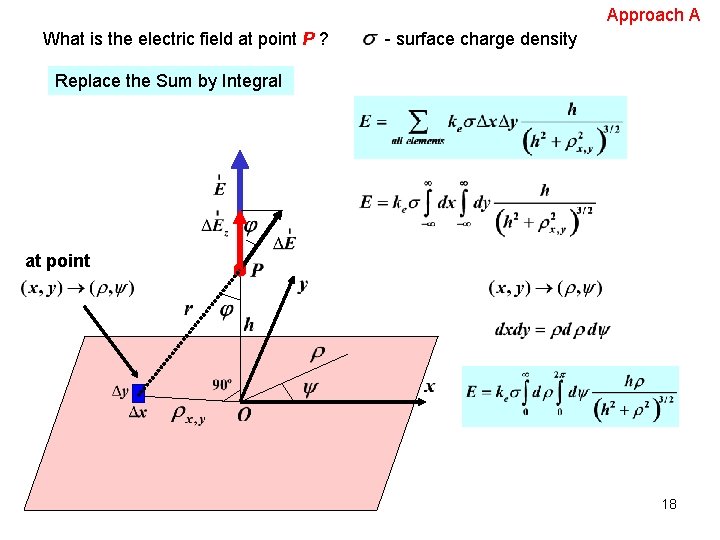
What is the electric field at point P ? - surface charge density 1. Symmetry determines the direction of the electric field. 16

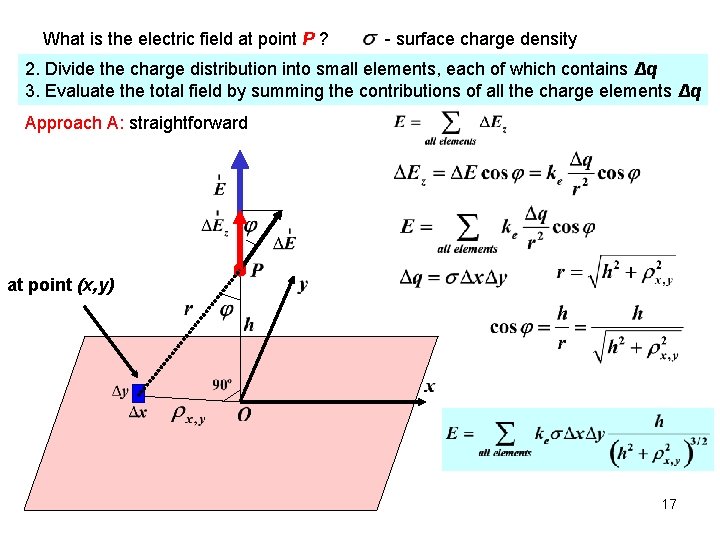
What is the electric field at point P ? - surface charge density 2. Divide the charge distribution into small elements, each of which contains Δq 3. Evaluate the total field by summing the contributions of all the charge elements Δq Approach A: straightforward at point (x, y) 17

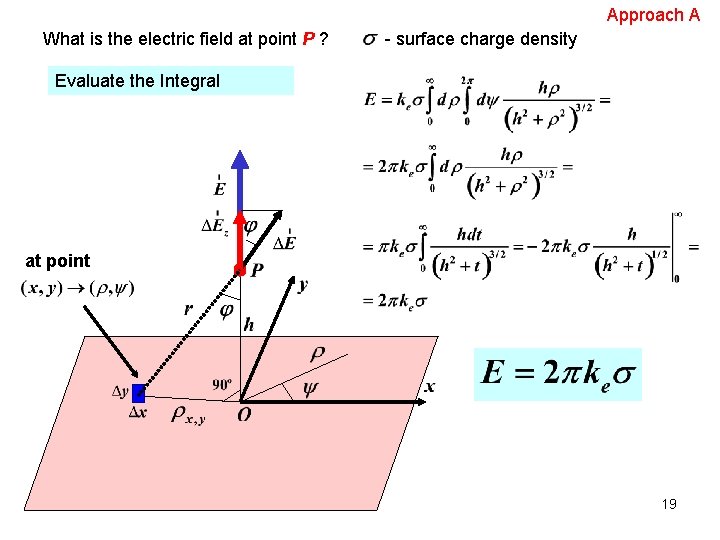
Approach A What is the electric field at point P ? - surface charge density Replace the Sum by Integral at point 18

Approach A What is the electric field at point P ? - surface charge density Evaluate the Integral at point 19

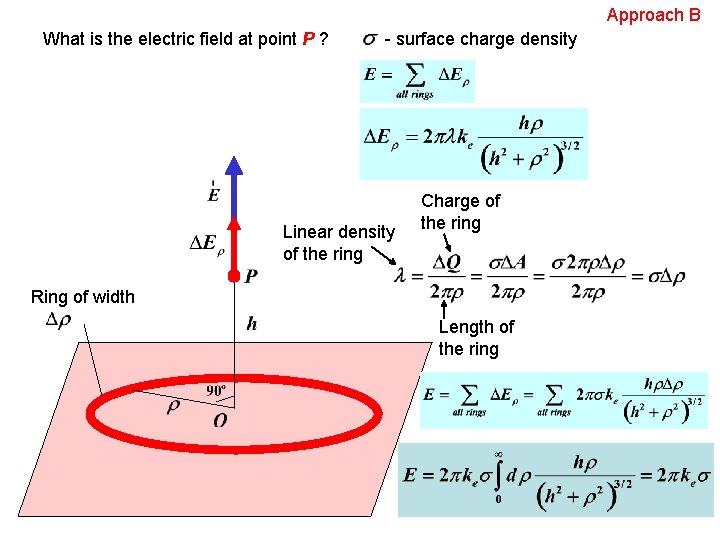
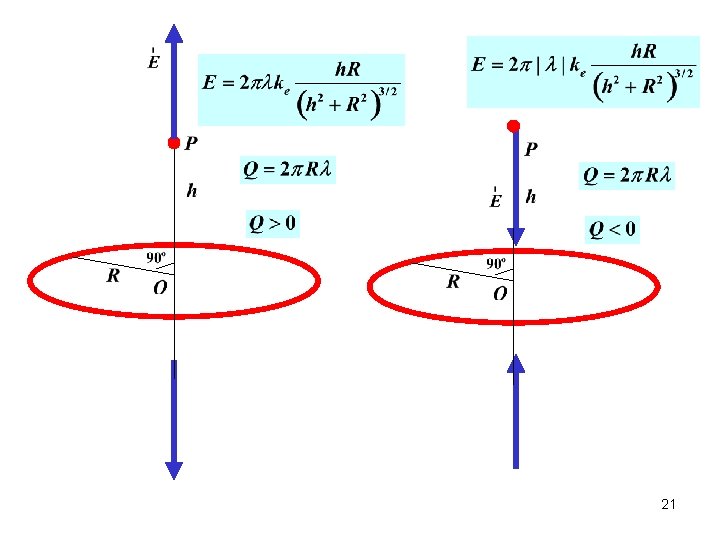
Approach B What is the electric field at point P ? - surface charge density Linear density of the ring Charge of the ring Ring of width Length of the ring 20

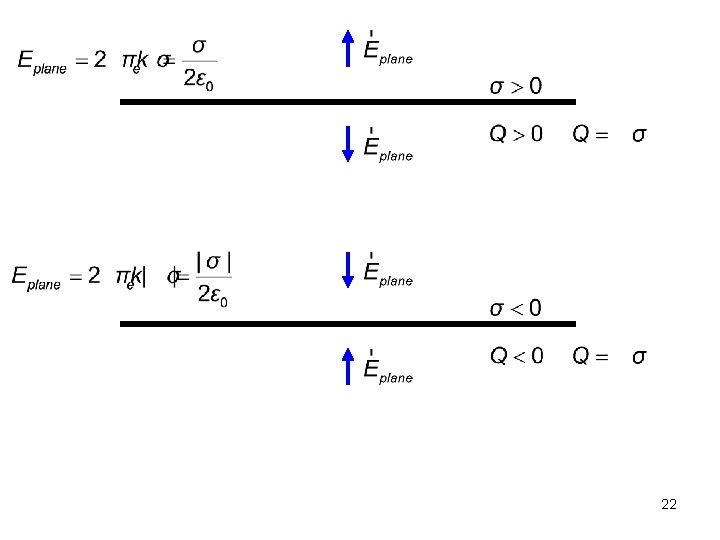
21

22

Electric Field: Symmetry no symmetry 23

24

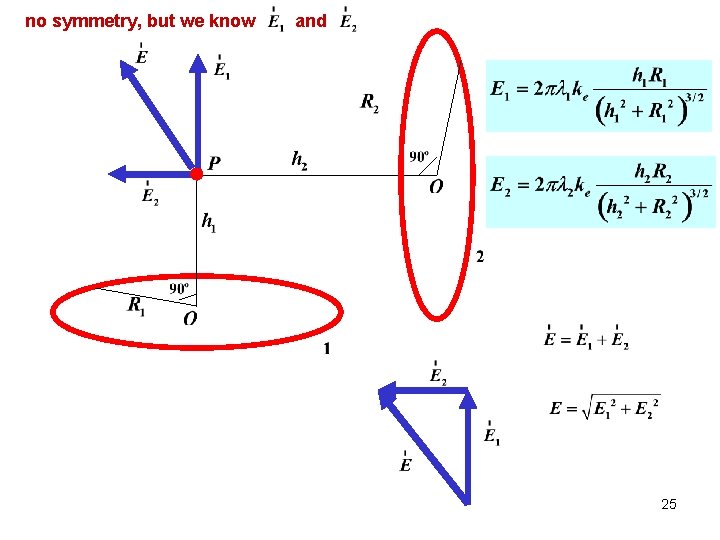
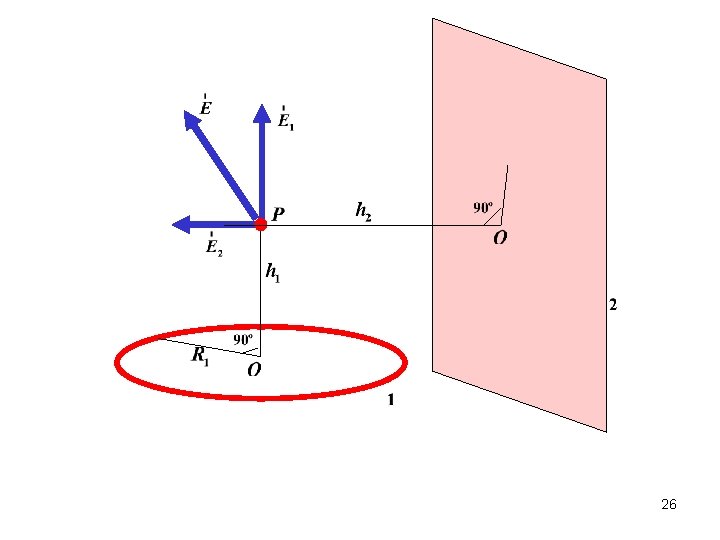
no symmetry, but we know and 25

26

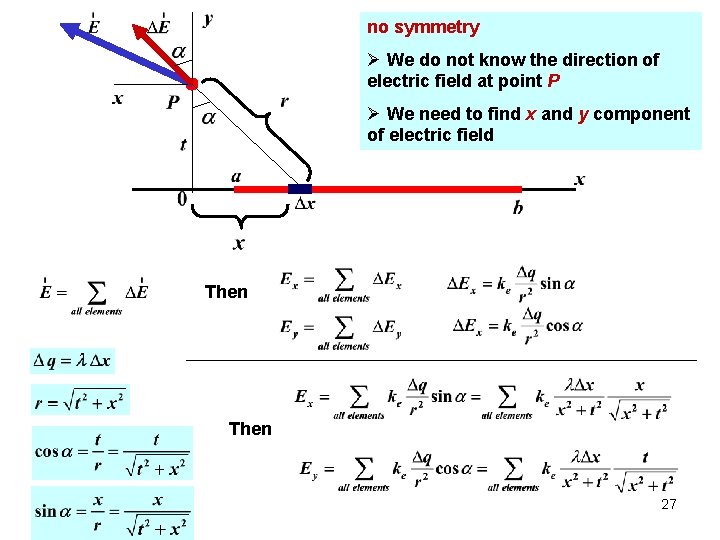
no symmetry Ø We do not know the direction of electric field at point P Ø We need to find x and y component of electric field Then 27

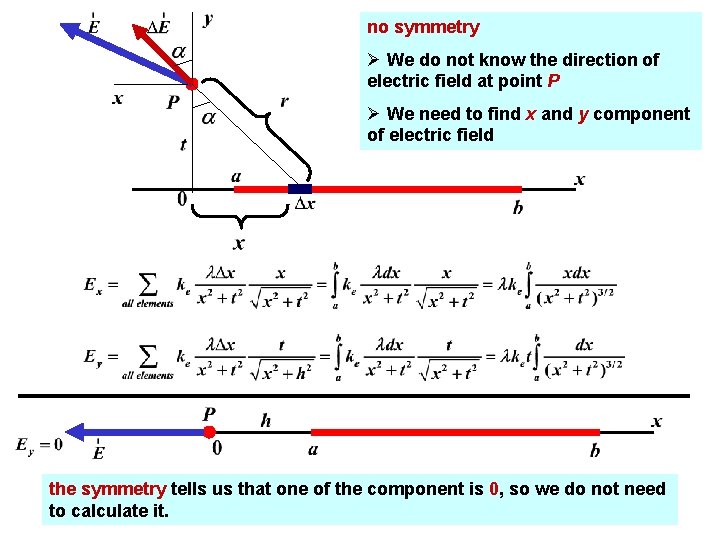
no symmetry Ø We do not know the direction of electric field at point P Ø We need to find x and y component of electric field the symmetry tells us that one of the component is 0, so we do not need 28 to calculate it.

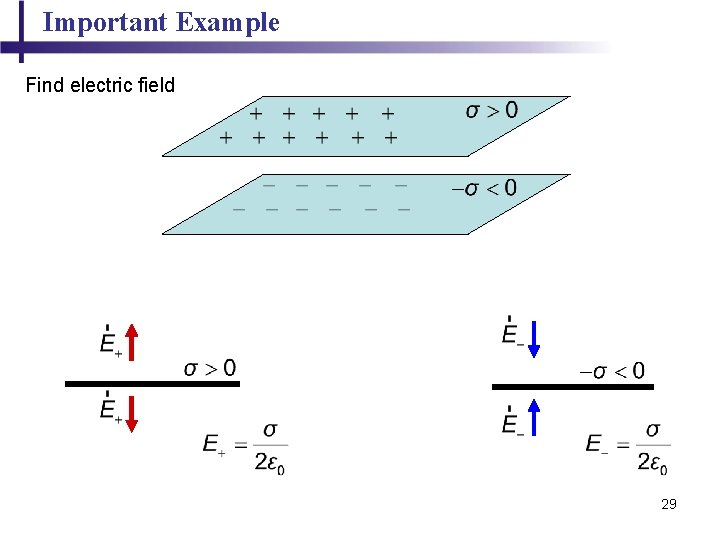
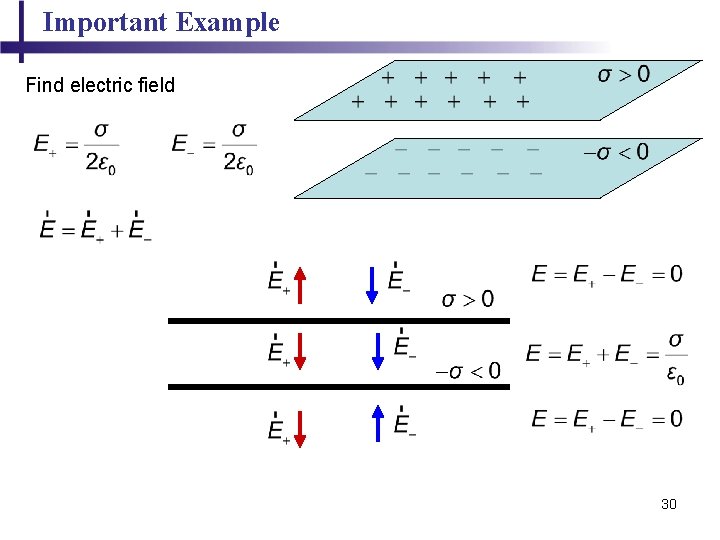
Important Example Find electric field 29

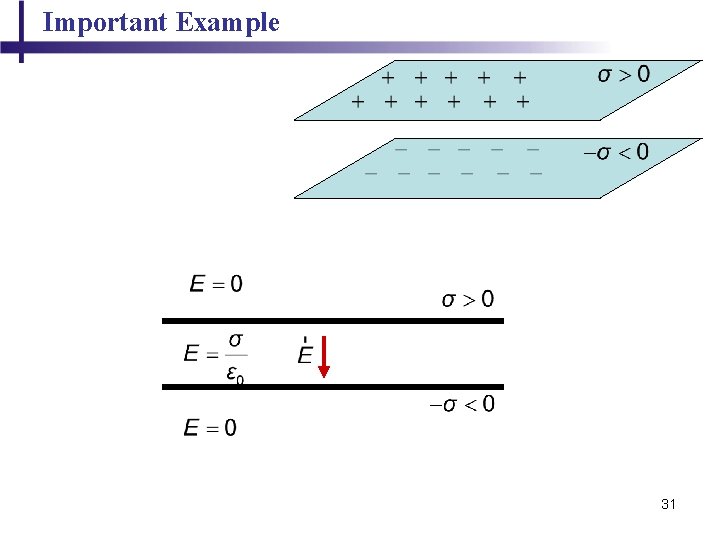
Important Example Find electric field 30

Important Example 31

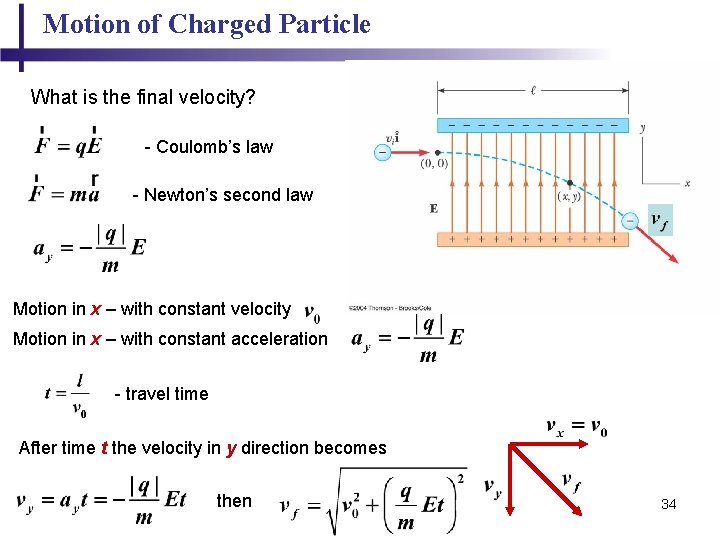
Motion of Charged Particle 32

Motion of Charged Particle • When a charged particle is placed in an electric field, it experiences an electrical force • If this is the only force on the particle, it must be the net force • The net force will cause the particle to accelerate according to Newton’s second law - Coulomb’s law - Newton’s second law 33

Motion of Charged Particle What is the final velocity? - Coulomb’s law - Newton’s second law Motion in x – with constant velocity Motion in x – with constant acceleration - travel time After time t the velocity in y direction becomes then 34