Chapter 25 SingleSource Shortest Paths Problem Definition Shortest

Chapter 25 Single-Source Shortest Paths • • Problem Definition Shortest paths and Relaxation Bellman-Ford algorithm Dijkstra’s algorithm 1/5/2022 chapter 25 1

Problem Definition: • Real problem: A motorist wishes to find the shortest possible route from Chicago to Boston. Given a road map of the United States on which the distance between each pair of adjacent intersections is marked, how can we determine this shortest route? • Formal definition: Given a graph G=(V, E, W), where each edge has a weight, find a shortest path from s to v for some interesting vertices s and v. • s—source • s—destination. 1/5/2022 chapter 25 2

• Simple but stupid solution: • we enumerate all the routes from Chicago to Boston, add up the distances on each route, and select the shortest. • It is easy to see, however, that even if we disallow routes that contain cycles, there are millions of possibilities, most of which are simply not worth considering. 1/5/2022 chapter 25 3

Shortest path: • The weight of path p=<v 0, v 1, …, vk > is the sum of the weights of its constituent edges: • We define the shortest-path weight from u to v by if there is a path from u to v otherwise • A shortest path from vertex u to vertex v is then defined as any path p with weight w(p)=. 1/5/2022 chapter 25 4

Variants: • Single-destination/source shortest-paths problem – If we change the direction of each edge in the given graph, single-destination becomes single -source. • Single-pair shortest-path problem • All-pairs shortest-paths problem 1/5/2022 chapter 25 5

Negative-Weight edges: • Edge weight may be negative. • negative-weight cycles– the total weight in the cycle (circuit) is negative. • If no negative-weight cycles reachable from the source s, then for all v V, the shortest-path weight remains well defined, even if it has a negative value. • If there is a negative-weight cycle on some path from s to v, we define =-. 1/5/2022 chapter 25 6

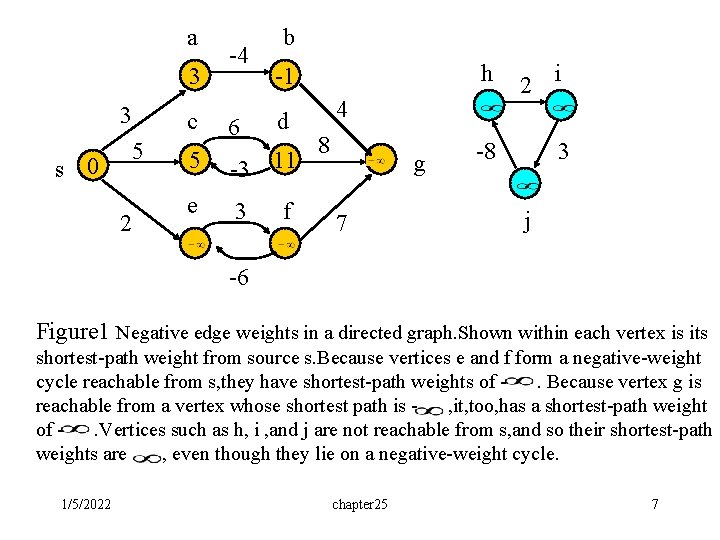
a 3 3 5 s 0 2 -4 b h -1 c d 6 5 -3 11 e 3 f 4 8 g 7 2 i -8 3 j -6 Figure 1 Negative edge weights in a directed graph. Shown within each vertex is its shortest-path weight from source s. Because vertices e and f form a negative-weight cycle reachable from s, they have shortest-path weights of. Because vertex g is reachable from a vertex whose shortest path is , it, too, has a shortest-path weight of. Vertices such as h, i , and j are not reachable from s, and so their shortest-path weights are , even though they lie on a negative-weight cycle. 1/5/2022 chapter 25 7

Representing shortest paths: • we maintain for each vertex v V , a predecessor [ v] that is the vertex in the shortest path right before v. • With the values of , a backtracking process can give the shortest path. (We will discuss that after the algorithm is given) 1/5/2022 chapter 25 8

Optimal substructure of a shortest path: • Lemma 25. 1 (basic) Subpaths of shortest paths are shortest paths Let p= <v 1, v 2, …, vk> be a shortest path from vertex v 1 to vertex vk and, for any i and j such that 1 i j k, let pij=<vi, vi+1, …, vj> be the subpath of p from vertex vi to vj. Then, pij is a shortest path from vi to vj. v 1 … vi … vj … vk 1/5/2022 chapter 25 9

Continue: • Corollary 25. 2 (basic) • Suppose that a shortest path p from a source s to a vertex v can be decomposed into s u v for some vertex u and path p’. Then, the weight of a shortest path from s to v is. 1/5/2022 chapter 25 10

Continue: • Lemma 25. 3 (basic) • Let G=(V, E) be a weighted, directed graph with weight function w: E R and source vertex s. Then, for all edges (u, v) E, we have. 1/5/2022 chapter 25 11

Initialization: • For each vertex v V, d[v] denotes an upper bound on the weight of a shortest path from source s to v. • d[v]– will be (s, v) after the execution of the algorithm. • initialize d[v] and [v] as follows: . • INITIALIZE-SINGLE-SOURCE(G, s) • for each vertex v V[G] • do d[v] • [v] NIL • d[s] 0 1/5/2022 chapter 25 12

Relaxation: • The process of relaxing an edge (u, v) consists of testing whether we can improve the shortest path to v found so far by going through u and, if so, updating d[v] and [v]. • RELAX(u, v, w) • if d[v]>d[u]+w(u, v) • then d[v] d[u]+w(u, v) (based on Lemma 25. 3) • [v] u 1/5/2022 chapter 25 13

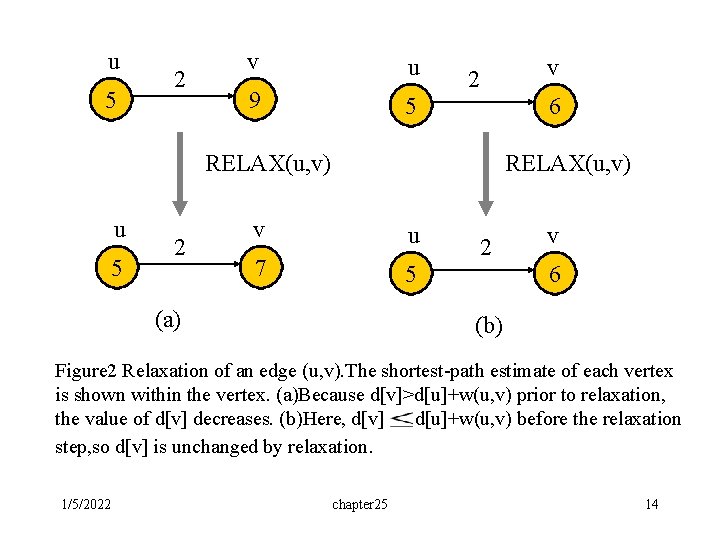
u 5 2 v u 9 5 v 2 6 RELAX(u, v) u 5 2 RELAX(u, v) v u 7 5 (a) 2 v 6 (b) Figure 2 Relaxation of an edge (u, v). The shortest-path estimate of each vertex is shown within the vertex. (a)Because d[v]>d[u]+w(u, v) prior to relaxation, the value of d[v] decreases. (b)Here, d[v] d[u]+w(u, v) before the relaxation step, so d[v] is unchanged by relaxation. 1/5/2022 chapter 25 14

Properties of relaxation: • Lemma 25. 4 (easy) • Let G=(G, E) be a weighted, directed graph with weight function w: E R, and let (u, v) E. Then, immediately after relaxing edge (u, v) by executing RELAX(u, v, w), we have d[v] d[u]+w(u, v). 1/5/2022 chapter 25 15

Continue: • Lemma 25. 5 (easy) • Let G=(V, E) be a weighted, directed graph with weight function w: E R. Let s V be the source vertex, and let the graph be initialized by INITIALIZE-SINGLE-SOURCE(G, s). Then, for all v V, and this invariant is maintained over any sequence of relaxation steps on edges of G. Moreover, once d[v] achieves its lower bound , it never changes. 1/5/2022 chapter 25 16

Continue: Corollary 25. 6 If no path connects a source vertex s V to a given vertex v V, then d[v]= . • Reasons: • After the graph is initialized by INITIALIZE- SINGLE-SOURCE(G, s), we have d[v]= (s, v)=. • This equality is maintained as invariant over any sequence of relaxation steps on the edges of G. 1/5/2022 chapter 25 17

Dijkstra’s Algorithm: • Dijkstra’s algorithm assumes that the weight for each edge is nonnegative. • maintains a set S of vertices such that – Every vertex v S, d[v]= (s, v), i. e. , the shortest-path from s to v has been found. • repeatedly selects the vertex u V-S such that d[u]=min {d[x]|x S}. (d[u] is the smallest for vertex in S) • a priority queue Q store vertices in V-S, keyed by their d[] values. • the graph G is represented by adjacency lists. 1/5/2022 chapter 25 18

Continue: • • • DIJKSTRA(G, w, s): INITIALIZE-SINGLE-SOURCE(G, s) S Q V[G] while Q do u EXTRACT -MIN(Q) S S {u} for each vertex v Adj[u] do RELAX(u, v, w) 1/5/2022 chapter 25 19

Example: • The execution of Dijkstra’s algorithm. The source is the leftmost vertex. d[] values are shown within the vertices, and shaded edges indicate predecessor values: • if edge (u, v) is shaded, then [v]=u. • Red vertices are in the set S, and white vertices are in the priority queue Q=V-S. (a) The situation just before the first iteration of the while loop. The shaded vertex has the minimum d value and is chosen as vertex u. (b)-(f) The situation after each successive iteration of the while loop. The shaded vertex in each part is chosen as vertex u of the next iteration. The d and values shown in part (f) are the final values. 1/5/2022 chapter 25 20

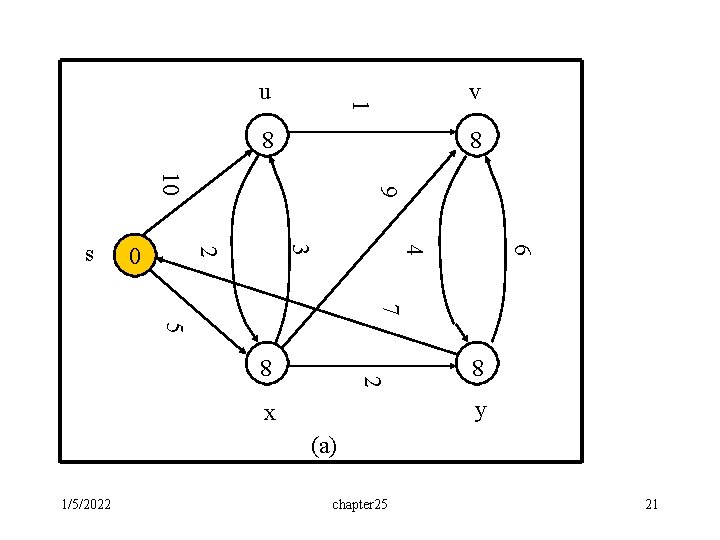
v 1 u 8 6 8 4 3 2 0 9 10 s 7 5 8 8 2 y x (a) 1/5/2022 chapter 25 21

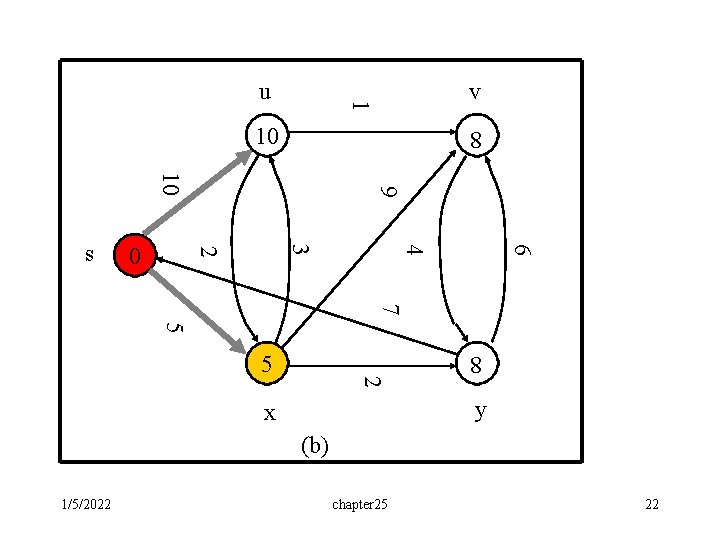
v 1 u 10 8 6 4 3 2 0 9 10 s 7 5 8 2 5 y x (b) 1/5/2022 chapter 25 22

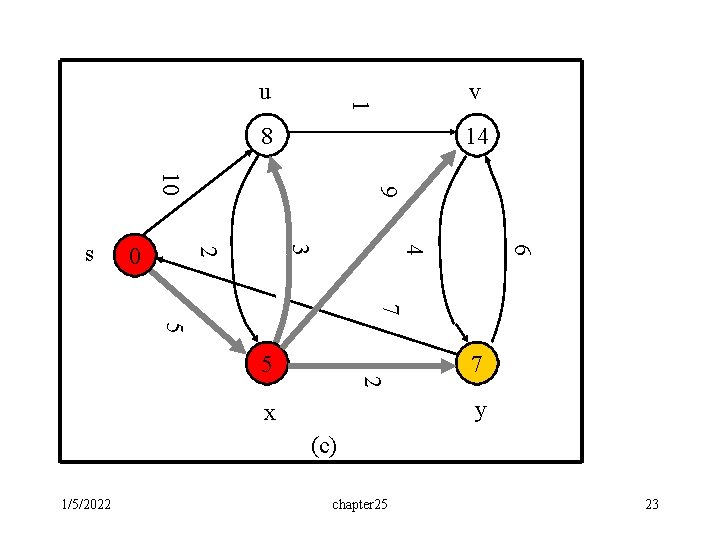
v 1 u 8 14 6 4 3 2 0 9 10 s 7 5 2 5 7 y x (c) 1/5/2022 chapter 25 23

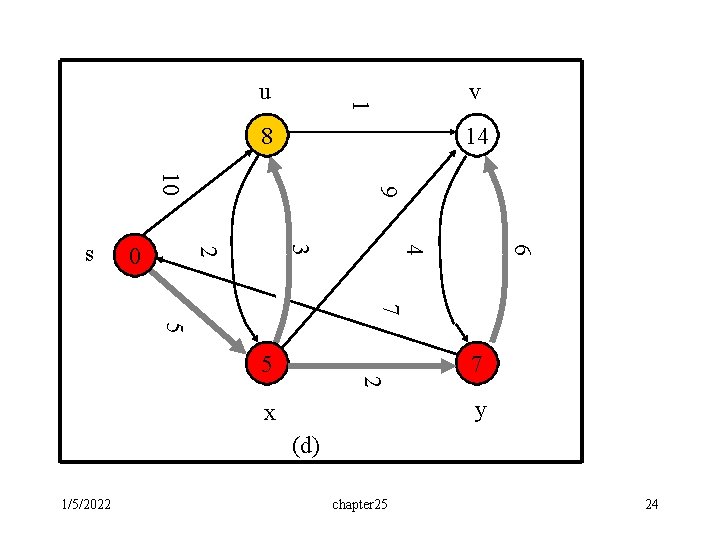
v 1 u 8 14 6 4 3 2 0 9 10 s 7 5 2 5 7 y x (d) 1/5/2022 chapter 25 24

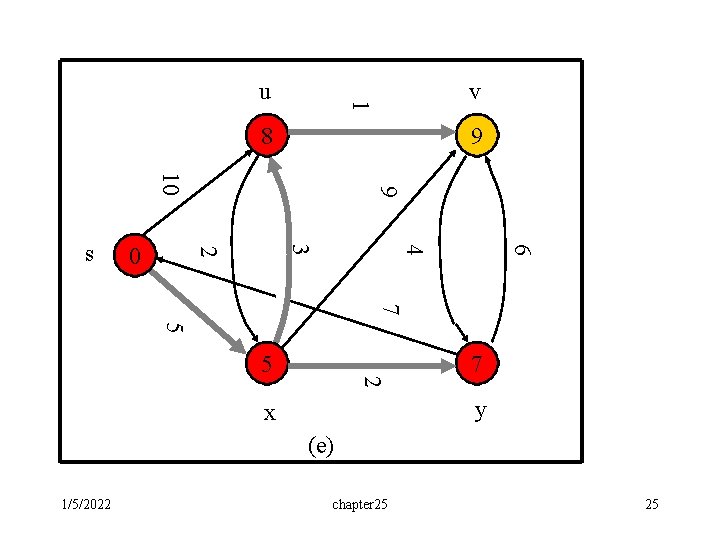
v 1 u 8 9 6 4 3 2 0 9 10 s 7 5 2 5 7 y x (e) 1/5/2022 chapter 25 25

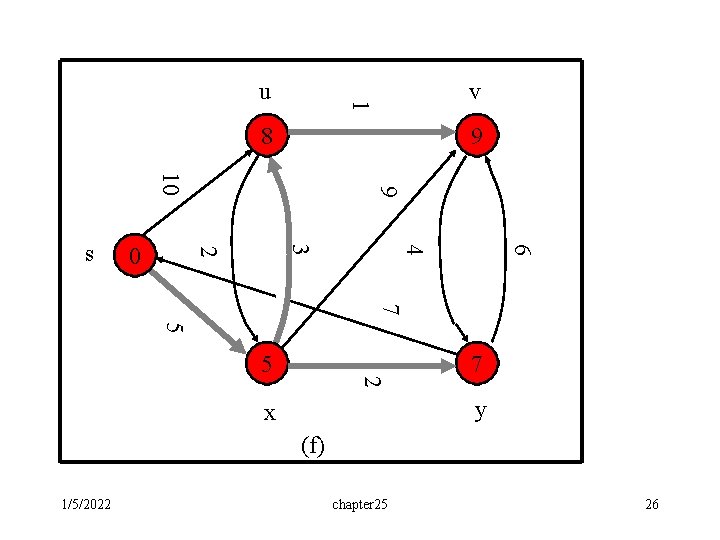
v 1 u 8 9 6 4 3 2 0 9 10 s 7 5 2 5 7 y x (f) 1/5/2022 chapter 25 26

Time complexity of Dijkstra’s Algorithm: • Time complexity depends on implementation of the Queue. • Implementation 1: Use an array to story the Queue • EXTRACT -MIN(Q) --takes O(|V|) time. – Totally, there are |V| EXTRACT -MIN(Q)’s. – time for |V| EXTRACT -MIN(Q)’s is O(|V|2). • RELAX(u, v, w) --takes O(1) time. – Totally |E| RELAX(u, v, w)’s are required. – time for |E| RELAX(u, v, w)’s is O(|E|). • Total time required is O(|V|2+|E|)=O(|V|2) 1/5/2022 chapter 25 27

Bellman-Ford algorithm: • The Bellman-Ford algorithm solves the single-source shortest-paths problem in the more general case in which edge weights can be negative. 1/5/2022 chapter 25 28

Continue: • • • BELLMAN-FORD(G, w, s): INITIALIZE-SINGLE-SOURCE(G, s) for i 1 to -1 do for each edge (u, v) E[G] do RELAX(u, v, w) for each edge (u, v) E[G] do if d[v]>d[u]+w(u, v) then return FALSE return TRUE 1/5/2022 chapter 25 29

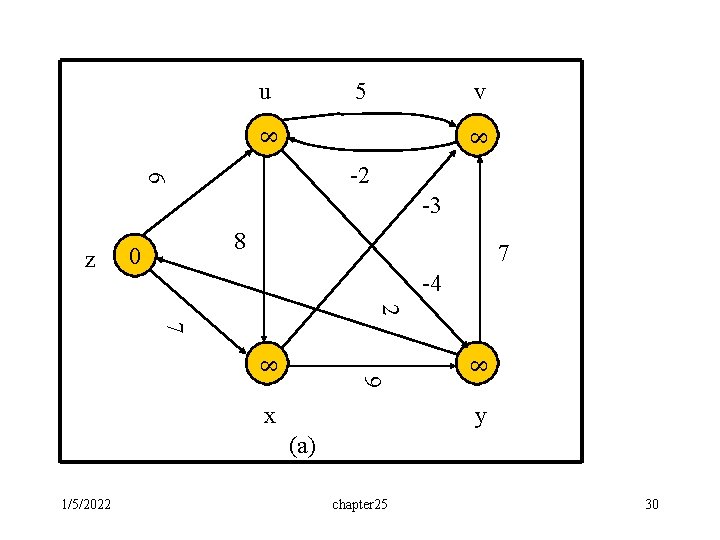
u 5 v 8 8 6 -2 -3 z 8 0 7 -4 2 7 8 8 9 x y (a) 1/5/2022 chapter 25 30

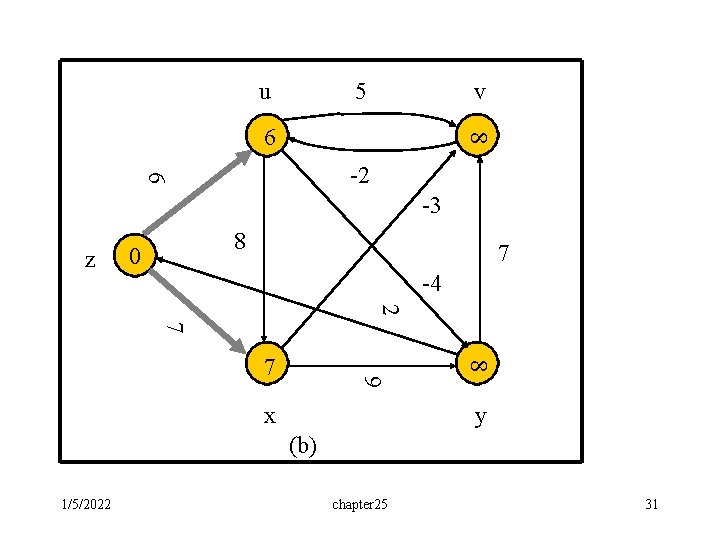
u 5 v 8 6 6 -2 -3 z 8 0 7 -4 2 7 8 7 9 x y (b) 1/5/2022 chapter 25 31

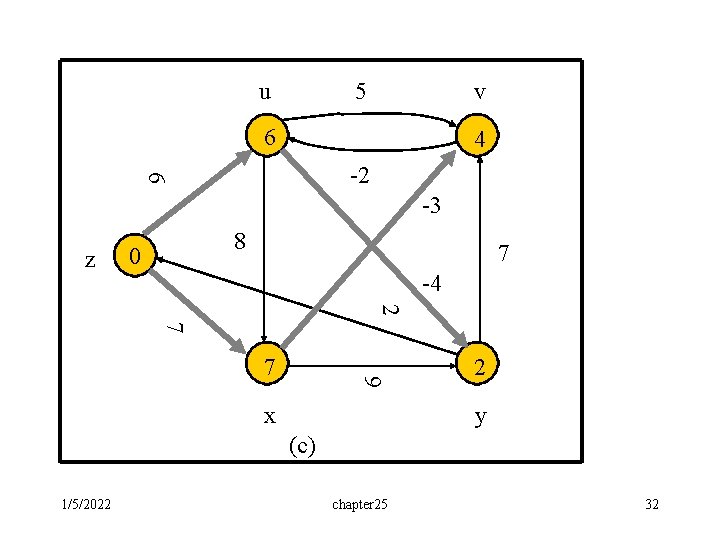
u 5 v 6 4 6 -2 -3 z 8 0 7 -4 2 7 9 7 x 2 y (c) 1/5/2022 chapter 25 32

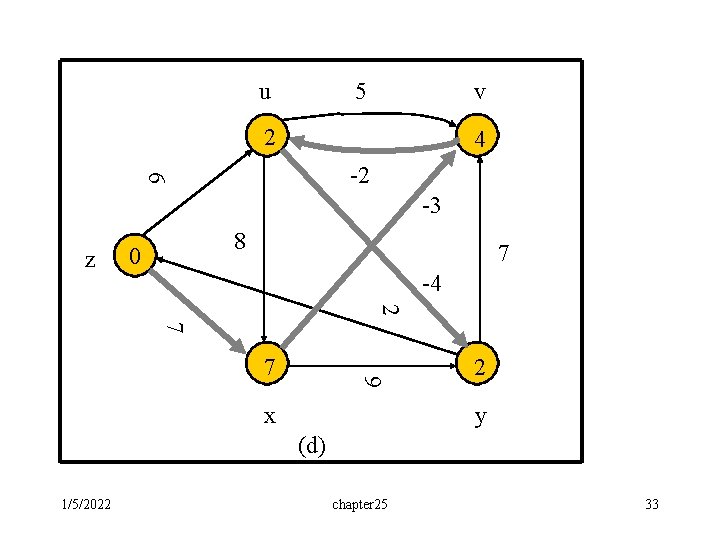
u 5 v 2 4 6 -2 -3 z 8 0 7 -4 2 7 9 7 x 2 y (d) 1/5/2022 chapter 25 33

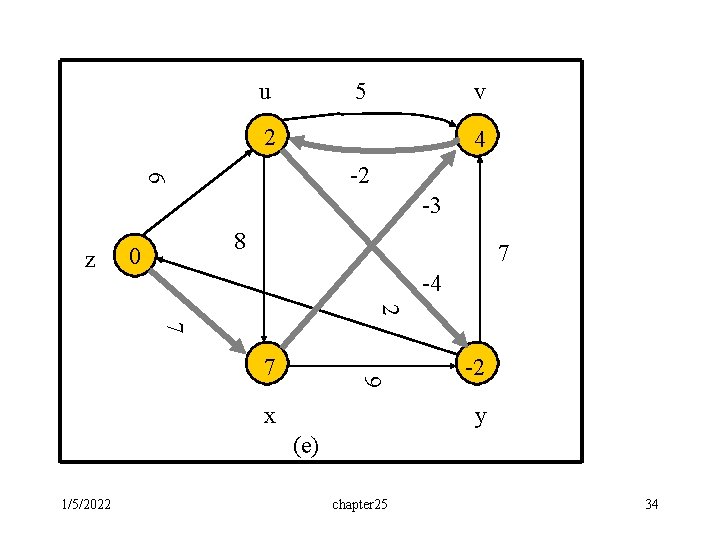
u 5 v 2 4 6 -2 -3 z 8 0 7 -4 2 7 9 7 x -2 y (e) 1/5/2022 chapter 25 34

The End: • Have a nice day. 1/5/2022 chapter 25 35