Chapter 25 Allpairs shortest paths Contents Usingle source

Chapter 25. All-pairs shortest paths

Contents Usingle source shortest path algorithms Presents O(V 4)-time algorithm, O(V 3 log. V)-time algorithm, O(V 3)-time algorithm O(V 4)-time algorithm O(V 3 log V)- time algorithm Floyd-Warshall algorithm Transitive closure of a directed graph

Usingle source shortest path algorithms Positive edges Negative edges

Usingle source shortest path algorithms We can solve an all-pairs shortest-paths problem by running a single-source shortest-paths algorithm |V| times, once for each vertex as the source.

Usingle source shortest path algorithms Positive edges Using dijkstra algorithm: The linear-array implementation The binary min-heap implementation O(V E lg V), Fibonacci heap O(V 2 lg V + V E). O(V 3 + V E) = O(V 3).

Usingle source shortest path algorithms Negative edges Using Bellman-Ford algorithm: O(V 2 E) dense graph O(V 4)

Use adjacency matrix Predecessor matrix

Use adjacency matrix We assume that the vertices are numbered 1, 2, . . . , |V| The input is an n×n matrix W representing the edge weights of an n-vertex directed graph G = (V, E) Negative-weight edges are allowed, but we assume for the time being that the input graph contains no negative-weight cycles.

Predecessor matrix say Π = (πij) πij = NIL if either i = j or there is not path from i to j. πij is the predecessor of j on some shortest path from i to j.

For each vertex i ∈ V, we define predecessor subgraph of G for i as Gπ, i = (Vπ, i, Eπ, i), where Vπ, i = {j ∈ V |πij = NIL} ∪ {i} Eπ, i = {(πij, j)|j ∈ Vπ, i − {i}} If Gπ, i is a shortest-paths tree, then PRINTALLPAIRS-SHORTEST-PATH will print a shortest path from i to j.

PRINT-ALL-PAIRS-SHORTEST-PATH(Π, i, j) 1 if i = j 2 then print i 3 else if πij = NIL 4 then print “no path from” i “to” j “exists” 5 else PRINT-ALL-PAIRS-SHORTEST-PATH(Π, i, πij) 6 print j

25. 1 Shortest paths and matrix multiplication O(V 4)-time algorithm use dynamic programming use matrix multiplication associative (short explanation) computing predecessor matrix

25. 1 Shortest paths and matrix multiplication use dynamic programming Characterize the structure of an optimal solution. Recursively define the value of an optimal solution. Compute the value of an optimal solution in a bottom-up fashion.

25. 1 Shortest paths and matrix multiplication The structure of a shortest path on a graph G = (V, E), all subpaths of a shortest path are shortest paths. (Lemma 24. 1) k P 2 P 1 i j P` : {1, 2, …, k-1} p′ is a shortest path from i to k, and so δ(i, j) = δ(i, k) + wkj.

25. 1 Shortest paths and matrix multiplication A recursive solution to the all-pairs shortest-paths problem Let be the minimum weight of any path from vertex i to vertex j that contains at most m edges When m = 0, then When m ≥ 1, then

25. 1 Shortest paths and matrix multiplication If the graph contains no negative-weight cycles, For every pair of vertices i and j for which δ(i, j) < ∞ there is a shortest path from i to j that is simple and thus contains at most n - 1 edges. A path from vertex i to vertex j with more than n - 1 edges cannot have lower weight than a shortest path from i to j. Therefore,

25. 1 Shortest paths and matrix multiplication Computing the shortest-path weights bottom up Input the matrix W = (wij), we now compute a series of matrices L(1), L(2), . . . , L(n-1), where for m = 1, 2, . . . , n - 1, we have. The final matrix L(n-1) contains the actual shortest-path weights. Observe that for all vertices i, j ∈ V , and so L(1) = Wij.

25. 1 Shortest paths and matrix multiplication Let L(m− 1) = L, L(m) = L. We have EXTEND-SHORTEST-PATHS(L, W) 1 n ← rows[L] 2 let be an n × n matrix 3 for i ← 1 to n 4 do for j ← to n 5 do 6 for k ← 1 to n 7 do 8 return L′ Costs Θ(n 3) time.

25. 1 Shortest paths and matrix multiplication 1 2 3 4 5 6 7 8 MATRIX-MULTIPLY(A, B) n ← rows[A] let C be an n × n matrix for i ← 1 to n do for j ← 1 to n do cij ← 0 for k ← 1 to n do cij ← cij + aik · bkj return C

25. 1 Shortest paths and matrix multiplication 1 2 3 4 5 SLOW-ALL-PAIRS-SHORTEST-PATHS(W) n ← rows[W] L(1) ←W for m ← 2 to n − 1 do L(m) ← EXTEND-SHORTEST-PATHS(L(m− 1), W) return L(n− 1) costs Θ(n 4) time.

25. 1 Shortest paths and matrix multiplication Improving the running time we are interested only in matrix L(n-1). Recall that in the absence of negative-weight cycles, implies L(m) = L(n-1) for all integers m ≥ n - 1. Therefore, we can compute L(n-1) with only �lg(n - 1)� matrix products by computing the sequence

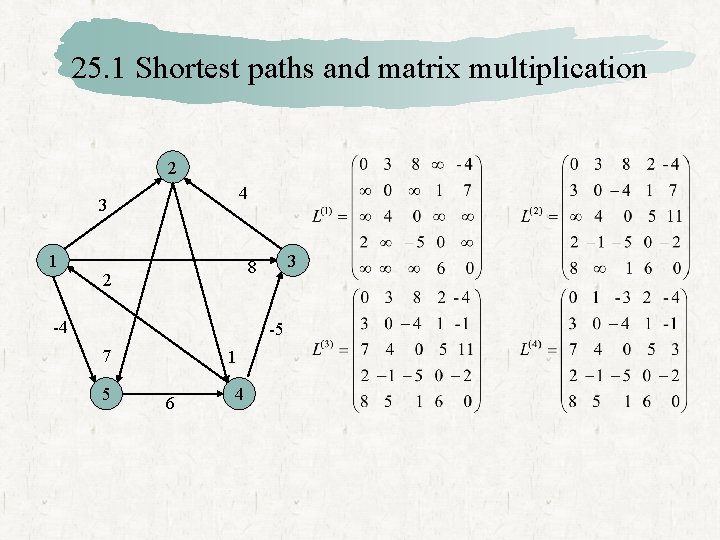
25. 1 Shortest paths and matrix multiplication 2 4 3 1 3 8 2 -4 -5 7 5 1 6 4

25. 1 Shortest paths and matrix multiplication

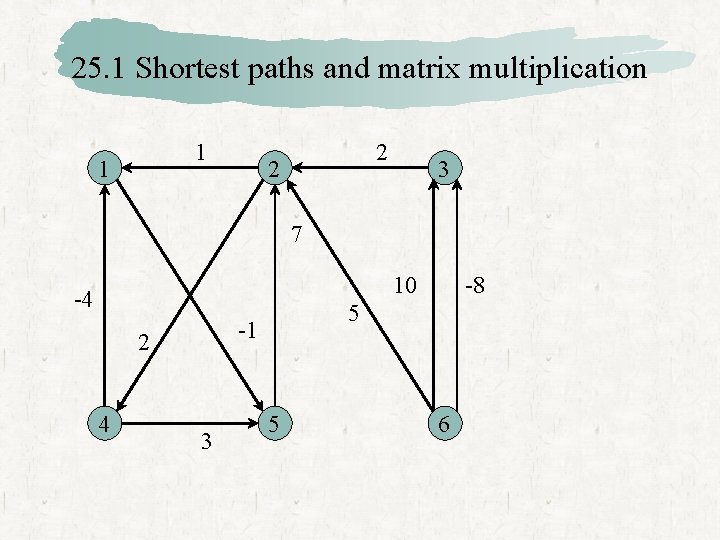
25. 1 Shortest paths and matrix multiplication 1 1 2 2 3 7 10 -4 4 5 -1 2 3 -8 5 6

25. 1 Shortest paths and matrix multiplication 1 2 3 4 5 6 7 FASTER-ALL-PAIRS-SHORTEST-PATHS(W) n ← rows[W] L(1) ← W m← 1 while m < n - 1 do L(2 m) ← EXTEND-SHORTEST-PATHS(L(m), L(m)) m ← 2 m return L(m) Costs Θ(n 3) time.

25. 2 The Floyd-Warshall algorithm Intermediate Vertex An intermediate vertex of a simple path p = <v 1, v 2, · · · , vl> is any vertex of p other than v 1 and vl.

25. 2 The Floyd-Warshall algorithm The structure of a shortest path Floyd-Warshall algorithm is based on the observation of the intermediate vertices, which costs Θ(|V |3) time. Let V = {1, 2, · · · , n}. For any pair of vertices i, j ∈ V , consider all paths from i to j whose intermediate vertices are all drawn from {1, 2, · · · , k}, and let p be a minimum weight path from among them.

25. 2 The Floyd-Warshall algorithm If k is not an intermediate vertex of path p, then all intermediate vertices of p are in {1, 2, · · · , k − 1}. If k is an intermediate vertex of path p, then we break p down into all intermediate vertices in {1, 2. . , k-1} k P 1 P 2 i j P : all intermediate vertices in {1, 2, …, k-1}

25. 2 The Floyd-Warshall algorithm A recursive solution to the all-pairs shortest-paths problem Let be the weight of a shortest path from vertex i to vertex j for which all intermediate vertices are in the set {1, 2, · · · , k}. We have the following recurrence: Because for any path, all intermediate vertices are in the set {1, 2, · · · , n}, the matrix gives the final answer: for all i, j ∈ V.

25. 2 The Floyd-Warshall algorithm FLOYD-WARSHALL(W) 1 n ← rows[W] 2 D(0) ←W 3 for k ← 1 to n 4 do for i ← 1 to n 5 do for j ← 1 to n 6 do 7 return D(n) costs Θ(n 3) time.

25. 2 The Floyd-Warshall algorithm

25. 2 The Floyd-Warshall algorithm

25. 2 The Floyd-Warshall algorithm

25. 2 The Floyd-Warshall algorithm Constructing A Shortest Path Let be the predecessor of vertex j on a shortest path from vertex i with all intermediate vertices in {1, 2, · · · , k}.

25. 2 The Floyd-Warshall algorithm Transitive Closure of Graph Given a directed graph G = (V, E) with vertex set V = {1, 2, · · · , n}. The transitive closure of G is defined as the graph G∗ = (V, E∗), where E∗ = {(i, j) : there is a path from vertex i to vertex j in G}.