Chapter 24 SingleSource Shortest Paths Input Directed graph

Chapter 24: Single-Source Shortest Paths Input: - Directed graph G(V, E). - Weight (‘length’) function w: E R. Notions: - Weight/length of a directed path. - Shortest path from u to v, denoted δ(u, v): length of minimum weight/length path from u to v. Other variants: - Single-source shortest paths - All-pair shortest paths

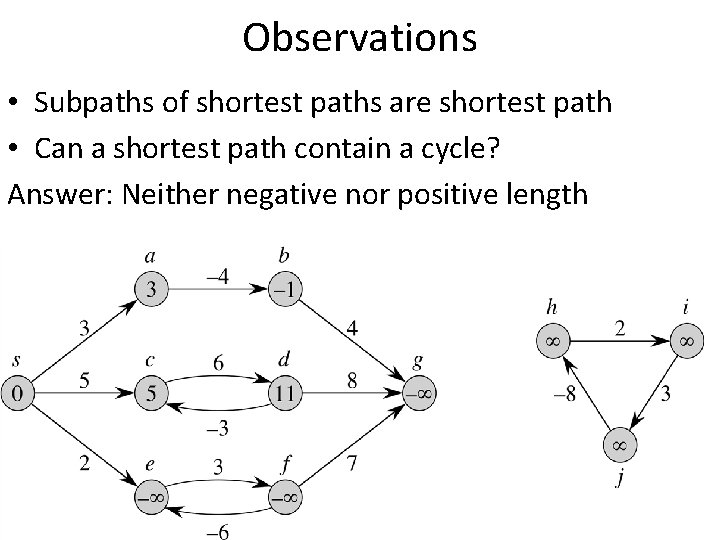
Observations • Subpaths of shortest paths are shortest path • Can a shortest path contain a cycle? Answer: Neither negative nor positive length

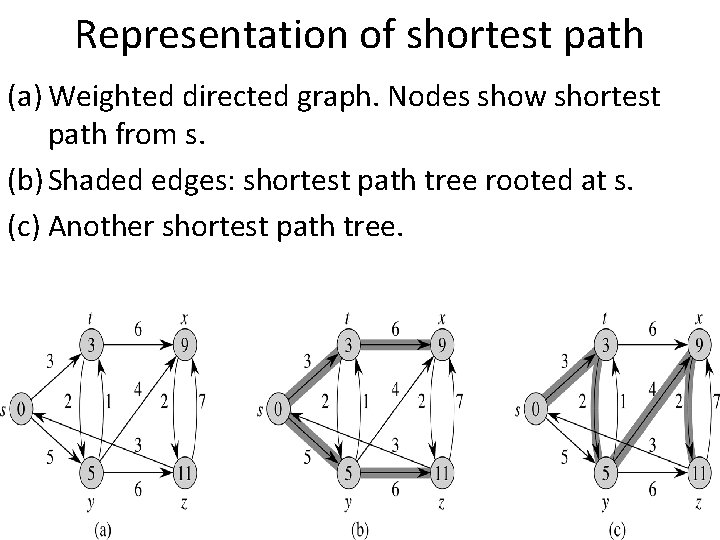
Representation of shortest path (a) Weighted directed graph. Nodes show shortest path from s. (b) Shaded edges: shortest path tree rooted at s. (c) Another shortest path tree.

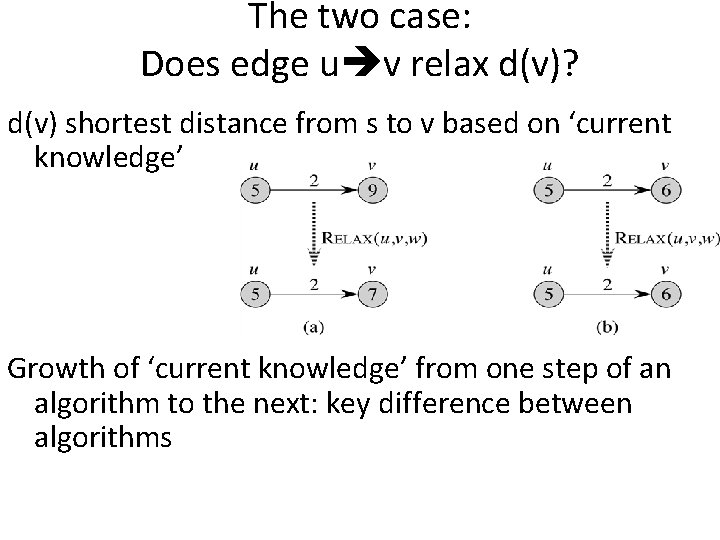
The two case: Does edge u v relax d(v)? d(v) shortest distance from s to v based on ‘current knowledge’ Growth of ‘current knowledge’ from one step of an algorithm to the next: key difference between algorithms

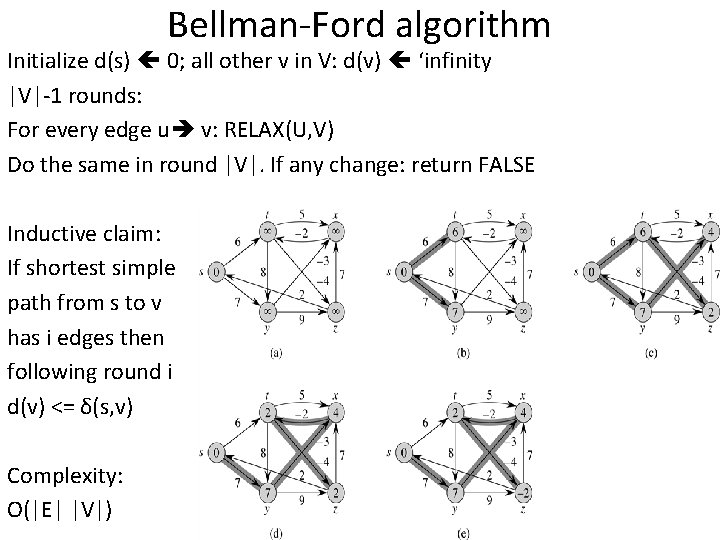
Bellman-Ford algorithm Initialize d(s) 0; all other v in V: d(v) ‘infinity |V|-1 rounds: For every edge u v: RELAX(U, V) Do the same in round |V|. If any change: return FALSE Inductive claim: If shortest simple path from s to v has i edges then following round i d(v) <= δ(s, v) Complexity: O(|E| |V|)

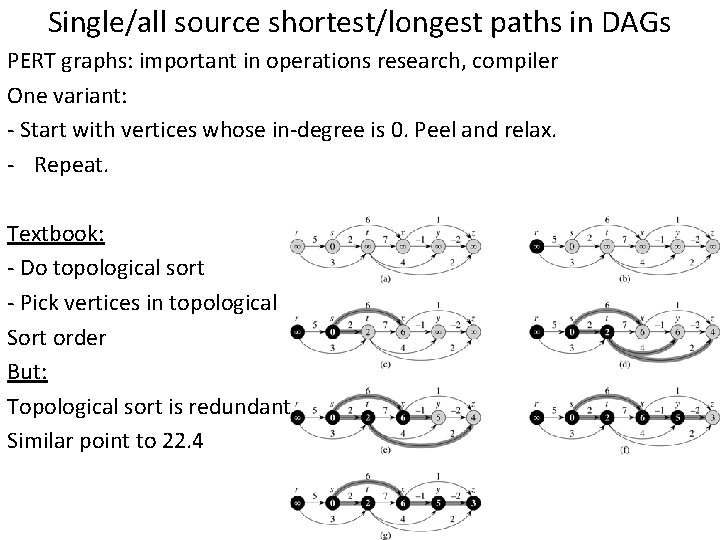
Single/all source shortest/longest paths in DAGs PERT graphs: important in operations research, compiler One variant: - Start with vertices whose in-degree is 0. Peel and relax. - Repeat. Textbook: - Do topological sort - Pick vertices in topological Sort order But: Topological sort is redundant. Similar point to 22. 4

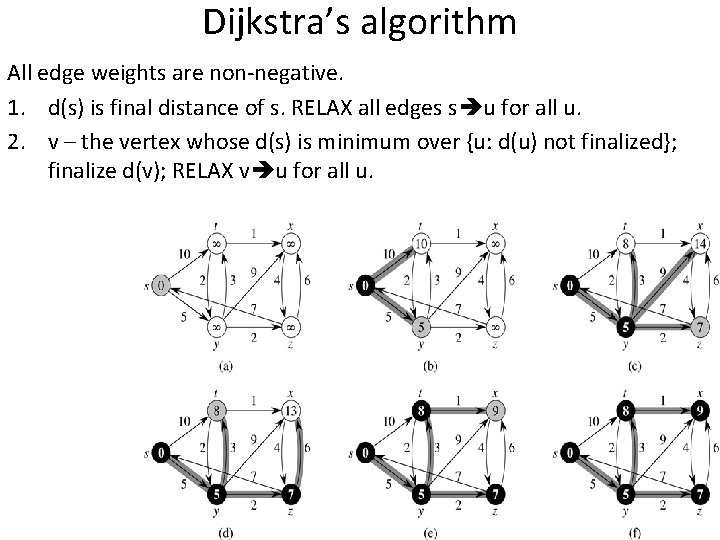
Dijkstra’s algorithm All edge weights are non-negative. 1. d(s) is final distance of s. RELAX all edges s u for all u. 2. v – the vertex whose d(s) is minimum over {u: d(u) not finalized}; finalize d(v); RELAX v u for all u.

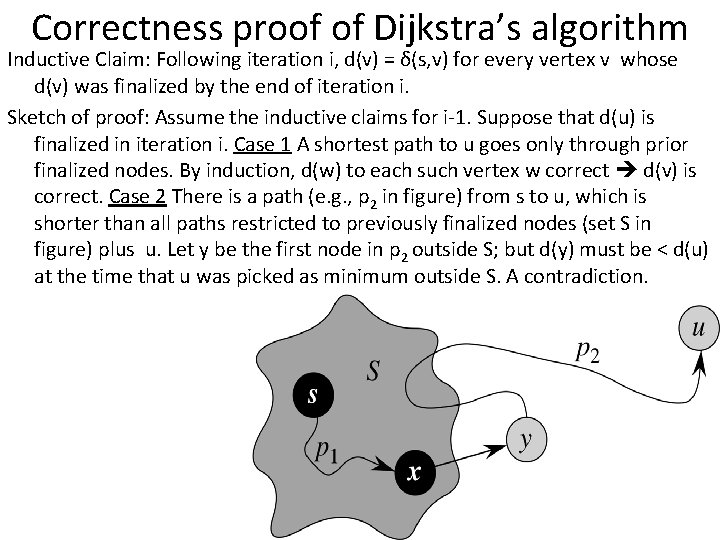
Correctness proof of Dijkstra’s algorithm Inductive Claim: Following iteration i, d(v) = δ(s, v) for every vertex v whose d(v) was finalized by the end of iteration i. Sketch of proof: Assume the inductive claims for i-1. Suppose that d(u) is finalized in iteration i. Case 1 A shortest path to u goes only through prior finalized nodes. By induction, d(w) to each such vertex w correct d(v) is correct. Case 2 There is a path (e. g. , p 2 in figure) from s to u, which is shorter than all paths restricted to previously finalized nodes (set S in figure) plus u. Let y be the first node in p 2 outside S; but d(y) must be < d(u) at the time that u was picked as minimum outside S. A contradiction.

Complexity of Dijktra’s algorithm O(|E|) DECREASE-KEY queries and O(|V|) EXTRACTMIN queries lead to O((|E|+|V|) log |V|) time. Can be improved to to O(|E|+|V| log |V|) time.