Chapter 24 Classical Theory of Electromagnetic Radiation A

Chapter 24 Classical Theory of Electromagnetic Radiation

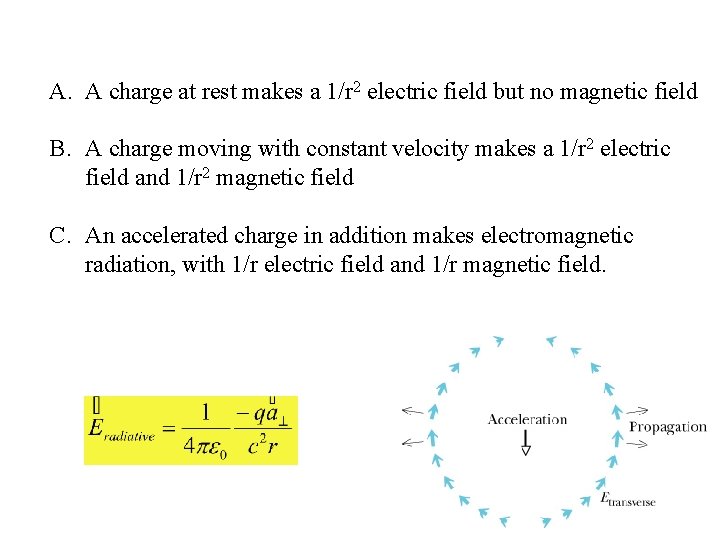
A. A charge at rest makes a 1/r 2 electric field but no magnetic field B. A charge moving with constant velocity makes a 1/r 2 electric field and 1/r 2 magnetic field C. An accelerated charge in addition makes electromagnetic radiation, with 1/r electric field and 1/r magnetic field.

Question A narrow collimated pulse of radiation propagates in the -x direction. There is an electron at location A. What is the direction of the radiative electric field observed at location B? A e- D B C

Stability of Atoms Circular motion: Is there radiation emitted? Classical physics says “YES” Þ orbiting particle must lose energy! Þ speed decreases Þ particle comes closer to center Classical model of atom: Electrons should fall on nucleus! To explain the facts - introduction of quantum mechanics: Electrons can move around certain orbits only and emit E/M radiation only when jumping from one orbit to another v a

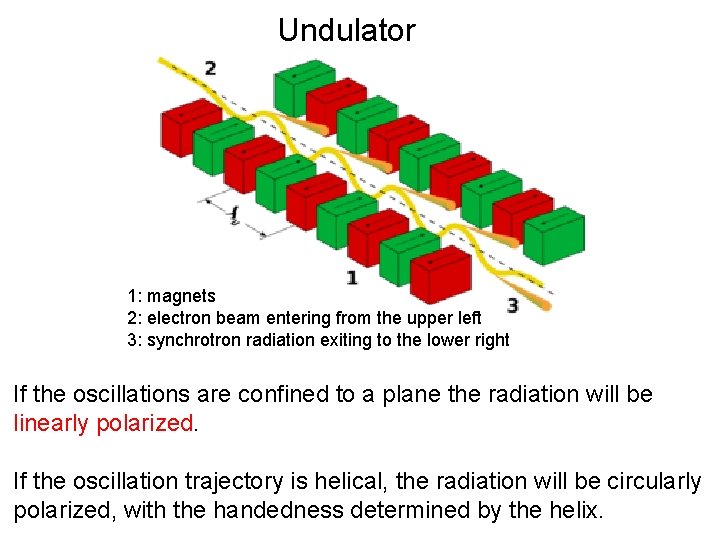
Undulator 1: magnets 2: electron beam entering from the upper left 3: synchrotron radiation exiting to the lower right If the oscillations are confined to a plane the radiation will be linearly polarized. If the oscillation trajectory is helical, the radiation will be circularly polarized, with the handedness determined by the helix.

History Accelerator-based synchrotron light was seen for the first time at the General Electric Research Laboratory in the USA in 1947 in a type of accelerator known as a synchrotron. First considered a nuisance because it caused the particles to lose energy, it recognized in the 1960 s as light with exceptional properties. Simply trillion times brighter than the beam produced by a hospital x-ray machine. Looking head on into the upper and lower rows of magnets (jaws) in an undulator. The adjustable vertical distance between the jaws determines the wavelength emitted. Here, a laser is used to simulate the burst of light produced. (Courtesy: Advanced Light Source)

Argonne National Laboratory, USA

Sinusoidal Electromagnetic Radiation Acceleration: Sinusoidal E/M field

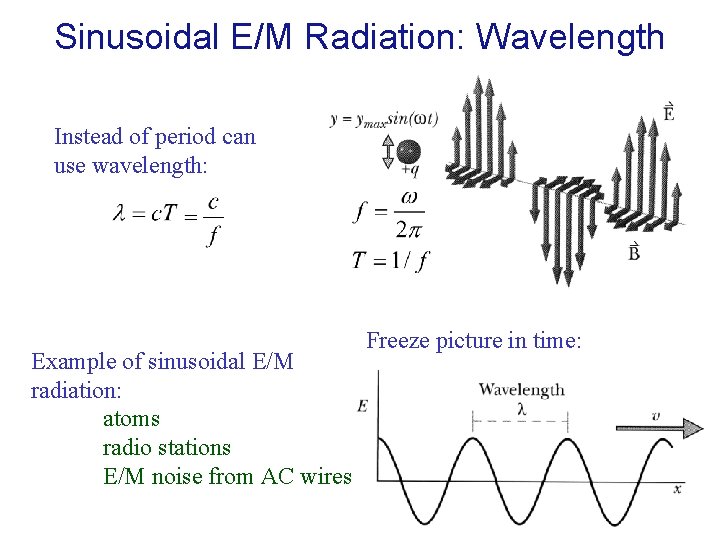
Sinusoidal E/M Radiation: Wavelength Instead of period can use wavelength: Example of sinusoidal E/M radiation: atoms radio stations E/M noise from AC wires Freeze picture in time:

Energy and Momentum of E/M Radiation According to particle theory of light: photons have energy and momentum Classical E/M model of light: E/M radiation must carry energy and momentum

Energy of E/M Radiation A particle will experience electric force during a short time d/c: What will happen to the ball? It will oscillate Energy was transferred from E/M field to the ball Amount of energy in the pulse is ~ E 2

Energy of E/M Radiation Ball gained energy: Pulse energy must decrease E/M radiation: E=c. B Energy density of magnetic field in a traveling wave is exactly the energy density of the electric field

Energy Flux There is E/M energy stored in the pulse: Pulse moves in space: there is energy flux Units: J/(m 2 s) = W/m 2 During t: used: E=c. B, 0 0=1/c 2

Energy Flux: The Poynting Vector The direction of the E/M radiation was given by Energy flux, the “Poynting vector”: John Henry Poynting (1852 -1914) • S is the rate of energy flux in E/M radiation • It points in the direction of the E/M radiation

Exercise A laser pointer emits ~5 m. W of light power. What is the approximate magnitude of the electric field? Solution: 1. Spot size: ~2 mm 2. flux = (5. 10 -3 W)/(3. 14. 0. 0012 m 2)=1592 W/m 2 3. Electric field: (rms value) What if we focus it into 2 a micron spot? Flux will increase 106 times, E will increase 103 times:

Momentum of E/M Radiation • E field starts motion, • No net momentum change in the y direction • Moving charge in magnetic field: y x Fmag What if there is negative charge? ‘Radiation pressure’: What is its magnitude? Average speed: v/2 Fmag

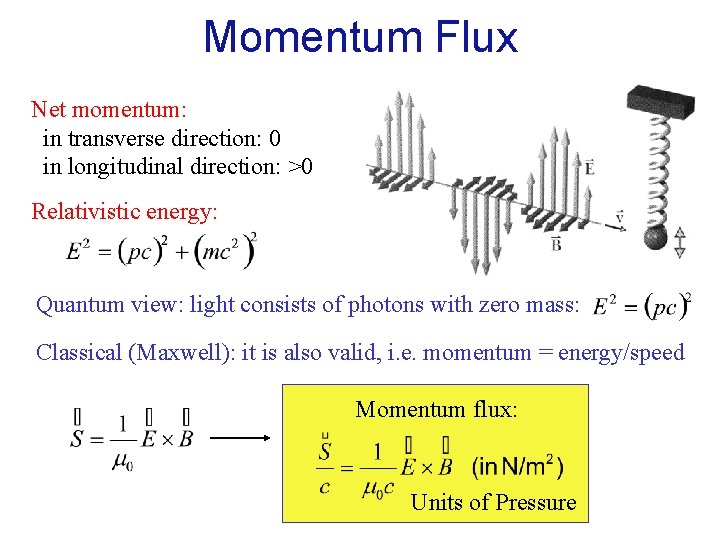
Momentum Flux Net momentum: in transverse direction: 0 in longitudinal direction: >0 Relativistic energy: Quantum view: light consists of photons with zero mass: Classical (Maxwell): it is also valid, i. e. momentum = energy/speed Momentum flux: Units of Pressure

Exercise: Solar Sail What is the force due to sun light on a sail with the area 1 km 2 near the Earth orbit (1400 W/m 2)? Solution: Note: What if we have a reflective surface? Total force on the sail: Atmospheric pressure is ~ 105 N/m 2

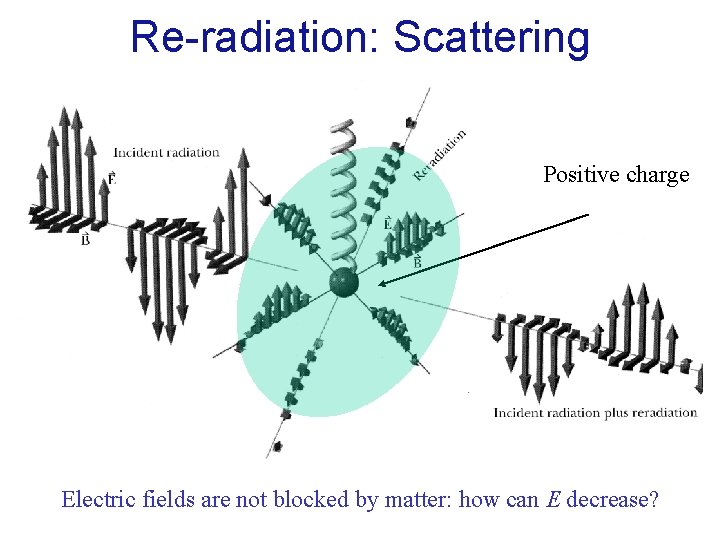
Re-radiation: Scattering Positive charge Electric fields are not blocked by matter: how can E decrease?

Cardboard Why there is no light going through a cardboard? Electric fields are not blocked by matter Electrons and nucleus in cardboard reradiate light Behind the cardboard reradiated E/M field cancels original field

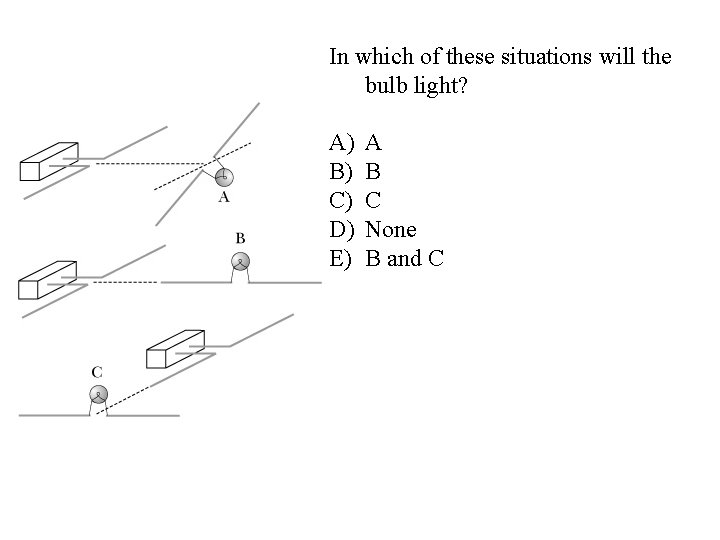
In which of these situations will the bulb light? A) B) C) D) E) A B C None B and C