Chapter 22 RC and LR Time Constants Topics

Chapter 22 RC and L/R Time Constants Topics Covered in Chapter 22 22 -1: Response of Resistance Alone 22 -2: L/R Time Constant 22 -3: High Voltage Produced by Opening an RL Circuit 22 -4: RC Time Constant 22 -5: RC Charge and Discharge Curves 22 -6: High Current Produced by Short-Circuiting RC Circuit © 2007 The Mc. Graw-Hill Companies, Inc. All rights reserved.

Topics Covered in Chapter 22 § 22 -7: RC Waveshapes § 22 -8: Long and Short Time Constants § 22 -9: Charge and Discharge with Short RC Time Constant § 22 -10: Long Time Constant for RC Coupling Circuit § 22 -11: Advanced Time Constant Analysis § 22 -12: Comparison of Reactance and Time Constant Mc. Graw-Hill © 2007 The Mc. Graw-Hill Companies, Inc. All rights reserved.

22 -1: Response of Resistance Alone § Resistance has only opposition to current. § There is no reaction to a change. § R has no concentrated magnetic field to oppose a change in I, like inductance, and no electric field to store charge that opposes a change in V, like capacitance.

22 -1: Response of Resistance Alone § When the switch S is closed in Fig. 22 -1 (a), the battery supplies 10 V across the 10 -Ω R and the resultant I is 1 A. § The graph in Fig. 22 -1 (b) shows that I changes from 0 to 1 A instantly when the switch is closed. Fig. 22 -1: Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

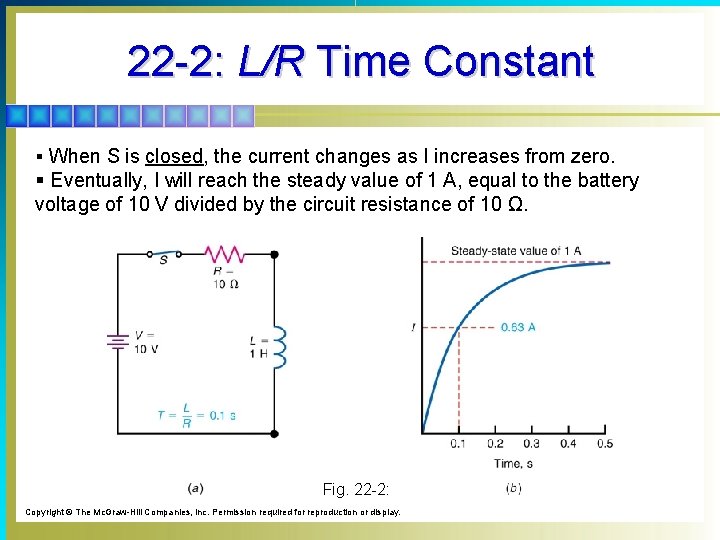
22 -2: L/R Time Constant § The action of an RL circuit during the time current builds up to a specific value is its transient response. § Transient response is a temporary condition that exists only until the steady-state current is reached. § The transient response is measured in terms of the ratio L/R, which is the time constant T of an inductive circuit. § T = L/R § The time constant is a measure of how long it takes the current to change by 63. 2%.

22 -2: L/R Time Constant § When S is closed, the current changes as I increases from zero. § Eventually, I will reach the steady value of 1 A, equal to the battery voltage of 10 V divided by the circuit resistance of 10 Ω. Fig. 22 -2: Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

22 -3: High Voltage Produced by Opening an RL Circuit § When an inductive circuit is opened, the time constant for current decay becomes very short because L/R becomes smaller with the high resistance of the open. § Then the current drops toward zero much faster than the rise of current when the switch is closed. § The result is a high value of self-induced voltage across a coil whenever an RL circuit is opened. § This high voltage can be much greater than the applied voltage.

22 -3: High Voltage Produced by Opening an RL Circuit § In Fig. 22 -3, the neon bulb requires 90 V for ionization, at which time it glows. § The source is only 8 V, but when the switch is opened, the self-induced voltage is high enough to light the bulb for an instant. §The sharp voltage pulse or spike is more than 90 V just after the switch is opened. Fig. 22 -3: Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

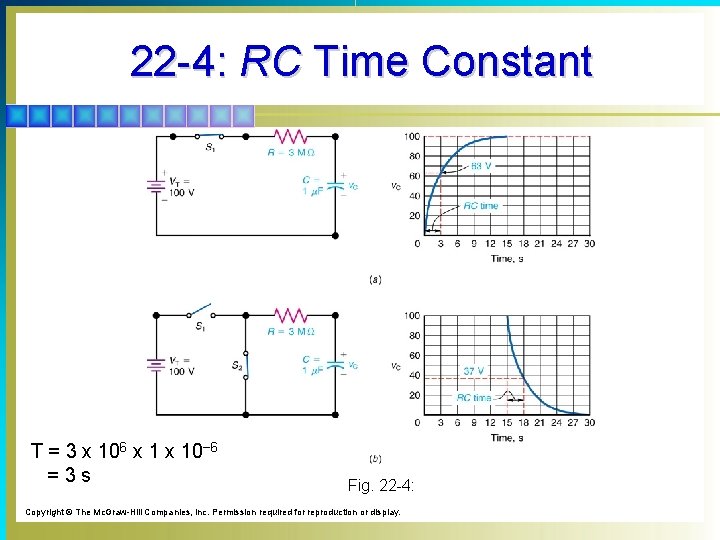
22 -4: RC Time Constant § The transient response of capacitive circuits is measured in terms of the product R x C. § To calculate the time constant, T=Rx. C where R is in ohms, C is in farads, and T is in seconds.

22 -4: RC Time Constant T = 3 x 106 x 10− 6 =3 s Fig. 22 -4: Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

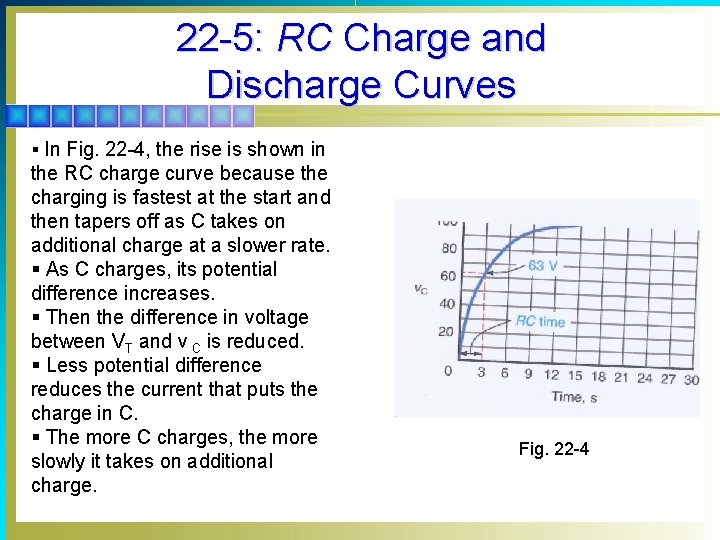
22 -5: RC Charge and Discharge Curves § In Fig. 22 -4, the rise is shown in the RC charge curve because the charging is fastest at the start and then tapers off as C takes on additional charge at a slower rate. § As C charges, its potential difference increases. § Then the difference in voltage between VT and v C is reduced. § Less potential difference reduces the current that puts the charge in C. § The more C charges, the more slowly it takes on additional charge. Fig. 22 -4

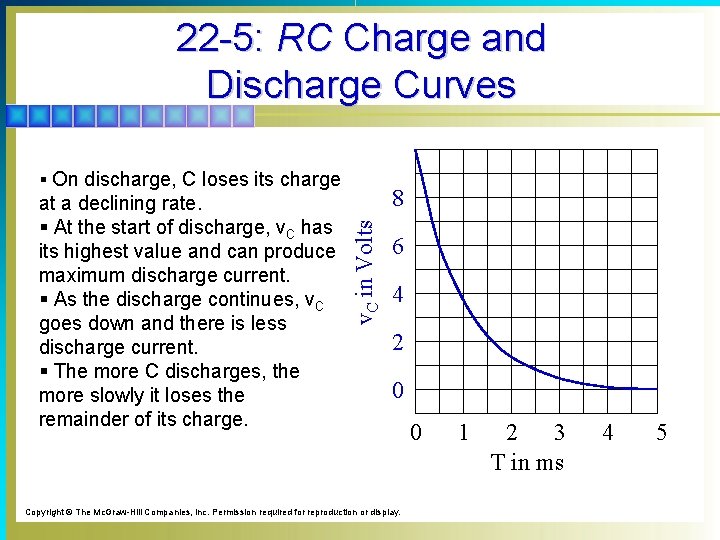
22 -5: RC Charge and Discharge Curves § On discharge, C loses its charge 8 v. C in Volts at a declining rate. § At the start of discharge, v. C has its highest value and can produce maximum discharge current. § As the discharge continues, v. C goes down and there is less discharge current. § The more C discharges, the more slowly it loses the remainder of its charge. 6 4 2 0 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. 0 1 2 3 T in ms 4 5

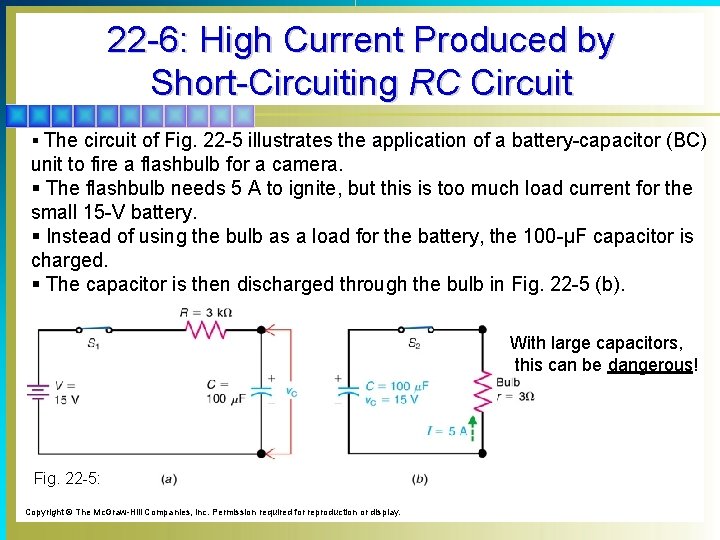
22 -6: High Current Produced by Short-Circuiting RC Circuit § A capacitor can be charged slowly by a small charging current through a high resistance and then be discharged quickly through a low resistance to obtain a momentary surge, or pulse of discharge current. § This idea corresponds to the pulse of high voltage obtained by opening an inductive circuit.

22 -6: High Current Produced by Short-Circuiting RC Circuit § The circuit of Fig. 22 -5 illustrates the application of a battery-capacitor (BC) unit to fire a flashbulb for a camera. § The flashbulb needs 5 A to ignite, but this is too much load current for the small 15 -V battery. § Instead of using the bulb as a load for the battery, the 100 -μF capacitor is charged. § The capacitor is then discharged through the bulb in Fig. 22 -5 (b). With large capacitors, this can be dangerous! Fig. 22 -5: Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

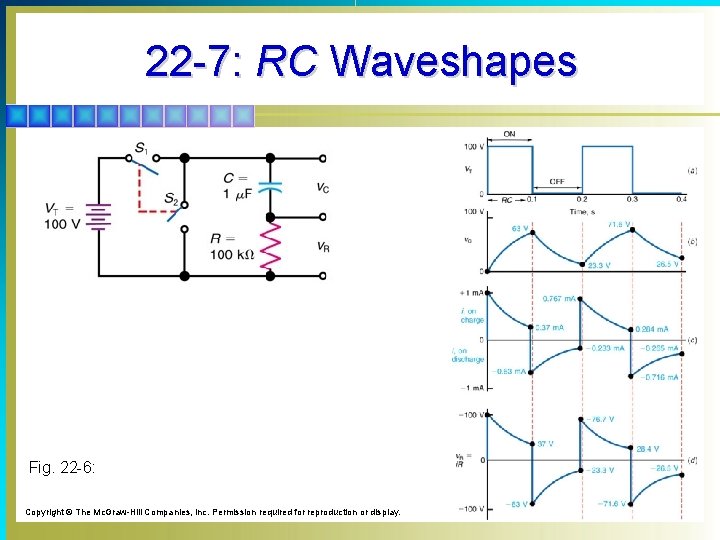
22 -7: RC Waveshapes § Voltage and current waveshapes in RC circuits can show when a capacitor is allowed to charge through a resistance for RC time and then discharge through the same resistance for the same amount of time. § Waveshapes show some useful details about the voltage and current for charging and discharging.

22 -7: RC Waveshapes Fig. 22 -6: Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

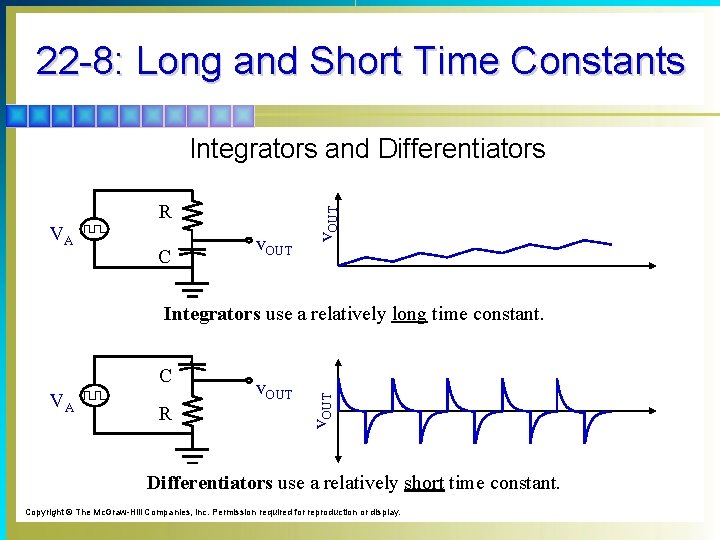
22 -8: Long and Short Time Constants § Useful waveshapes can be obtained by using RC circuits with the required time constant. § In practical applications, RC circuits are used more than RL circuits because almost any value of an RC constant can be obtained easily. § Whether an RC time constant is long or short depends on the pulse width of the applied voltage. § A long time constant can be arbitrarily defined as at least five times longer than the pulse width, in time. § A short time constant is defined as no more than onefifth the pulse width, in time.

22 -8: Long and Short Time Constants R VA C v. OUT Integrators and Differentiators C VA R v. OUT Integrators use a relatively long time constant. Differentiators use a relatively short time constant. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

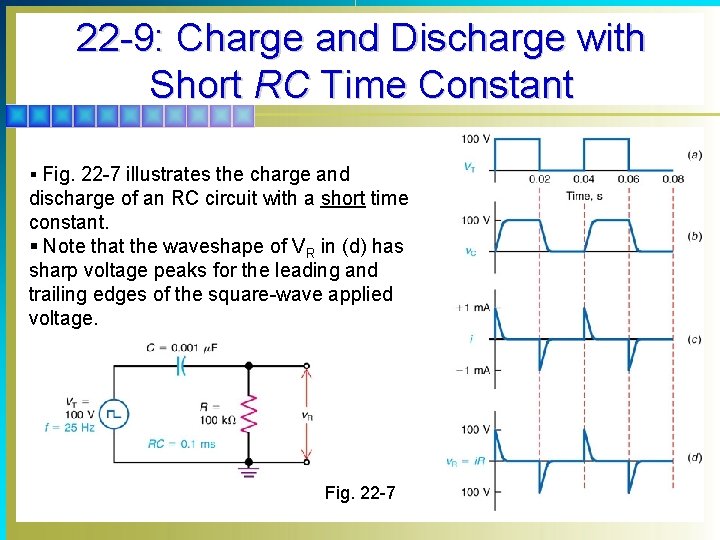
22 -9: Charge and Discharge with Short RC Time Constant § Fig. 22 -7 illustrates the charge and discharge of an RC circuit with a short time constant. § Note that the waveshape of VR in (d) has sharp voltage peaks for the leading and trailing edges of the square-wave applied voltage. Fig. 22 -7

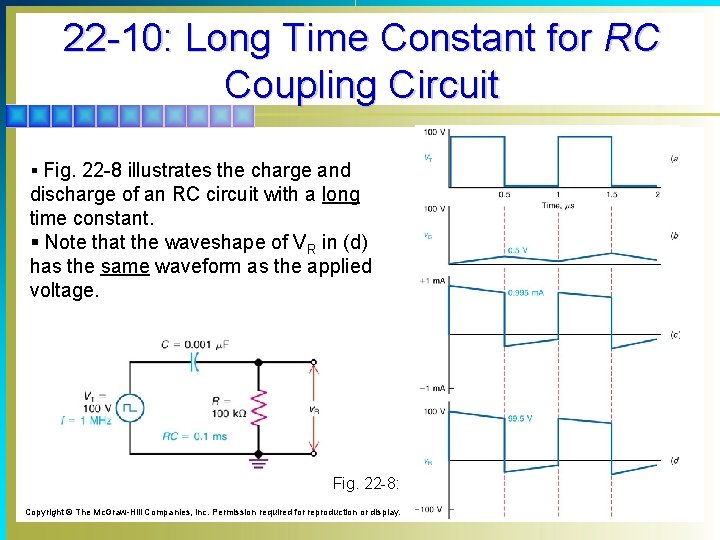
22 -10: Long Time Constant for RC Coupling Circuit § Fig. 22 -8 illustrates the charge and discharge of an RC circuit with a long time constant. § Note that the waveshape of VR in (d) has the same waveform as the applied voltage. Fig. 22 -8: Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

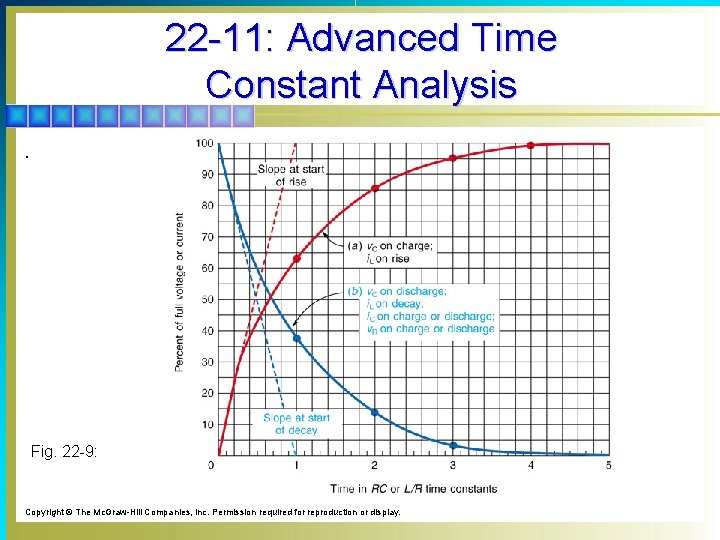
22 -11: Advanced Time Constant Analysis § Transient voltage and current values can be determined for any amount of time with a universal time-constant chart. § A universal time-constant chart is a graph of curves obtained by plotting time in RC or L/R time constants versus percent of full voltage or current. § An example of a universal time-constant chart for RC and RL circuits is shown in Fig. 22 -9 (next slide).

22 -11: Advanced Time Constant Analysis. Fig. 22 -9: Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

22 -12: Comparison of Reactance and Time Constant Table 22 -2 Comparison of Reactance XC and RC Time Constant Sine-Wave Voltage Nonsinusoidal Voltage Examples are 60 -Hz power line, af signal Examples are dc circuit turned on and voltage, rf signal voltage off, square waves, rectangular pulses Reactance XC = 1/(2πf. C) Time constant T = RC Larger C results in smaller reactance XC Larger C results in longer time constant Higher frequency results in smaller XC Shorter pulse width corresponds to longer time constant IC = VC/XC i. C = C(dv/dt) XC makes IC and VC 90° out of phase Waveshape changes between i. C and v. C