Chapter 22 Quantitative genetics Traits with a continuous

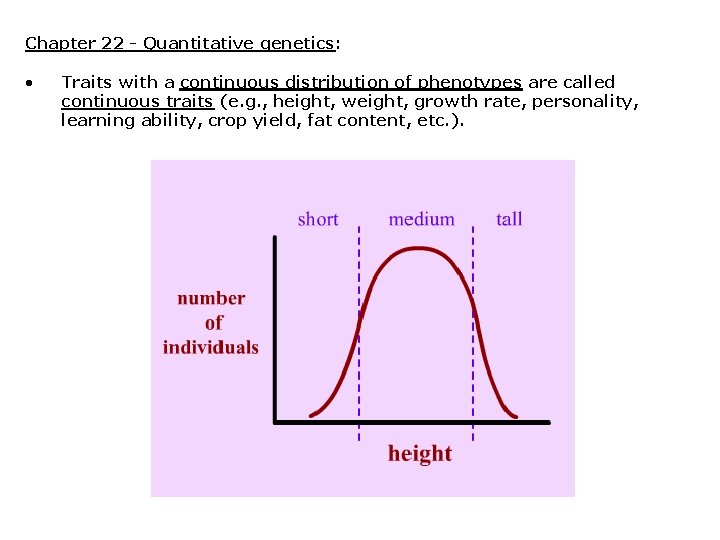
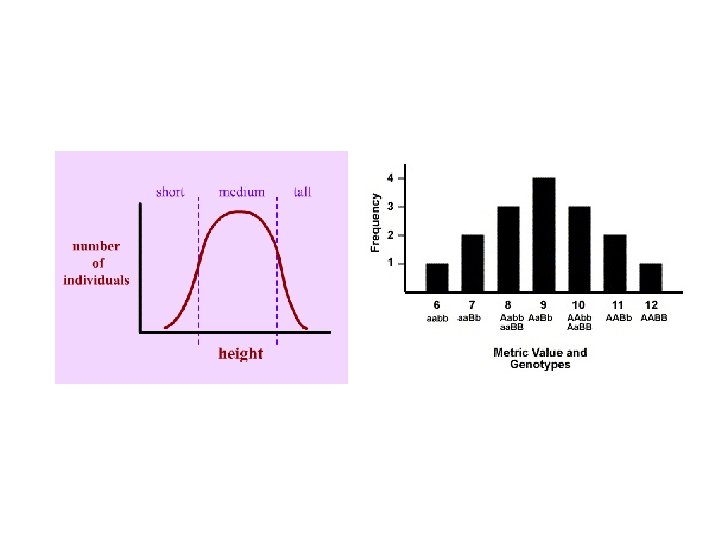
Chapter 22 - Quantitative genetics: • Traits with a continuous distribution of phenotypes are called continuous traits (e. g. , height, weight, growth rate, personality, learning ability, crop yield, fat content, etc. ).

Continuous traits arise from effects of: • Multiple loci (effects of many genes) • Pleiotropy (one gene has many effects) • Epistasis (gene interaction effects) • Variable expressivity and penetrance • Environment (produces a range of phenotypes)

Continuous traits: • Francis Galton and Karl Pearson (late 1800 s): Recognized that continuous traits are statistically correlated between parents and offspring, but could not determine how transmission occurs. • Wilhelm Johannsen (1903): Demonstrated that bean seed weight is partly heritable and partly environmental. • Sir Ronald Fisher (1890 -1962): First to demonstrate mathematically that Mendelian models of allele segregation apply to multiple genetic loci.

Types of questions studied in quantitative genetics: • How do genetics and the environment affect a trait? • Which and how many genes produce a set of phenotypes for a trait; where in the genome are they located? • Do some genes play a major role, whereas other genes modify or play a small role? • Do alleles interact to produce additive or epistatic effects? • How does selection affect the trait; does it affect other traits that may be linked? • If so what types of mating and selection produce desired phenotypes?

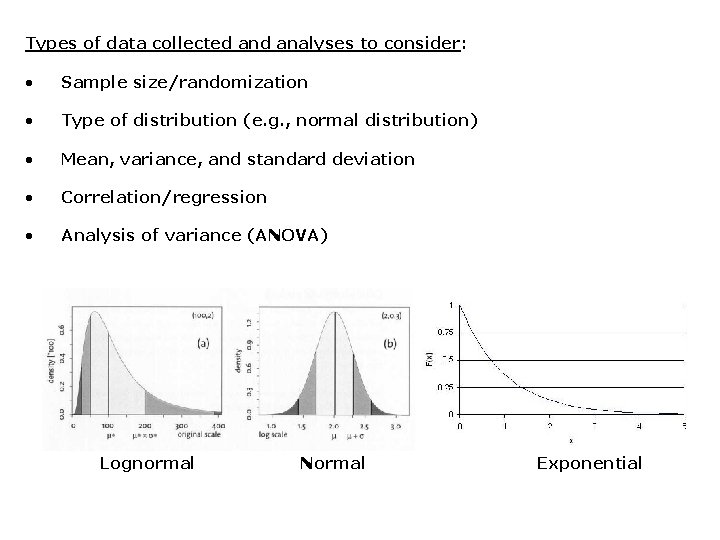
Types of data collected analyses to consider: • Sample size/randomization • Type of distribution (e. g. , normal distribution) • Mean, variance, and standard deviation • Correlation/regression • Analysis of variance (ANOVA) Lognormal Normal Exponential

Quantitative trait loci (QTLs): QTLs =specific genomic segments correlated with continuous phenotypic trait variation. Perform Genome Wide Association Study (GWAS) 1. Cross inbred lines with different phenotypes (homozygotes for different alleles at most loci) to produce heterozygotes. 2. Self F 1 or back cross to parental lines to increase phenotypic variation and segregation of traits. 3. Analyze F 2 with physical markers (microsatellites) that correlate with phenotypic variation. 4. Create a linkage map. 5. Calculate components of phenotypic variance (VP) due to genetic effects (VG) and components due to environment effects (VE). VP = VG + VE + 2 COVG, E + VG x E

Components of genetic variance: 1. Additive genetic variance (VA): effects of alleles at two or more loci contribute to phenotype. F 1 will appear intermediate to the parental phenotypes for repeated test crosses. 2. Dominance variance (VD): effects of alleles are not strictly additive; must consider how alleles interact in the heterozygote. F 1 will resemble one of the parental phenotypes. 3. Interaction variance (VI): accounts for epistatic interactions between two or more loci. F 1 phenotype is unpredictable. 1. VG = VA + V D + V I 2. VP = (VA + VD + VI) + VE + 2 COVG, E + VG x E

Calculate Lod Score (Logarithm of the Odds): 1. Lod = log of the ratio odds that two loci (or a locus and a trait) are linked with a recombination factor (q) greater than 0 and less than 0. 5. 2. z = log 10 {Prob(data|q)/Prob(data|0. 5)} 3. Lod score of +3. 00 (odds of 1000: 1) or greater is regarded as acceptable evidence for linkage. Lod 3 = 1000: 1 Lod 2 = 100: 1 Lod 1 = 10: 1

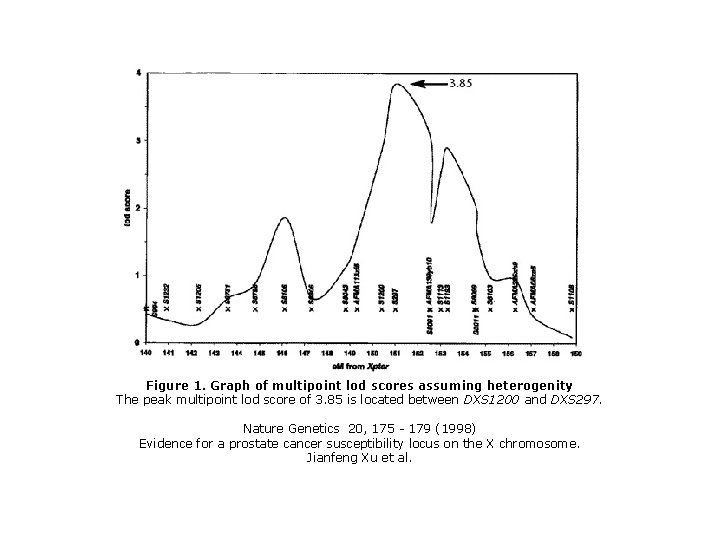
Figure 1. Graph of multipoint lod scores assuming heterogenity The peak multipoint lod score of 3. 85 is located between DXS 1200 and DXS 297. Nature Genetics 20, 175 - 179 (1998) Evidence for a prostate cancer susceptibility locus on the X chromosome. Jianfeng Xu et al.

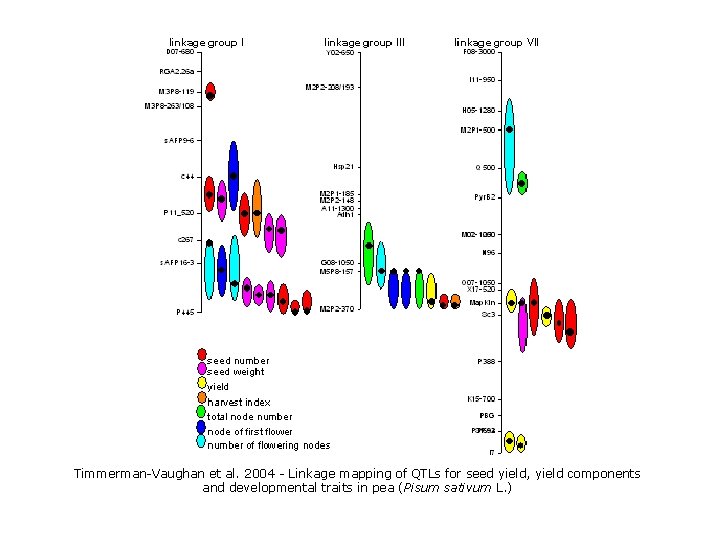
Timmerman-Vaughan et al. 2004 - Linkage mapping of QTLs for seed yield, yield components and developmental traits in pea (Pisum sativum L. )

Chromosome map of human QTLs for plasma concentrations of HDL-C, LDL-C and triglyceride levels. 2007. The Jackson Laboratory

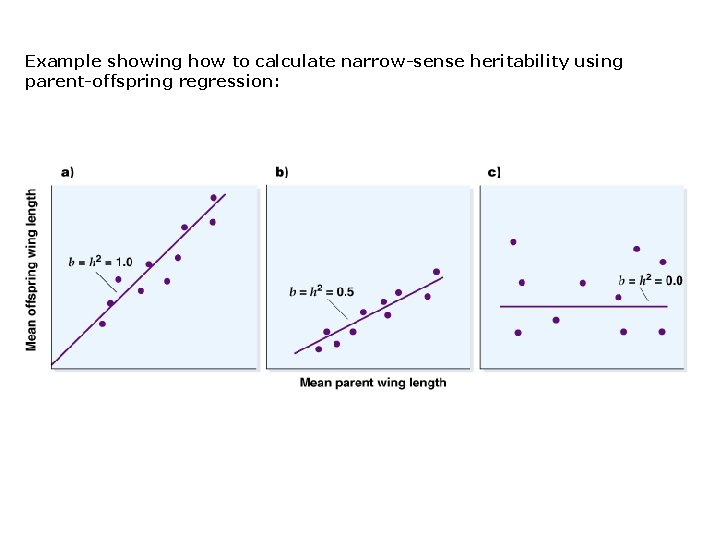
Broad- and Narrow-Sense Heritability: 1. Broad-sense heritability = h. B 2 = VG/VP 2. Narrow-sense heritability = h. N 2 = VA/VP 3. *Broad-sense heritability measures proportion of phenotypic variance among individuals in a population that results from genetic differences. 4. *Narrow-sense heritability measures proportion of phenotypic variance that results from additive genetic variance only. 5. *Narrow sense heritability is what can be used to predict resemblance between offspring and parents, between you and your parents. 6. *Heritability is a measure of variance and is only meaningful for characteristics of a population (not the individual).

Example showing how to calculate narrow-sense heritability using parent-offspring regression:

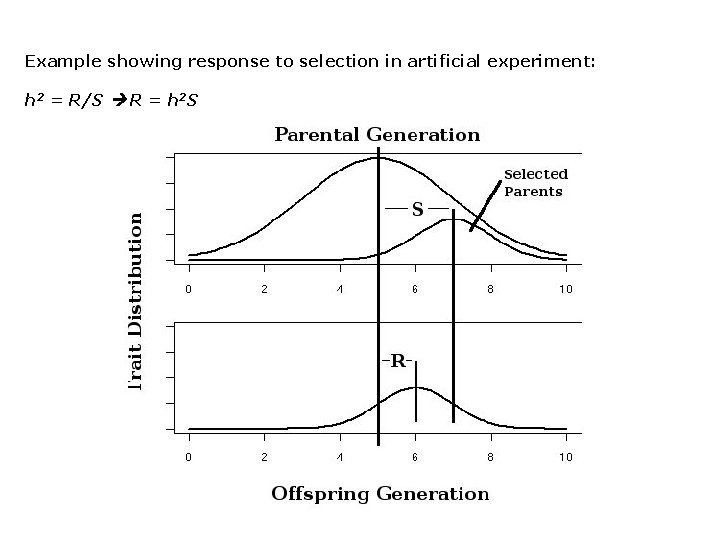
Example showing response to selection in artificial experiment: h 2 = R/S R = h 2 S

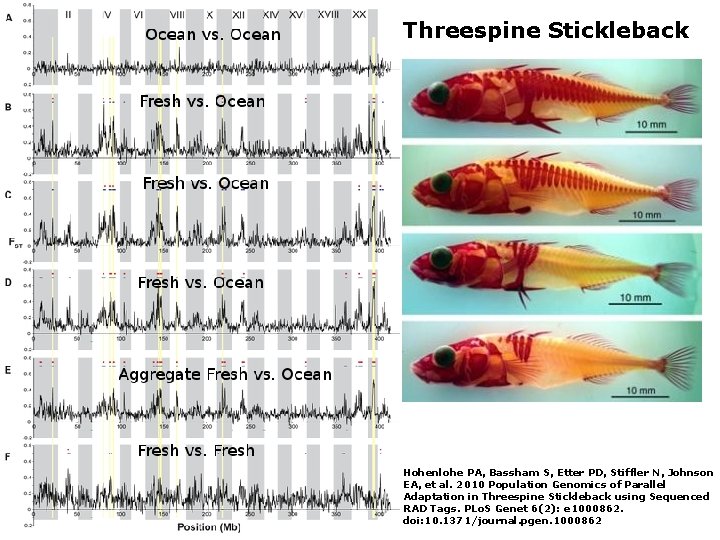
Genome Scan • Search for islands of genetic differentiation in otherwise undifferentiated genetic background. • Method of searching for genes for functionally important traits. • Does not require crossing experiment, but rather perform genomic scan (e. g. , next-generation sequencing) for two populations that differ in a single environmental variable subject to strong selection. • Works best for two populations that are in migration-selection balance equilibrium experiencing strong divergent selection and high gene flow. • Utilize measures such as Sewall Wright’s Fst • Examines linked patterns of statistically correlated divergence in different genes, which may result from correlated selection and/or divergence hitchhiking through depressed recombination.

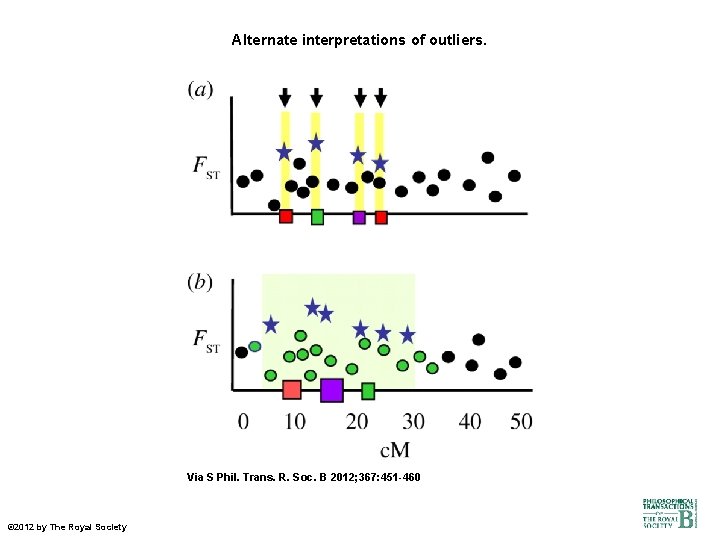
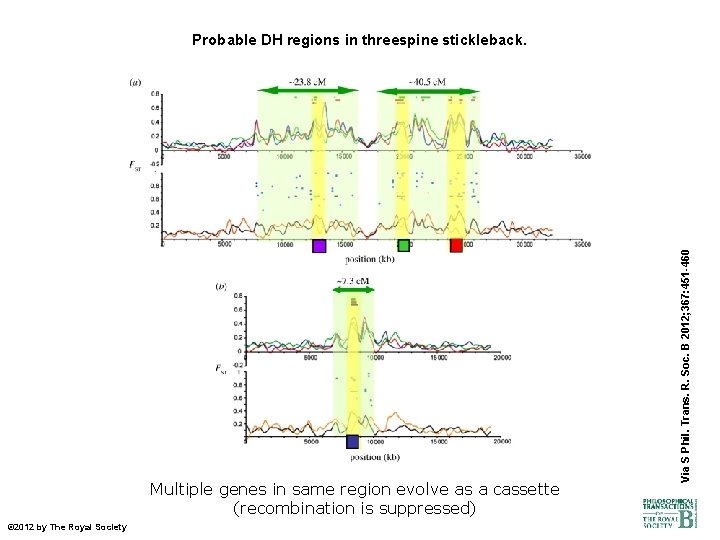
Alternate interpretations of outliers. Via S Phil. Trans. R. Soc. B 2012; 367: 451 -460 © 2012 by The Royal Society

Threespine Stickleback Hohenlohe PA, Bassham S, Etter PD, Stiffler N, Johnson EA, et al. 2010 Population Genomics of Parallel Adaptation in Threespine Stickleback using Sequenced RAD Tags. PLo. S Genet 6(2): e 1000862. doi: 10. 1371/journal. pgen. 1000862

Multiple genes in same region evolve as a cassette (recombination is suppressed) © 2012 by The Royal Society Via S Phil. Trans. R. Soc. B 2012; 367: 451 -460 Probable DH regions in threespine stickleback.