Chapter 22 Intermporalna efikasnost Intertemporal Efficiency 22 1

Chapter 22 Intermporalna efikasnost (Intertemporal Efficiency)

22. 1 Uvod • Vreme je suštinska komponenta ekonomske aktivnosti • Vreme stvara potrebu za analizom trade-off između sadašnjosti i budućnosti • Uključivanje vremena otvara nova pitanja za ekonomsku politiku koja se ne pojavljuju u statičkoj analizi • Primeri: sistem penzijskog osiguranja i uticaj ekonomske politika na privredni rast • Analiza ovih politika zahteva ekonomski model koji ima dinamičku/intertemporalnu strukturu 2

22. 1 Uvod • Konkurentski statički modeli (poglavlje 2) mogu da uključe vreme na sledeći način: – sve robe su datirane prema vremenu raspoloživosti – ugovori o budućoj trgovini su potpisani unapred – teoreme kojima se definišu uslovi efikasnosti tada važe • U ovom modelu svi potrošači su se dogovorili o budućoj trgovini, pre nego što je proizvodnja počela • Ravnoteža se uspostavlja kad se unapred odrede cene koje izjednačuju ponudu i tražnju za sve proizvode u svim budućim periodima • Ovakav način uključivanje vremena u ekonomske modele ne opisuje adekvatno stvarnost 3

22. 1 Uvod • Modeli preklapajućih generacija uključiji vreme u privredu na realniji način • U okvir u ovih modela se pretpostavlja da sa protokom vremena: – u privredu ulaze novi potrošači – stari potrošači napuštaju privredu – u svakom trenutku u privredi postoji skup mladih i starih potrošača, izmedju kojih postoji medjugeneracijska razmena/transferi proizvoda • Model realno opisuje životni ciklus, ali daje neke iznanadjujuće zaključke: konkurentska ravnoteža može da bude Pareto neefikasna, čak i ako nema ni jednog razlog za neuspeh tržišta (monopol i dr. ) • Postojanje Pareto neefikasnosti predstavlja mogući razlog za državnu intevenciju 4

22. 2 Model preklapajućih generacija • Protok vremena je povezan sa dve osobine privrede: • kapital može da se transferiše kroz vreme, ali se tokom vremena postepeno obezvredjuje • životni vek svakog pojedinca/potrošača je ograničan i relativno kratak u odnosu na privredu koja traje beskonačno • U modelima preklapajućih generacija vreme je podeljeno u diskretne periode – dužina perioda t je vremenski razmak između rodjenja jedna generacije i rodjenja naredne generacije • Ekonomska aktivnost se obavlja beskonačno • Na početku svakog perioda rađa se nova generacija mladih potrošača • Svaki potrošač živi u dva vremenska perioda • Broj stanovnika raste po konstantnoj stopi n • Ako generacija t ima Ht pripadnika tada je veličina generacije Ht+1 = [1 + n] Ht 5

22. 2 Model preklapajućih generacija • U svakom trenutku populacija se sastoji od dve uzastopne generacije - mladih i starih potrošača Generation t • Mladi i stari imaju različite motive za trgovinu jer se nalaze u različitim fazama životnog ciklusa Generation t+1 Generation t+2 Generation t+3 Time • Potrošači rade (zarađuju), troše i štede dok su mladi • U starosti žive od uštedjevine (glavnica+prinos) koju su ostvarili dok su bili mladi Figure 22. 1 Generational structure 6

22. 2 Model preklapajućih generacija • Privreda proizvodi samo jedan proizvod u svakom vremenskom periodu • Proizvodnja se ostvaruje upotrebom rada i kapitala • Proizvod se može potrošiti ili uštedeti • Štednjom se formira kapital koji se u narednom periodu upotrebljava kao input u proizvodnji • Potrošači planiraju potrošnju tako da maksimiziraju korisnost tokom životnog veka • Proizvodnja je odredjena tako da se maksimizira profit • Sva tržišta su konkurentska pa su cene za potrošače i proizvodjače date 7

22. 2 Model preklapajućih generacija • Stuktura životnog veka svakog potrošača je identična: – Svi rade samo dok su mladi i tada nude jednu jedinicu rada – ponuda je nelastična • Ukupna ponuda rada jednaka je broju mladih potrošača – U starosti niko ne radi, satri žive od štednje koju su akumlirali dok su radili • Dohodak zaradjen u mladosti se deli izmedju potrošnje i štednje • Potrošnja u starosti je jednaka štednji pls akmulisana kamata • Ljudi planiraju potrošnju tako da tokom života potroše sve što su zaradili – neto nasledje je nula • Svi potrošači su identični, razlikuju se samo po datumu rođenja 8

22. 2 Potrošači u modelu preklapajućih generacija • Potrošač rođen u periodu t maksimizira funkciju korisnosti (1) gde su i potrošnja u mladosti i starosti. • Budžetsko ograničenje u mladosti je: (2) gde je wt zarada za jedinicu rada, a štednja • Potrošnja u drugom periodu (starosti) je • (3) • Budžetsko ograničenja tokom životnog ciklusa je (4) • Maksimizacija funkcije korisnosti (5) Consumption when old Consumption when young Figure 22. 2 Consumer choice 9

22. 2 Proizvodnja u modelu preklapajućih generacija • Uprivredi postoji mnogo konkurentskih preduzeća i svako od njih proizvodi sa konstantnim prinosima • Agregatna proizvodnja se može opisati jednim reprezentativnim preduzećem • Zbog jednostavnosti zanemaruje se amortizacija kapitala, – – na kraju svakog perioda postoji kapital i proizvodnja u tom periodu kapital i proizvodnja mogu da se štede (reinvestiraju) ili potroše • Proizvodna funkcija je • Alokacije je izvodljiva ako je proizvodnja jednaka zbiru potrošnje dve generacije i štednje • (6) • Reprezantativno preduzeće bira rad i kapital tako da makimizira profit • (7) • Maksimizacija profita je postiže kada je • (8) (9) gde su Fk i Lk, granični proizvodi kapitala i rada, a rt i wt, kamatne stope i zarade 10

22. 2 Proizvodnja u modelu preklapajućih generacija • Odnos proizvodnje i rada je definisan sa yt = Yt/Lt • Dok je odnos kapitala i rada definisan sa kt = Kt/Lt • Proizvodna funkcija tada se može predstaviti kao funkcija od jednosg argumenta • (10) • Proizvodna‚ funkcija zadovoljava uslove: f(0)=0, • Tada su uslovi za maksimizaciju profita (11) (12) 11

22. 3 Ravnoteža u modelu preklapajućih generacija • U modelima preklapajućih generacija potreban uslov za ravnotežu je da potrošači maksimizuju korisnost, proizvođači profit da su tržišta svih proizvoda u ravnoteži • Na osnovu prethodnih uslova mogu se definisati dva koncepta ravnoteže – Intertemporalna ravnoteža pri kojoj je ponuda jednaka tražnji u svakom periodu – njom se odredjuje putanja endogenih varijabli koje se menjaju iz perioda u period • • – steady state ravnoteža u okviru koje su endogene varijable konstantne tokom vremena – dugoročno stanje privrede Ravnoteža na tržištu kapitala se uspostavlja kada je količina kapitala u periodu t+1 u proizvodnji jednaka štednji u periodu t (13) Deljenjam sa Ht (broj mladih) i korišćanjem identiteta i Ht=Lt, prethodna jednačina se može iskazati kao funkcija kt (14) 12

22. 3 Intertemporalna ravnoteža • Intertemporalna ravnoteža predstavlja niz varijabli koje dostižu ravnotežu u svakom periodu t • U svakom periodu endogenih – svi potrošači i maksimiraju korisnost ( jednačine 4 i 5) – reprezantativno preduzeće maksimira profit (jednačine 11 i 12) – tržište kapitala je u ravnoteži (jednačina 14) • Ravnoteža se uspostavlja preko sledećeg mehanizma • U periodu 1 postoji početni nivo kapitala po radniku k 1, ovaj kapital pripada staroj generaciji • Nivo kapitala i radne snage (mladi u periodu 1) odredjuje r 1 i w 1 na osnovu jednačina 11 i 12 • Istovremeno na osnovu jednačina 4, 5 i 14 određuje se nivo potrošnje mladih i starih u periodu 1, kao i nivo kapitala k 2 u periodu 2 • Ponavljenjem ovog procesa odredjuje se nivo endogenih varijabli u narednim periodima 13

22. 3 Dugoročna (steady state) ravnoteža • Steady state se može interpretirati kao dugoročna ravnoteža u privredi – sve varijable su konstantne • Stedy state jednačine kojima se odredjuju zarade i kamatne stope uz konstantan kapital po radniku (k) su: w = f(k) – kf’(k) i r = f’(k) • Svaki potrošač se suočava sa budžetskim ograničenjem • (15) gde je potrošnja u mladosti, a potrošnja u starosti • Ravnoteža na tržištu kapital je definisana uslovom • (16) • Napomena: prethodne jednačine su identične kao u dinamičkom modelu, samo što u steady state ne zavise od t 14

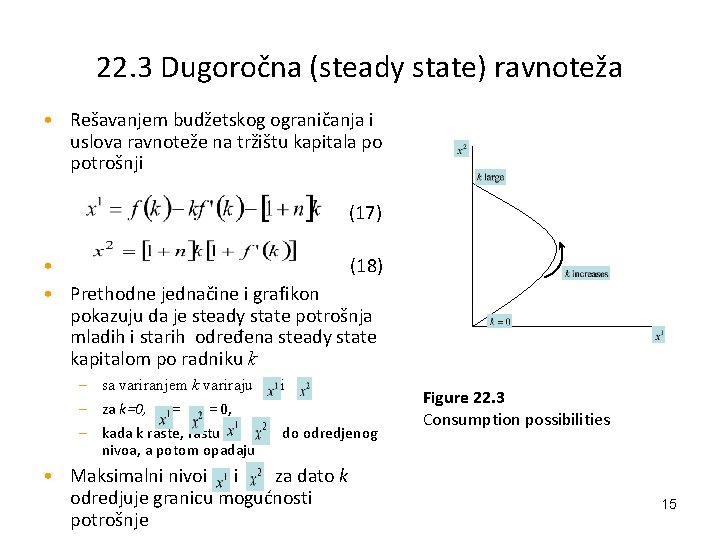
22. 3 Dugoročna (steady state) ravnoteža • Rešavanjem budžetskog ograničanja i uslova ravnoteže na tržištu kapitala po potrošnji (17) • (18) • Prethodne jednačine i grafikon pokazuju da je steady state potrošnja mladih i starih određena steady state kapitalom po radniku k – sa variranjem k variraju – za k=0, = = 0, – kada k raste, rastu i nivoa, a potom opadaju i do odredjenog • Maksimalni nivoi i za dato k odredjuje granicu mogućnosti potrošnje Figure 22. 3 Consumption possibilities 15

22. 3 Dugoročna (steady state) ravnoteža • Steady state ravnoteža je određena preferencijama potrošača i krivom potrošnih mogućnosti • Vrednost k odredjuje kamatnu stopu , koja definiše nagib budžetskog ograničenja • Steady state ravnoteža je u tački u kojoj najviša dostupna kriva infirentosti predstavlja tangentu budžetskog ograničenja, ravnoteža se uvek nalazi na krivoj potrošnih mogućnosti • Tačke a i b su na krivoj potrošnih mogućnosti ali ne predstavljaju steady-state ravnotežu Equilibrium a Gradient b Figure 22. 4 Steady-state equilibrium 16

22. 4 Optimalnost i efikasnost: zlatno pravilo • Sve tačke na krivoj potrošnih mogućnosti predstavljaju potencijalnu steady -state ravnotežu • Preferencije potrošača odredjuju steady state tačku na krivoj potrošnih mogućnosti i njoj odgovrajuće alokacije potrošnje i odnos kapitala po radniku • U steady state svi potrošači u svim generacijama imaju isti plan potrošnje tokom životnog ciklusa, pa su pitanja raspodele dohotka ireleventna • Odnos kapitala i rada koji maksimizira potrošnju u svim periodima predstavlja zlatno pravilo o odnosu kapitala i rada • Da li konkuretska ravnoteža zadovoljava zlatno pravilo? 17

22. 4 Optimalnost i efikasnost: zlatno pravilo • Pri izvodjenju zlatnog pravila polazi se od toga da je potrošnja u svim periodima jednaka poizvodnji umanjenoj za prirast kapitala (=štednja) (19) • U stedy state prethodni izraz odredjuje potrošnju u odnosu na dati kapital po radniku (20) • Zlatno pravilo za potrošnju u prvom periodu x 1 i kapital k dobija se maksimizacijom uz ograničenje (20) 18

22. 4 Optimalnost i efikasnost: zlatno pravilo • Potreban uslov prvog reda za x 1 je: U 1 –(1+n)U 2=0 iz čega sledi da je zlatno pravilo za graničnu stopu supstitucije potrošnje izmedju prvog i drugog perioda dato sa (1+n) • Uslog prvog reda za k je: U 2(1+n)(f(k)-n)=0, iz čega sledi da optimalni nivo k zadovoljava f’(k*) = n, gde je k* zlatno pravilo za odnos kapitala i rada • U konkurentkoj ekonomiji maksimizacija profita se postiže pri f’(k) = r, • Konkurentska ekonomije dostiže steady state ravnotežu sa r=n, odnosno u konkurentskoj ekonomiji zlatno pravilo se dostiže kada je kamatna stopa jednaka stopi rasta poulacije – tada je k=k* 19

22. 4 Optimalnost i efikasnost • Steady state ravnoteža postoji kada važi f’(k) = r • Konkurentska ravnoteža zadovoljava zlatno pravilo ako važi r = n i tada se maksimizuje potrošnju po stanovniku • Ako r ≠ n tada konkurentska ravnoteža na maksimizuje potrošnju po stanovniku • Konkurentska ravnoteža može da bude Pareto neefikasna • Neefiskanost može da postoji ako nema tršižnih poremećaja (monopol, ekterni efekt, javna dobra, asimetrične informacije) 20

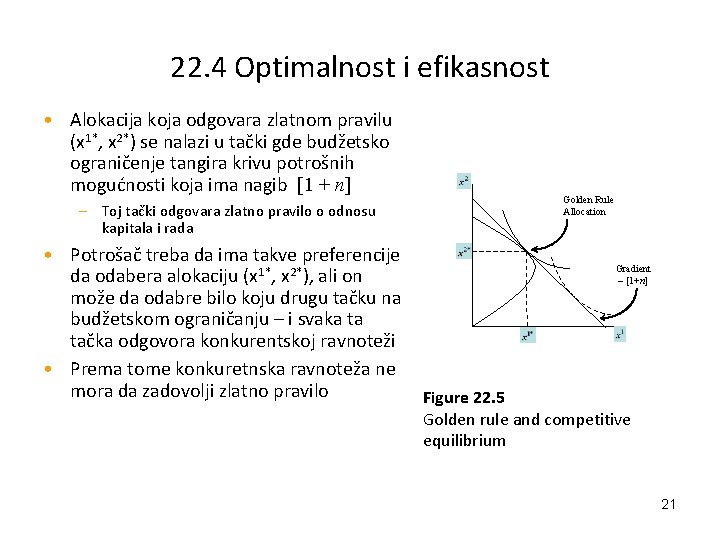
22. 4 Optimalnost i efikasnost • Alokacija koja odgovara zlatnom pravilu (x 1*, x 2*) se nalazi u tački gde budžetsko ograničenje tangira krivu potrošnih mogućnosti koja ima nagib [1 + n] – Toj tački odgovara zlatno pravilo o odnosu kapitala i rada • Potrošač treba da ima takve preferencije da odabera alokaciju (x 1*, x 2*), ali on može da odabre bilo koju drugu tačku na budžetskom ograničanju – i svaka ta tačka odgovora konkurentskoj ravnoteži • Prema tome konkuretnska ravnoteža ne mora da zadovolji zlatno pravilo Golden Rule Allocation Gradient – [1+n] Figure 22. 5 Golden rule and competitive equilibrium 21

22. 4 Optimalnost i efikasnost • Ako je k > k* (tada je r < n) pa je ekonomija prekapitlizovana – previše je investirano u prošlosti • Investicije su bila toliko visoke da nisu bile opravdane sa stanovništa dugoročne maksimizacije potrošnje • U tom slučaju postoji mogućnost Pareto poboljšanja : – potrošači u tekućem periodu mogu da potroše do kapitala zbog čega ća se povećati njihovo blagostanje – smanjeni stok kapitala približiće privredu zlatnom pravilu k* čime će se maksimizovati blagostanje svih budućih generacija • Stoga, kada je k > k* steady state konkurentska ravnoteža je Pareto neefikasna • Ekonomija je tada dinamički neefikasna – investicije kao %BDP je opravdano povećavati samo do određenog nivoa 22

22. 4 Optimalnost i efikasnost • Ako je k < k* (pa je r > n) tada je ekonomija potkapitalizovana – investicije su u prošlosti bile nedovoljne • Tada nije moguća da se ostvari Pareto pobovljšanje: – neophodno je da se kapital poveća da bi se približio zlatnom pravilu – da bi se to dogodilo potrošači u sadašnjem periodu moraju da smanje potrošnju (zbog toga se smanjuje njihovo blagostanje) kako bi povećali k i približili se zlatnom pravilu k* – potrošnja svih budućih generacija se povećava jer raste k • Stoga kada je k ≤ k* konkurentska ravnoteža je Pareto efikasna • Tada je ekonomija dinamički efikasna 23

22. 4 Optimalnost i efikasnost • Ne postoji jednostavno i ubedljivo objašnjenje Pareto neefikasnosti u modelima preklapajućih generacija • Neka standardna objašnjenja neefikasnosti koja se koriste u ekonomskoj teoriji moraju se odbaciti: – po pretpostavci ne postoje nesavršensti tržišta (monopoli i dr. ), pa cene, uključujući i kamatne stope šalju adekvatne signale • Ipak, postoje određeni formalni razlozi koji generišu neefikasnst: – u modelu preklapajućih generacija privreda funkciniše beskonačno – u beskonačnom periodu postoji beskonačan broj potrošača – proizvodi u različitim periodima se mogu posmatrati kao različiti proizvodi, pa privreda ima beskonačan broj proizvoda • Nefiksnost se javlja samo kada postoji beskonačno mnogo potrošača i priozvoda (dupla beskonačnost) – ako ima beskonačno potrošača, a konačno proizvoda privreda odgovara uslovima savršene konkurencije – ako postoji beskonačno proizvoda i konačan broj potrošača privred je efikasna 24

22. 5 Testiranje efikasnosti • Zlatno pravilo i dinamička efikasnost se mogu testirati poređenjem r i n • Privreda je: – dinamički efikasna ako je r ≥ n – dinamički neefikasna ako je r < n • Uslov za poredjenje je da n bude konstantno – u stvarnosti to nije slučaj, n može da bude i negativno • Opštiji test: u steady state stopa rasta kapitala je jednaka stopi rast populacije • Opštiji test dinimičke efikasnosti se zasniva na poređenju: – investicije u svakom peridu su n. K – plaćanja vlasnicima kapitala (dividende) u svakom periodu su r. K • Ekonomija su dinamički efikasna ako je r. K - n. K≥ 0, što je zadovoljeno ako je r≥n • Ako važi prethodne nejednakost bruto profit (profit+ amortizacija) je dovoljan za finansiranje bruto investicija (amortizacijy +nove investicije), a može (a ne mora) da postoji i višak koji troše potrošači 25

22. 5 Testiranje efikasnosti • U tabeli 22. 1 je prikazana razlika bruto profita i bruto investicija za nekoliko zemalja • Sve razlike su pozitivne, što znači da su sve privrede dinamički efikasne • Da bi važilo zlatno pravilo uslov je da r. K – n. K= 0 – sve privrede u Tabeli znatnije odstupaju od zlatnog pravila Table 22. 1 Gross profit minus investment as a proportion of GDP 26

22. 6 Zaključci • Modeli preklapajućih generacija opisuju razvoj privrede tokom vremena • Oni se zasnivaju na: – činjenici - da je život svakog potrošača izrazito kratak u odnosu na period u kome postoji privreda, – pretpostavci – da svaki potrošač alocira potrošnju tokom životnog ciklusa na racionalan način • Zlatno pravilo opisuje optimalnu dinamiku kapitala koja maksimizuje potrošnju po stanovniku • Konkurentska ravnoteža u privredi može da bude Pareto neefikasna zbog preterane akumulacije kapitala – pretpostavljeni beskonačan broj potrošača i proizvoda je uzrok nefiksanosti konkurentne privrede • Efikasnost se testira poređenjem stope rasta populacije i kamatne stope ili bruto profita i investicija 27

Reading • Essential reading – Hindriks, J and G. D. Myles (2013) Intermediate Public Economics. (Cambridge: MIT Press) Chapter 22. • Further reading – Abel, A. B. , Mankiw, N. G. , Summers, L. H. and Zeckhauser, R. J. (1989) ‘Assessing dynamic efficiency’, Review of Economic Studies, 56, 1 - 19. – Diamond, P. A. (1965) ‘National debt in a neo-classical growth model’, Journal of Political Economy, 55, 1126 - 1150. – Samuelson, P. A. (1958) ‘An exact consumption-loan model of interest with or without the social contrivance of money’, Journal of Political Economy, 66, 467 - 482. – Diamond, P. A. (1965) ‘National debt in a neo-classical growth model’, Journal of Political Economy, 55, 1126 - 1150. 28

Reading • Challenging reading – Geanakoplos, J. (1987) ‘Overlapping generations model of general equilibrium’, in J. Eatwell, M. Milgate and P. Newman (eds. ) The New Palgrave: A Dictionary of Economics (London: Macmillan). – Hahn, F. H. (1982) Money and inflation (Oxford: Basil Blackwell). – Shell, K. (1971) ‘Notes on the economics of infinity’, Journal of Political Economy, 79, 1002 - 1011. 29