Chapter 21 The Kinetic Theory of Gases Ideal

Chapter 21 The Kinetic Theory of Gases

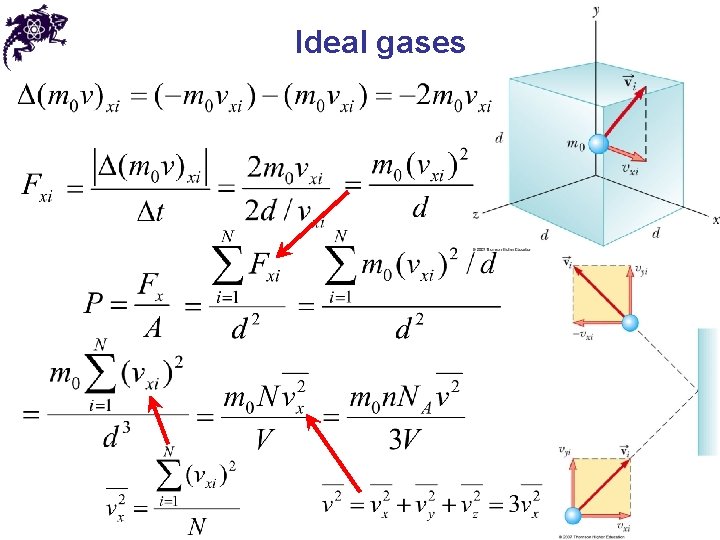
Ideal gases • The gas under consideration is a pure substance • All molecules are identical • Macroscopic properties of a gas: P, V, T • The number of molecules in the gas is large, and the average separation between the molecules is large compared with their dimensions – the molecules occupy a negligible volume within the container • The molecules obey Newton’s laws of motion, but as a whole they move randomly (any molecule can move in any direction with any speed)

Ideal gases • The molecules interact only by short-range forces during elastic collisions • The molecules make elastic collisions with the walls and these collisions lead to the macroscopic pressure on the walls of the container • At low pressures the behavior of molecular gases approximate that of ideal gases quite well

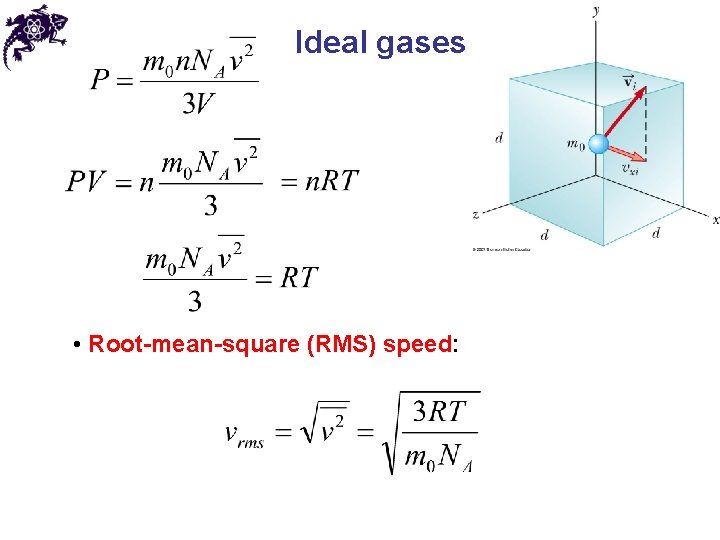
Ideal gases

Ideal gases • Root-mean-square (RMS) speed:

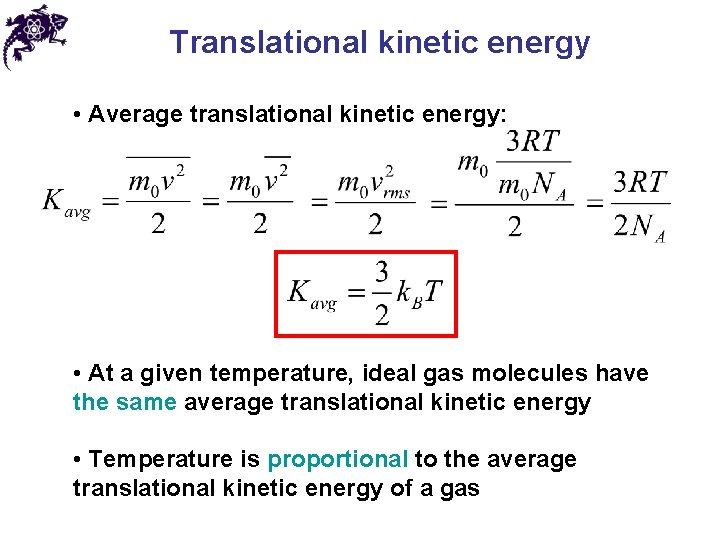
Translational kinetic energy • Average translational kinetic energy: • At a given temperature, ideal gas molecules have the same average translational kinetic energy • Temperature is proportional to the average translational kinetic energy of a gas

Internal energy • For the sample of n moles, the internal energy: • Internal energy of an ideal gas is a function of gas temperature only

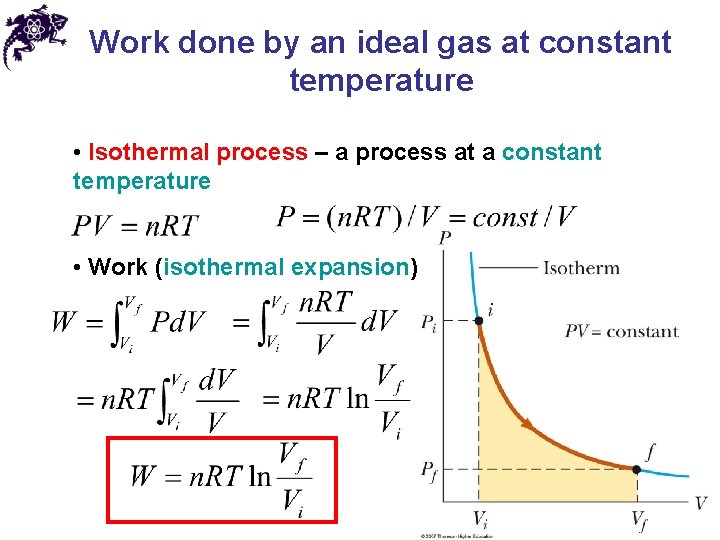
Work done by an ideal gas at constant temperature • Isothermal process – a process at a constant temperature • Work (isothermal expansion)

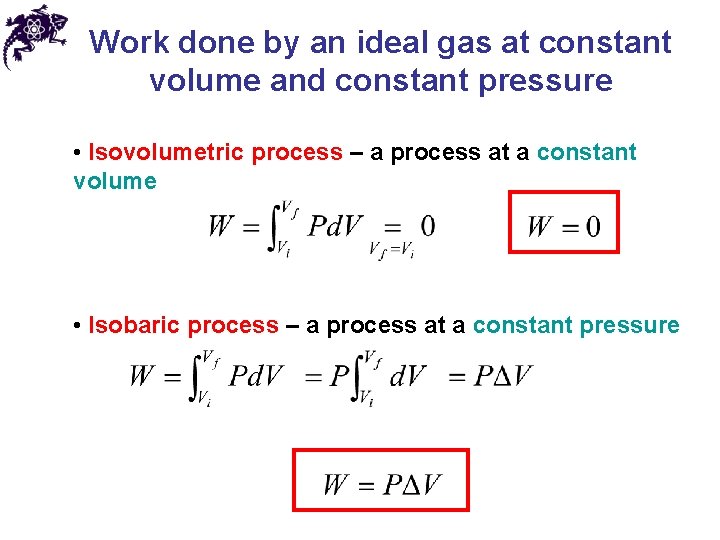
Work done by an ideal gas at constant volume and constant pressure • Isovolumetric process – a process at a constant volume • Isobaric process – a process at a constant pressure

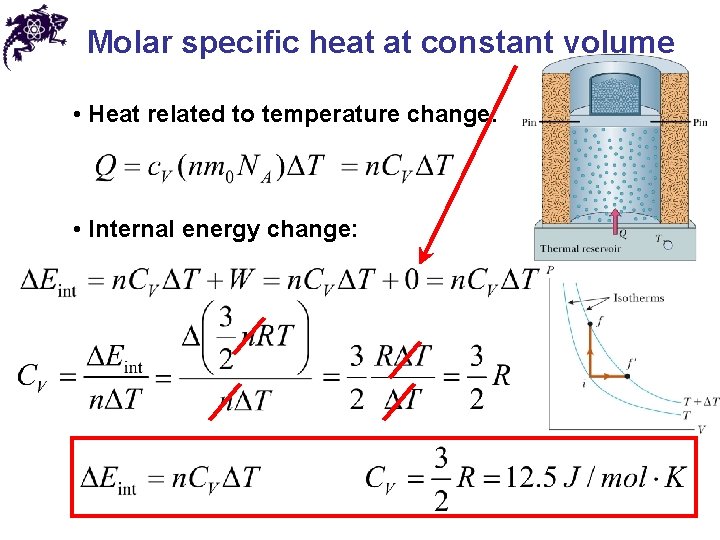
Molar specific heat at constant volume • Heat related to temperature change: • Internal energy change:

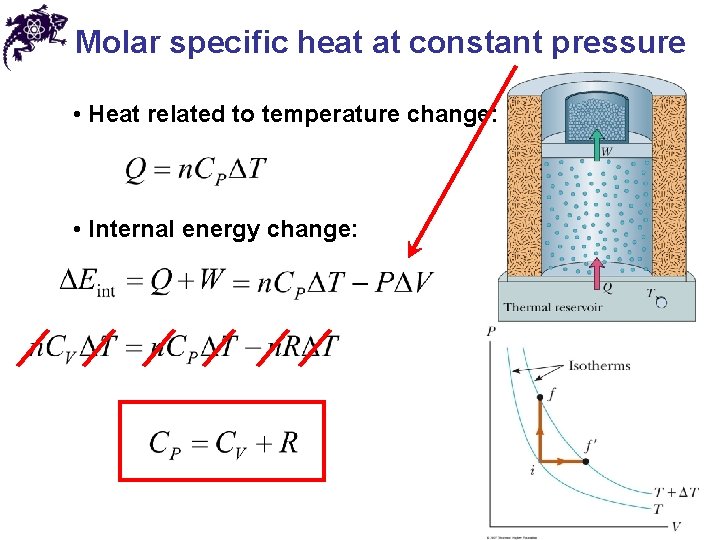
Molar specific heat at constant pressure • Heat related to temperature change: • Internal energy change:

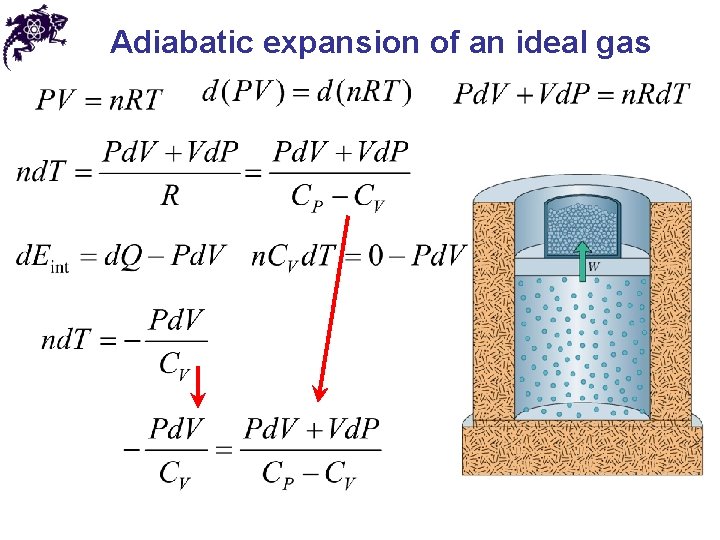
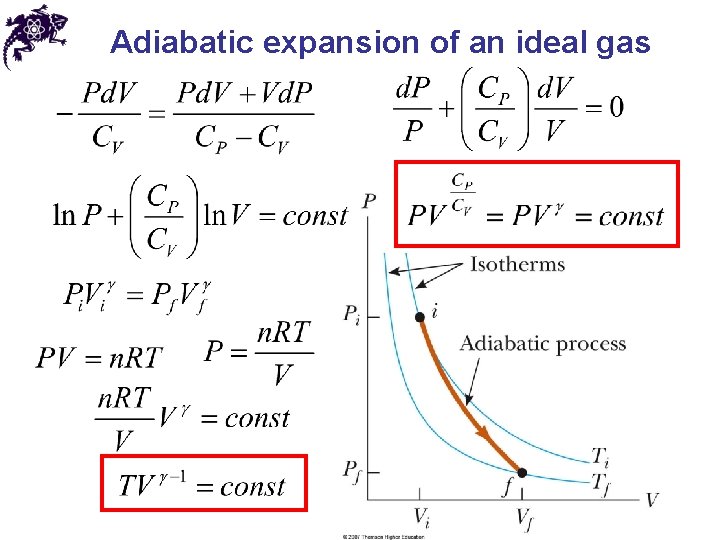
Adiabatic expansion of an ideal gas

Adiabatic expansion of an ideal gas

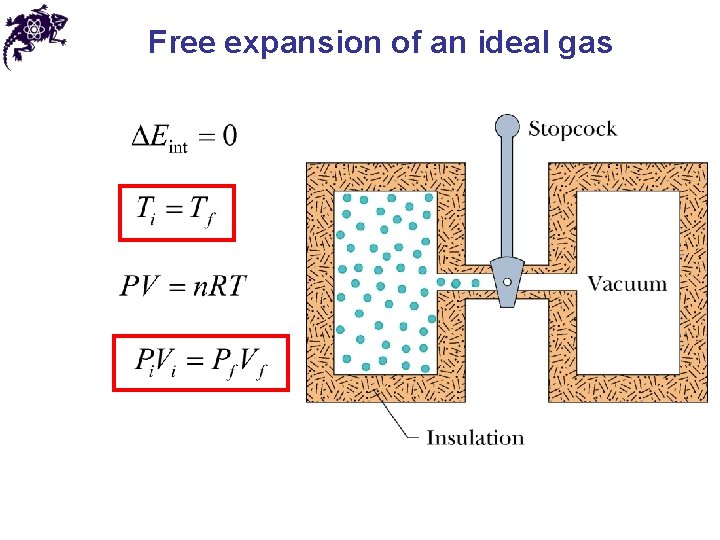
Free expansion of an ideal gas

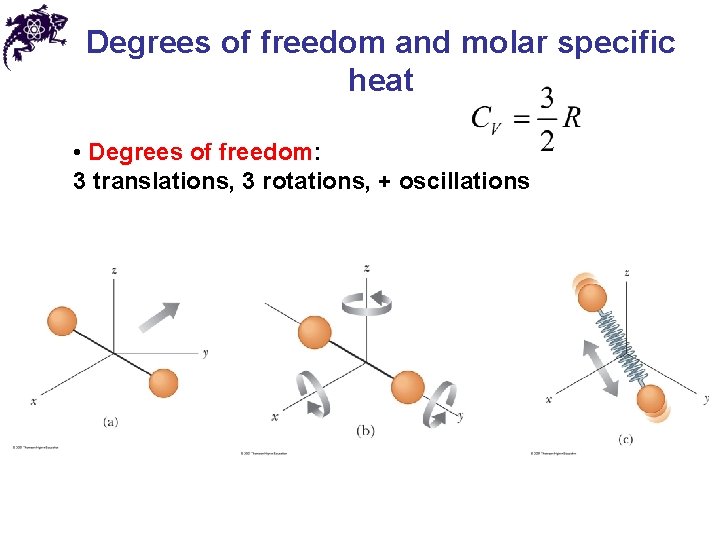
Degrees of freedom and molar specific heat • Degrees of freedom: 3 translations, 3 rotations, + oscillations

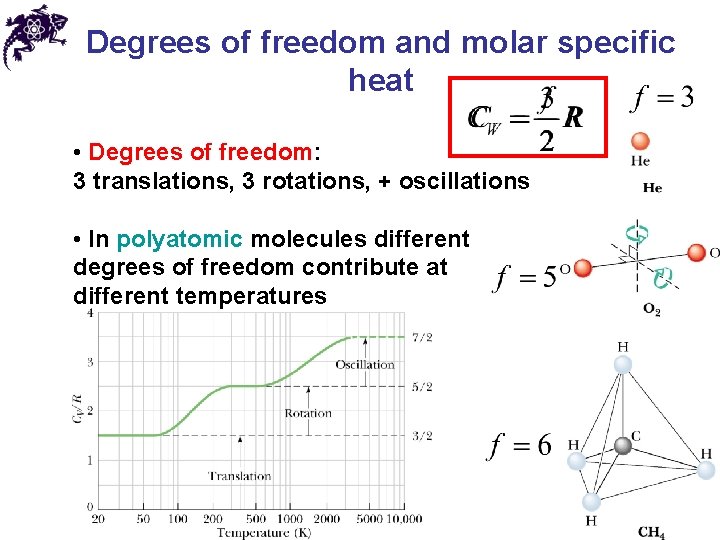
Degrees of freedom and molar specific heat • Degrees of freedom: 3 translations, 3 rotations, + oscillations • In polyatomic molecules different degrees of freedom contribute at different temperatures

Chapter 21 Problem 13 A 1. 00 -mol sample of hydrogen gas is heated at constant pressure from 300 K to 420 K. Calculate (a) the energy transferred to the gas by heat, (b) the increase in its internal energy, and (c) the work done on the gas.

Chapter 21 Problem 27 Consider 2. 00 mol of an ideal diatomic gas. (a) Find the total heat capacity at constant volume and the total heat capacity at constant pressure, assuming the molecules rotate but do not vibrate (b) Repeat part (a), assuming the molecules both rotate and vibrate.

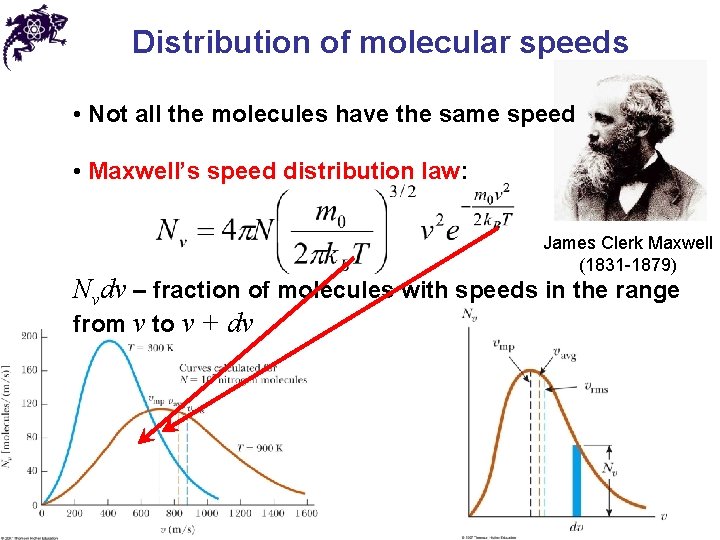
Distribution of molecular speeds • Not all the molecules have the same speed • Maxwell’s speed distribution law: James Clerk Maxwell (1831 -1879) Nvdv – fraction of molecules with speeds in the range from v to v + dv

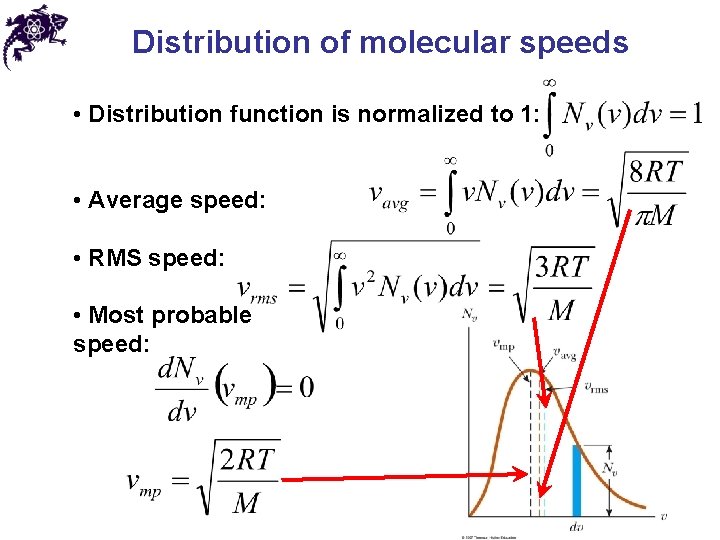
Distribution of molecular speeds • Distribution function is normalized to 1: • Average speed: • RMS speed: • Most probable speed:

Chapter 21 Problem 44 As a 1. 00 -mol sample of a monatomic ideal gas expands adiabatically, the work done on it is – 2500 J. The initial temperature and pressure of the gas are 500 K and 3. 60 atm. Calculate (a) the final temperature and (b) the final pressure.

Questions?

Answers to the even-numbered problems Chapter 21 Problem 8 (a) 2. 28 k. J (b) 6. 21 × 10− 21 J

Answers to the even-numbered problems Chapter 21 Problem 12 (a) 209 J (b) 0 (c) 317 K

Answers to the even-numbered problems Chapter 21 Problem 14 (a) 118 k. J (b) 6. 03 × 103 kg

Answers to the even-numbered problems Chapter 21 Problem 42 (a) 3. 65 v (b) 3. 99 v (c) 3. 00 v (d) 106 m 0 v 2/V (e) 7. 98 m 0 v 2