CHAPTER 20 CAPITAL EXPENDITURE DECISIONS 1 Chapter Overview

CHAPTER 20 CAPITAL EXPENDITURE DECISIONS 1

Chapter Overview q What is a capital expenditure, and what are the four steps in a capital expenditure decision? q What does a company include in the initial cost of a capital expenditure proposal? q What are the relevant costs of a capital expenditure proposal, and how do operating income, depreciation, and ending cash flows affect these costs? q How does a company determine the rate of return it requires on a capital expenditure proposal? 2

Chapter Overview q How does a company use the net present value method to evaluate a capital expenditure proposal? q What is the difference between the payback method and the average rate of return on investment method for evaluating a capital expenditure proposal? q How does a company decide which capital expenditure proposal to accept when it has several proposals that accomplish the same thing, or when it cannot obtain sufficient cash to make all of its desired investments? 3

Capital Expenditure Decisions q A capital expenditure decision is a long-term decision in which a company determines whether or not to make an investment (cash payment) at the time of the decision in order to obtain future net cash receipts totaling more than the investment. q The future net cash receipts related to the investment provide a “return” on the investment, which is the reason the company wants to make the expenditure in the first place. 4

Capital Expenditure Decision Process q Estimate the initial cash payments required. q Estimate the future cash receipts and payments (cash flows) expected. q Determine the company’s cost of providing the cash to make the investment. q Determine whether the estimated future cash flows will provide a return sufficient (based on the time value of money) to cover the cost of providing the cash for the investment. 5

Estimating the Initial Cash Payment q The initial cost of a capital expenditure is the expected cash payment to be made to put the proposal into operation. q For example, if a company is deciding whether or not to invest in a new machine that it will use for six years, the initial cash payment equals the cost of acquiring the machine including transportation and set up costs: 6

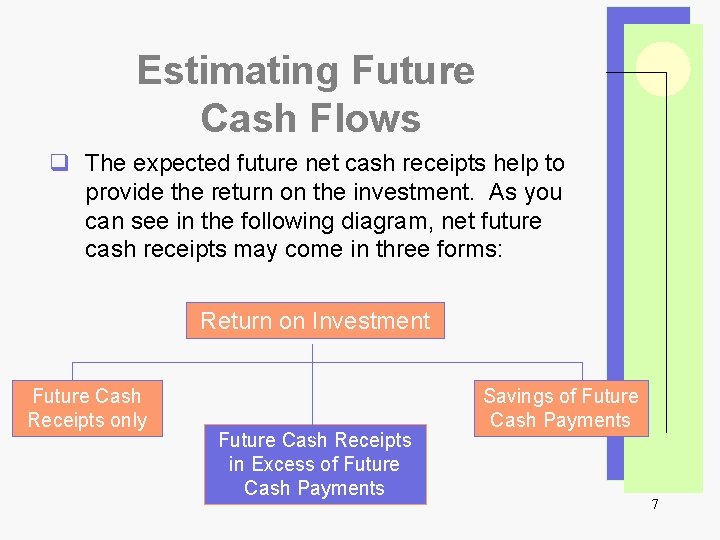
Estimating Future Cash Flows q The expected future net cash receipts help to provide the return on the investment. As you can see in the following diagram, net future cash receipts may come in three forms: Return on Investment Future Cash Receipts only Future Cash Receipts in Excess of Future Cash Payments Savings of Future Cash Payments 7

Estimating Relevant Cash Flows q When estimating future cash flows, it is important to identify the expected relevant cash flows and to estimate the number of years over which these cash flows will occur. q Relevant cash flows are future cash flows that differ, either in amount or in time, as a result of accepting a capital expenditure proposal. q To be relevant, a cash flow must (1) occur in the future, (2) result from activities required by the proposal, and (3) cause a change in the company’s existing cash flows. 8

Operating Income and Annual Cash Flows q When a company estimates its relevant future cash flows from a capital expenditure proposal, it uses the best available information from its predictions. q Frequently, the best available information is its expected future additional operating revenues and expenses. q Since revenues and expenses are usually indications of future cash inflows and outflows, this is a reasonable approach to take. 9

Treatment of Depreciation q Depreciation is an expense for which there is no future cash outflow. q If Unlimited Decadence plans to purchase a machine for $1, 000 cash and use the machine for 10 years when the estimated residual value is $100, the yearly straight-line depreciation expense for each of the 10 years will be $90 ($1, 000 - $100/10). q Since it plans to pay cash for the machine on the date of purchase, the company would make no cash payments for the machine during any of the 10 years it is used, even though depreciation is recorded. 10

Ending Cash Flows q A capital expenditure proposal may have some relevant cash flows occurring at the end of the project’s life. q For example, if there is an expected residual value at the end of the useful life of property, plant, or equipment, this represents a future cash receipt. In effect, the residual value is what can be obtained if the asset is disposed of at that time. q Likewise, the receipts from investing in additional working capital (i. e. , inventory) is recovered when the inventory is ultimately sold. 11

Required Return on Investment q For any capital expenditure proposal, a question arises as to the company’s required return on its investment. q The required return is equal to the cost of providing cash for the investment and is expressed as a percentage rate. For example, a 15% return means that the cost is 15 cents for every dollar invested. q A company’s financial position only improves if the proposal provide a return greater that the cost of providing the cash for the investment (i. e. , in other words, greater than 15% in this example. ) 12

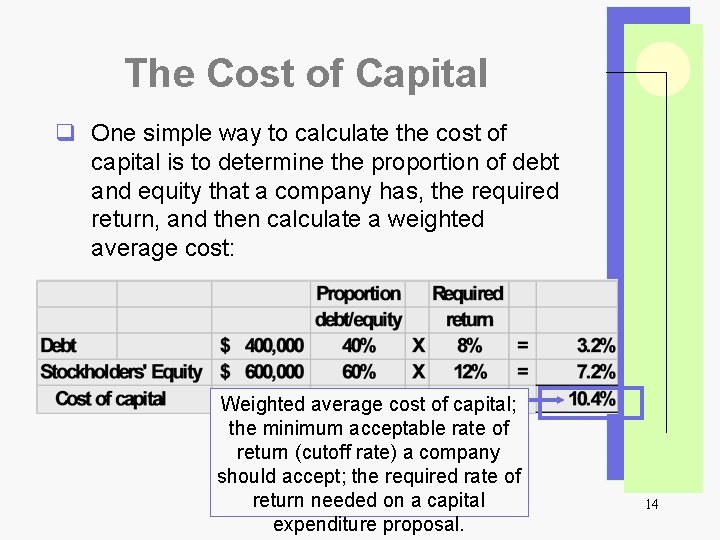
The Cost of Capital q The rate that measures the cost to a company of providing cash for investments is called the company’s cost of capital. q The cost of capital is the weighted-average cost (rate of return) it must pay to all sources of capital (investors and creditors). q It is calculated by the weighted-average of a firm’s debt and equity financing. 13

The Cost of Capital q One simple way to calculate the cost of capital is to determine the proportion of debt and equity that a company has, the required return, and then calculate a weighted average cost: Weighted average cost of capital; the minimum acceptable rate of return (cutoff rate) a company should accept; the required rate of return needed on a capital expenditure proposal. 14

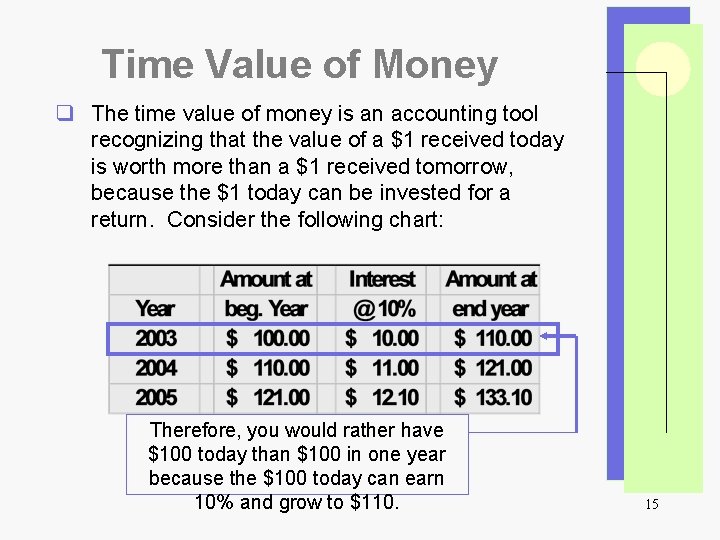
Time Value of Money q The time value of money is an accounting tool recognizing that the value of a $1 received today is worth more than a $1 received tomorrow, because the $1 today can be invested for a return. Consider the following chart: Therefore, you would rather have $100 today than $100 in one year because the $100 today can earn 10% and grow to $110. 15

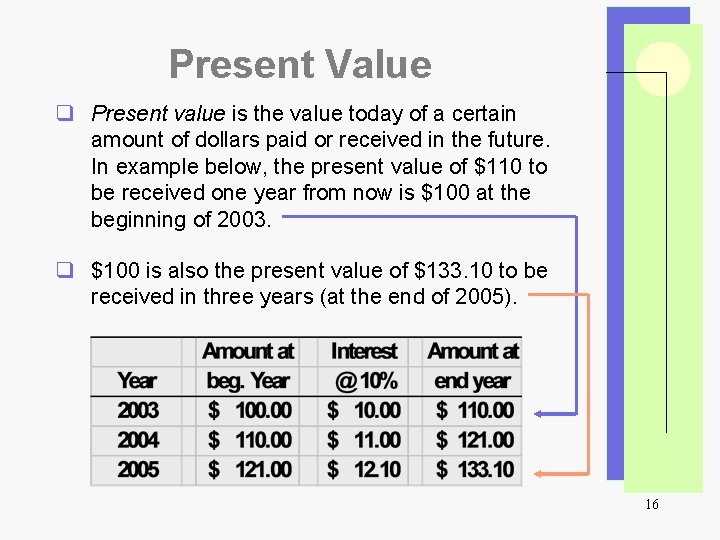
Present Value q Present value is the value today of a certain amount of dollars paid or received in the future. In example below, the present value of $110 to be received one year from now is $100 at the beginning of 2003. q $100 is also the present value of $133. 10 to be received in three years (at the end of 2005). 16

Compound Interest q Compound interest is interest that accrues on both the principal and the past (unpaid) interest. Thus, during 2003, interest of 10% accrues on the principal of $100, making a total of $110 at the end of 2003. q In 2004, interest of 10% accrues on the $110 (the principal and the 2003 interest), which yields principal and interest at the end of 2004 of $121. 00 and so on. Compounding principles illustrates the concept that time is money and is the basis for time value of money 17 computations.

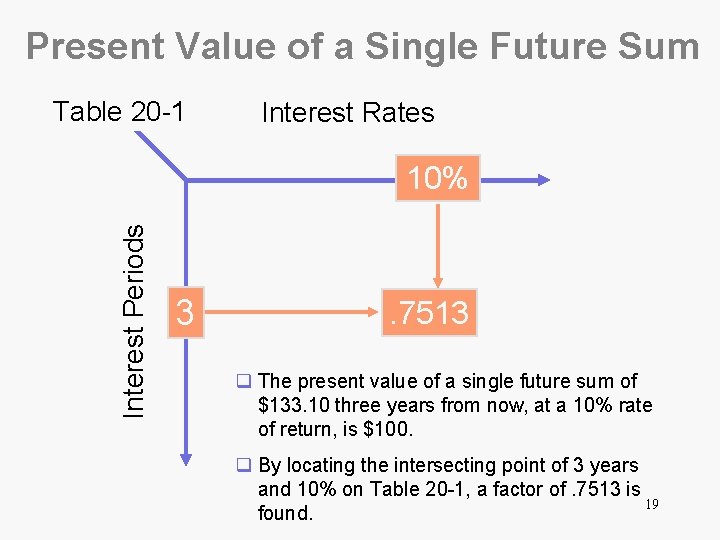
Present Value of a Single Future Sum q Present value of a single future sum was illustrated in our previous example. The present value of $110 (a future sum) today is $100. q A single future amount is a onetime future cash flow. For example, if Unlimited Decadence plans to use a mixing machine for three years and then sell it, the cash it will receive from the sale in three years in a single future sum. q Present value tables can be used to calculate these amounts. 18

Present Value of a Single Future Sum Table 20 -1 Interest Rates Interest Periods 10% 3 . 7513 q The present value of a single future sum of $133. 10 three years from now, at a 10% rate of return, is $100. q By locating the intersecting point of 3 years and 10% on Table 20 -1, a factor of. 7513 is 19 found.

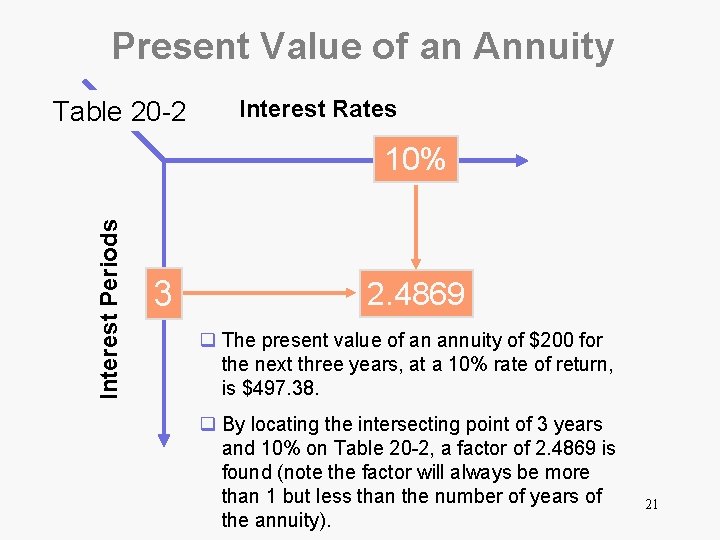
Present Value of an Annuity q An annuity is a series of equal periodic future cash flows such as projecting that a new mixing machine purchased today by Unlimited Decadence will require $200 in maintenance at the end of the next 3 years. q The present value of an annuity, then, is the amount of money that, if invested at some interest rate today, will generate a set number of equal periodic payments (receipts) that are made over equal time intervals in the future. q Present value tables can be used to calculate these amounts. 20

Present Value of an Annuity Table 20 -2 Interest Rates Interest Periods 10% 3 2. 4869 q The present value of an annuity of $200 for the next three years, at a 10% rate of return, is $497. 38. q By locating the intersecting point of 3 years and 10% on Table 20 -2, a factor of 2. 4869 is found (note the factor will always be more than 1 but less than the number of years of the annuity). 21

Net Present Value Method q The net present value method is one approach to evaluating capital expenditure proposals. It considers the time value of money and involves the following three steps: 1. Determine the initial expected cash payment required. 2. Determine the present value of the expected future net cash receipts. 3. Determine the net present value (difference between step 1 and 2). 22

Net Present Value Method – Operating Rules q The decision rules relating to the computation of net present value are set forth below. NPV is Zero, then ROR = RROR Acceptable NPV Negative, then ROR < RROR Not Acceptable NPV is Positive, then ROR > RROR Acceptable Where ROR = Rate of return calculated on investment and RROR = Required return (cutoff rate) by decision-makers 23

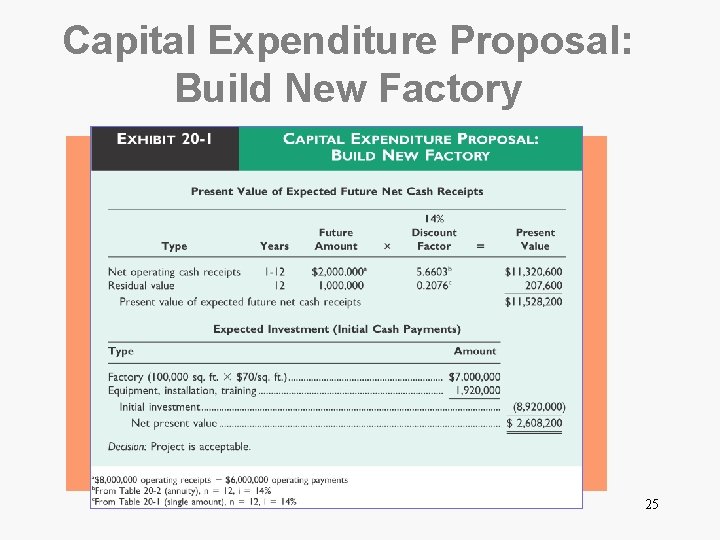
Net Present Value Illustration q Lets assume Unlimited Decadence is considering building a new factory costing $7, 000. Equipment, installation, and training costs are expected to be $1, 920, 000. q The company estimates the factory can be used for 12 years and could be sold for $1, 000 million (residual value). q Depreciation on the plant is $660, 000 per year and is expected to increase operating revenues by $8, 000 and operating expenses (other than depreciation by $6, 660, 000. q Unlimited Decadence’s cost of capital (required rate of return) is 14%. 24

Capital Expenditure Proposal: Build New Factory 25

Net Present Value Illustration q Lets now assume Unlimited Decadence is considering replacing its existing “wrapper” machine with a new improved one. The new machine costs $30, 000 to buy and installation costs are expected to $500. The old machine could be sold for $400. q The new machine is expected to have a 4 year useful life after which it could be sold for $1, 000 (residual value). q The new machine is expected to save $10, 000 per year in employee labor costs. q Unlimited Decadence’s cost of capital (required rate of return) is 14%. 26

Capital Expenditure Proposal: Purchase Wrapper Machine 27

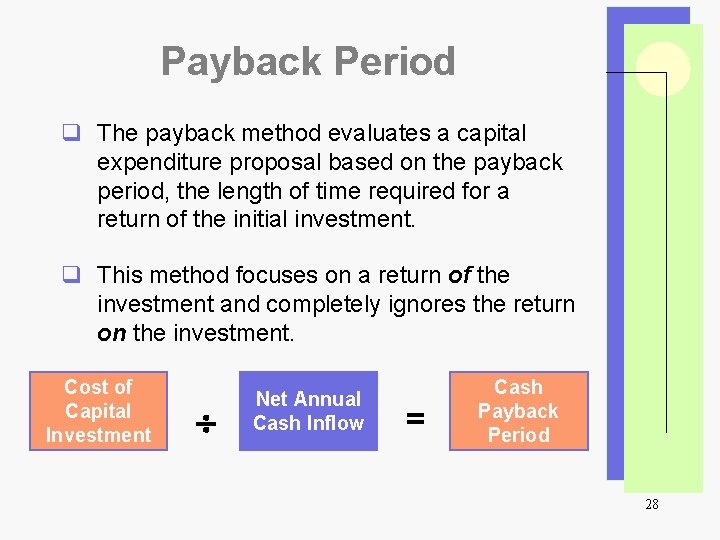
Payback Period q The payback method evaluates a capital expenditure proposal based on the payback period, the length of time required for a return of the initial investment. q This method focuses on a return of the investment and completely ignores the return on the investment. Cost of Capital Investment Net Annual Cash Inflow = Cash Payback Period 28

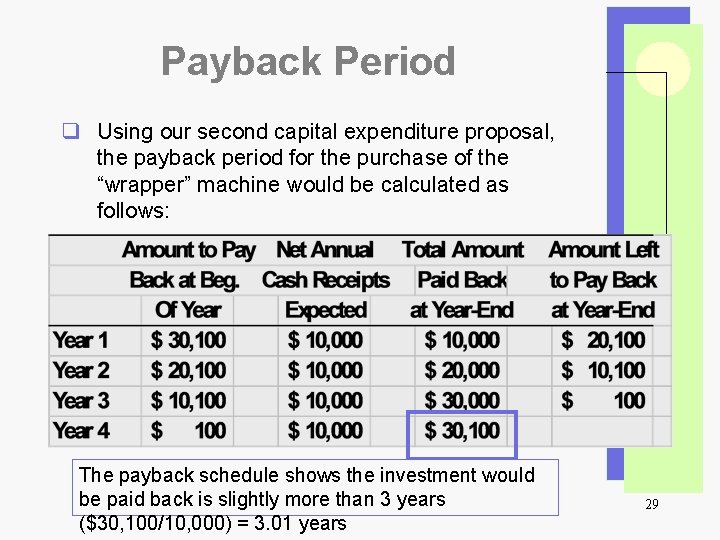
Payback Period q Using our second capital expenditure proposal, the payback period for the purchase of the “wrapper” machine would be calculated as follows: The payback schedule shows the investment would be paid back is slightly more than 3 years ($30, 100/10, 000) = 3. 01 years 29

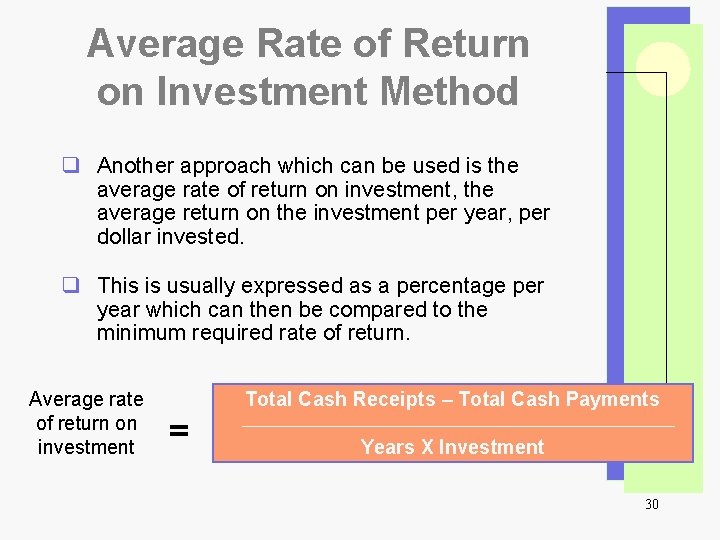
Average Rate of Return on Investment Method q Another approach which can be used is the average rate of return on investment, the average return on the investment per year, per dollar invested. q This is usually expressed as a percentage per year which can then be compared to the minimum required rate of return. Average rate of return on investment Total Cash Receipts – Total Cash Payments = Years X Investment 30

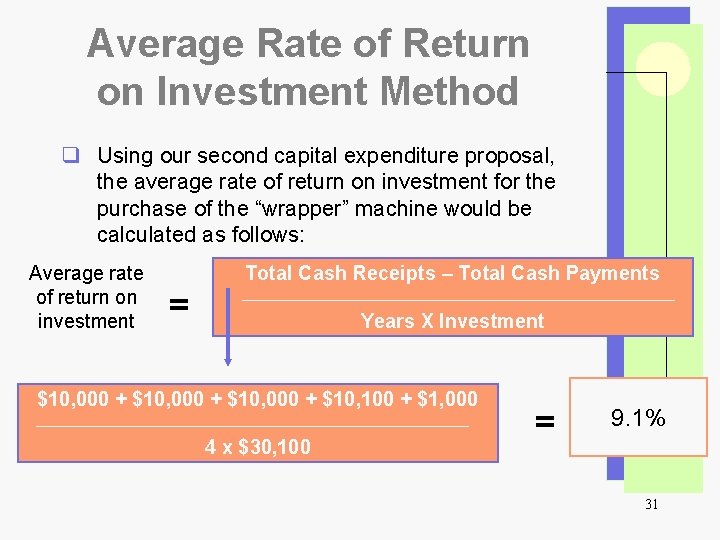
Average Rate of Return on Investment Method q Using our second capital expenditure proposal, the average rate of return on investment for the purchase of the “wrapper” machine would be calculated as follows: Average rate of return on investment Total Cash Receipts – Total Cash Payments = Years X Investment $10, 000 + $10, 100 + $1, 000 4 x $30, 100 = 9. 1% 31

Average Rate of Return on Investment Method q In contract to the payback period method, the average rate of return method does consider the return on investment. q However, this method does not take into account the time value of money, so it has disadvantages like the payback period method. q It does not provide a good basis for making a capital investment decision. 32

Mutually Exclusive Proposals q Sometimes there are several alternatives that may achieve the company’s desired objectives. q Most proposals are mutually exclusive, meaning if proposal A is chosen then proposal B is rejected. q If more than one proposal has a positive net present value and assuming other factors are equal, the company will likely choose the one with the highest value since it reflects the highest rate of return. 33

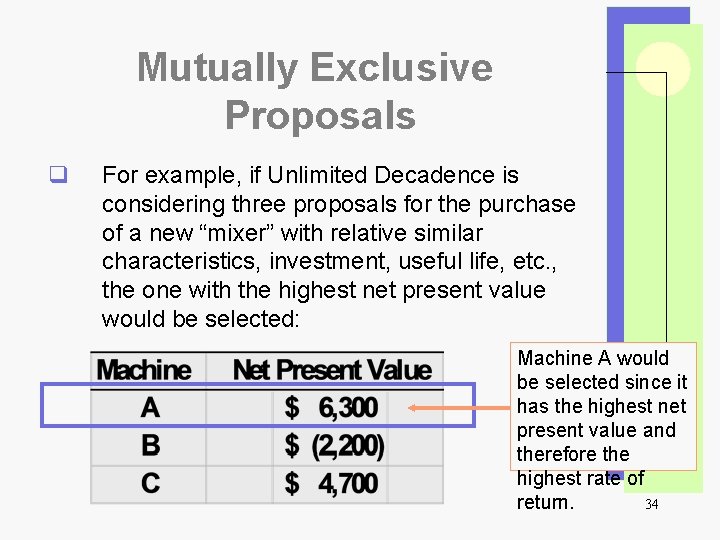
Mutually Exclusive Proposals q For example, if Unlimited Decadence is considering three proposals for the purchase of a new “mixer” with relative similar characteristics, investment, useful life, etc. , the one with the highest net present value would be selected: Machine A would be selected since it has the highest net present value and therefore the highest rate of return. 34

Capital Rationing q If a company has enough cash available, all acceptable capital expenditure proposals could be made. q However, cash is usually a scarce resource and a company may not be able to finance everything to meet the company’s objectives. q Capital rationing occurs when a company cannot obtain sufficient cash to make all of the investments that it would like to make. 35

Capital Rationing q For example, suppose Unlimited Decadence has $200, 000 for capital expenditures in the current budget period. Each of the following proposal achieves a different, but important objective for the company. Which one should they accept? Proposal A could be accepted but this would use all of the budgeted resources. However, proposals B and C could be selected because they achieve two objectives and together have a higher net present value that proposal A. This become a matter of priorities. 36