Chapter 2 Updated 10292020 Time reversal Xt Time











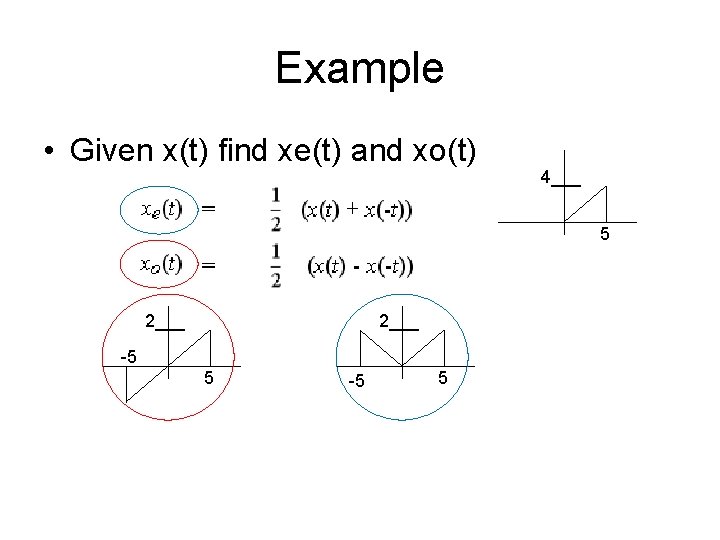




![Product of periodic Signals X(t) = xa(t) * Xb(t) = = 2 sin[t(7 p/24)]* Product of periodic Signals X(t) = xa(t) * Xb(t) = = 2 sin[t(7 p/24)]*](https://slidetodoc.com/presentation_image/24656c0c4d4a1a9865644d9ff579e956/image-29.jpg)



















- Slides: 62

Chapter 2 Updated 10/29/2020

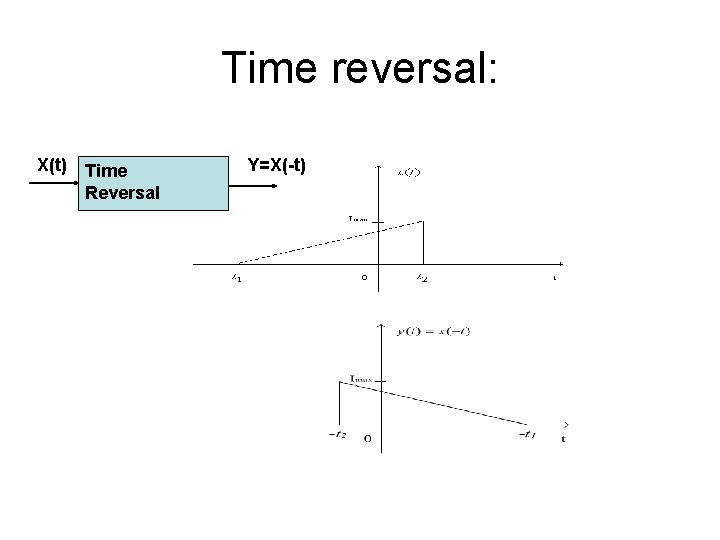
Time reversal: X(t) Time Reversal Y=X(-t)

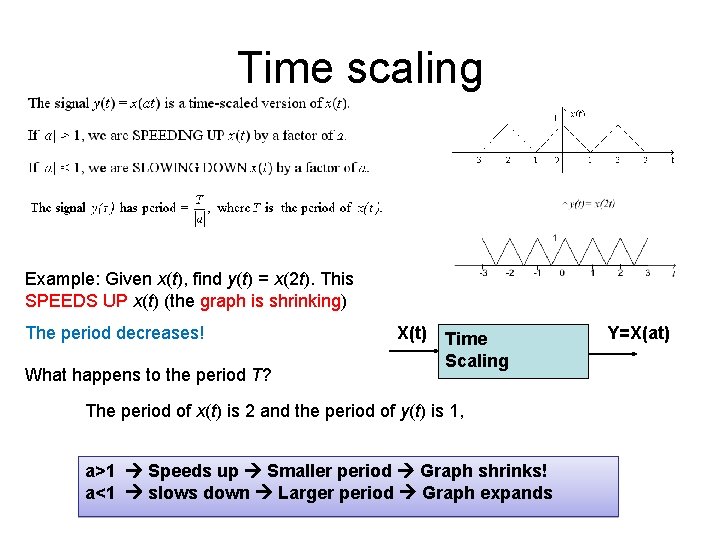
Time scaling Example: Given x(t), find y(t) = x(2 t). This SPEEDS UP x(t) (the graph is shrinking) The period decreases! What happens to the period T? X(t) Time Scaling The period of x(t) is 2 and the period of y(t) is 1, a>1 Speeds up Smaller period Graph shrinks! a<1 slows down Larger period Graph expands Y=X(at)

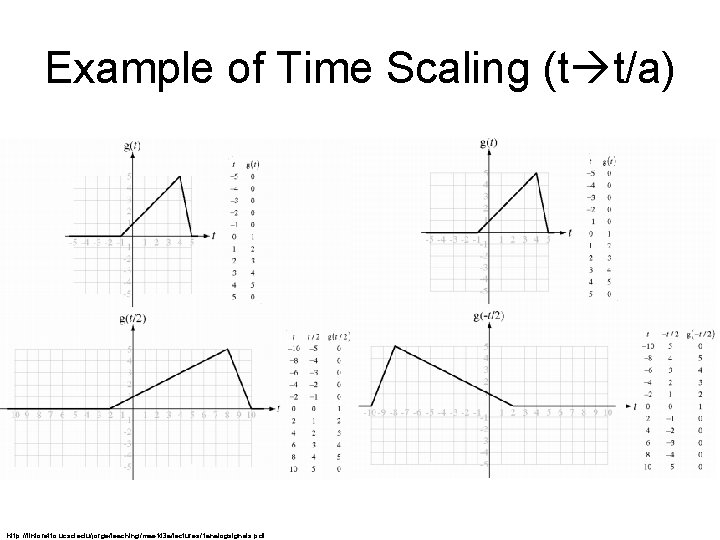
Example of Time Scaling (t t/a) http: //tintoretto. ucsd. edu/jorge/teaching/mae 143 a/lectures/1 analogsignals. pdf

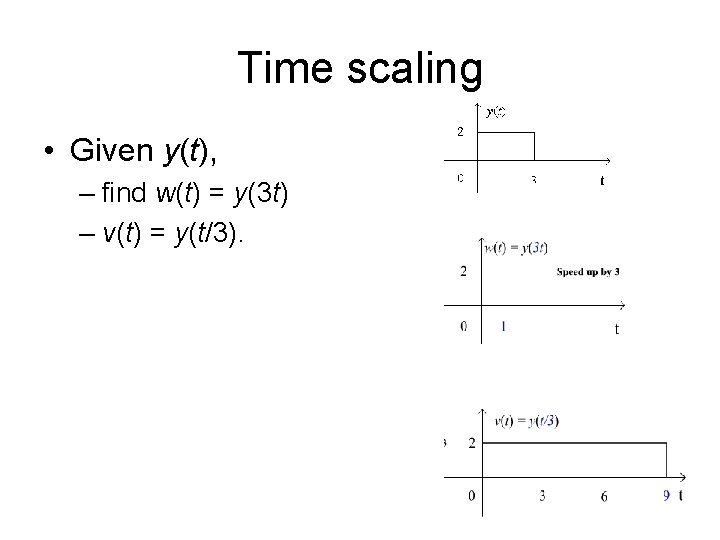
Time scaling • Given y(t), – find w(t) = y(3 t) – v(t) = y(t/3).

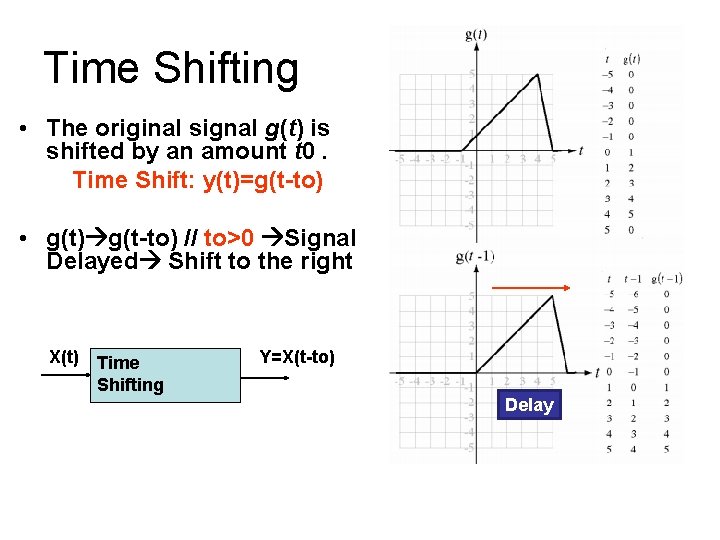
Time Shifting • The original signal g(t) is shifted by an amount t 0. Time Shift: y(t)=g(t-to) • g(t) g(t-to) // to>0 Signal Delayed Shift to the right X(t) Time Shifting Y=X(t-to) Delay

Time Shifting X(t) • The original signal x(t) is shifted by an amount t 0. Time Shift: y(t)=x(t-to) • X(t) X(t-to) // to>0 Signal Delayed Shift to the right • X(t) X(t+to) // to<0 Signal Advanced Shift to the left Time Shifting Y=X(t-to)

Time Shifting Example • Given x(t) = u(t+2) -u(t-2), – find • x(t-t 0)= • x(t+t 0)= Answer: • x(t-t 0)= u(t-to+2) -u(t-to-2), • x(t+t 0)= u(t+to+2) -u(t+to-2), But how can we draw this function?

Note: Unit Step Function a discontinuous-time signal

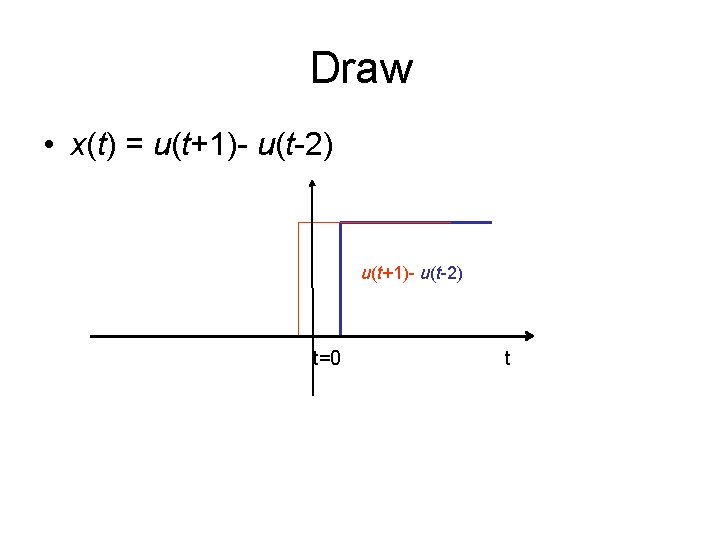
Draw • x(t) = u(t+1)- u(t-2) t=0 t

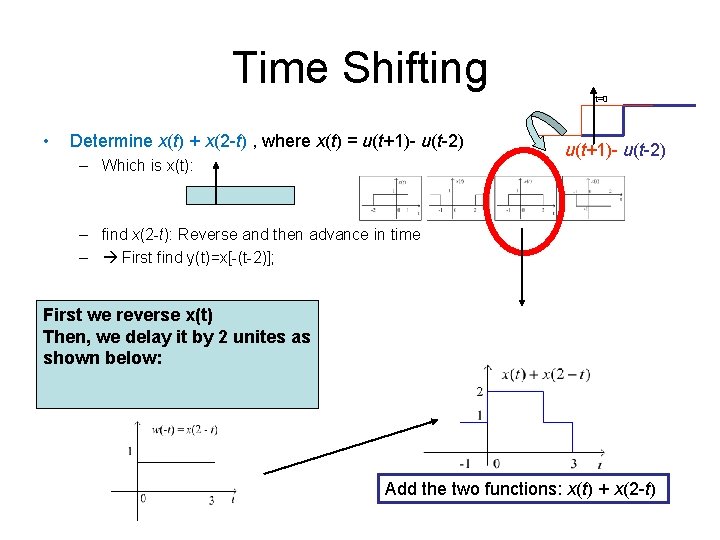
Time Shifting t=0 • Determine x(t) + x(2 -t) , where x(t) = u(t+1)- u(t-2) – Which is x(t): u(t+1)- u(t-2) – find x(2 -t): Reverse and then advance in time – First find y(t)=x[-(t-2)]; First we reverse x(t) Then, we delay it by 2 unites as shown below: Add the two functions: x(t) + x(2 -t)

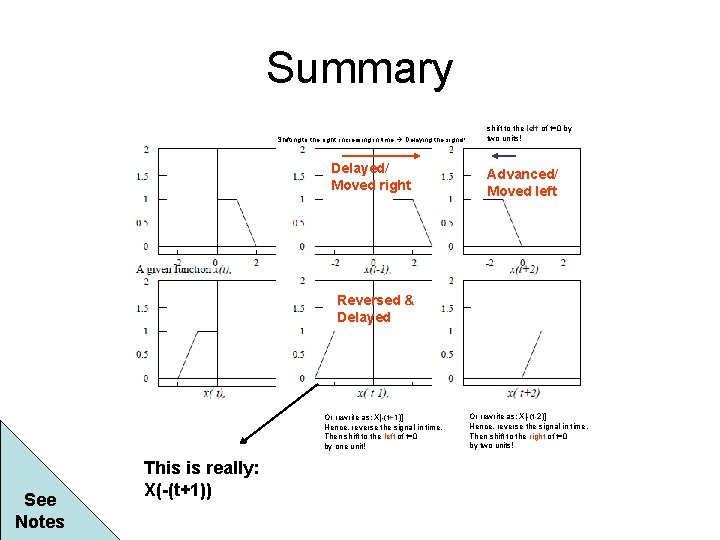
Summary Shifting to the right; increasing in time Delaying the signal! Delayed/ Moved right shift to the left of t=0 by two units! Advanced/ Moved left Reversed & Delayed Or rewrite as: X[-(t+1)] Hence, reverse the signal in time. Then shift to the left of t=0 by one unit! See Notes This is really: X(-(t+1)) Or rewrite as: X[-(t-2)] Hence, reverse the signal in time. Then shift to the right of t=0 by two units!

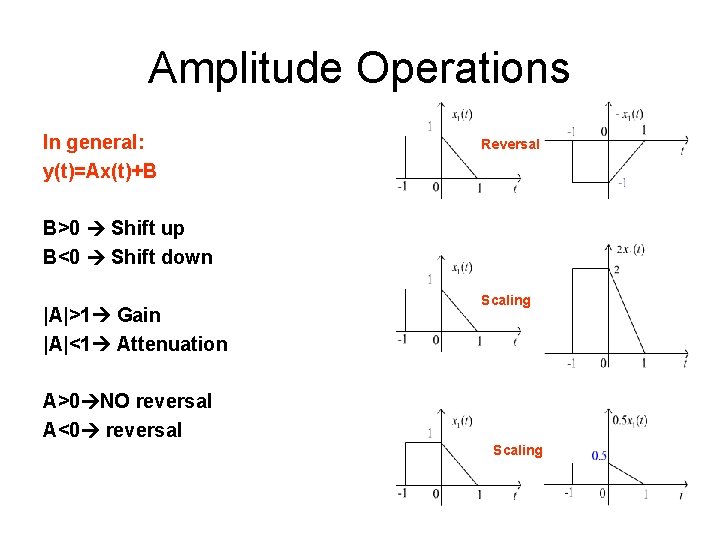
Amplitude Operations In general: y(t)=Ax(t)+B Reversal B>0 Shift up B<0 Shift down |A|>1 Gain |A|<1 Attenuation Scaling A>0 NO reversal A<0 reversal Scaling

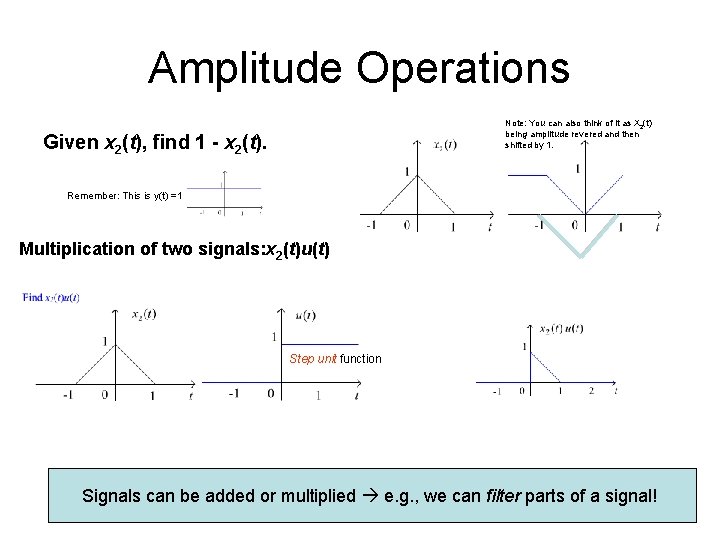
Amplitude Operations Given x 2(t), find 1 - x 2(t). Remember: This is y(t) =1 Ans. Multiplication of two signals: x 2(t)u(t) Step unit function Signals can be added or multiplied Ans.

Amplitude Operations Note: You can also think of it as X 2(t) being amplitude revered and then shifted by 1. Given x 2(t), find 1 - x 2(t). Remember: This is y(t) =1 Multiplication of two signals: x 2(t)u(t) Step unit function Signals can be added or multiplied e. g. , we can filter parts of a signal!

Signal Characteristics • Even and odd signals 1. X(t) = Xe(t) + Xo(t) 2. X(-t) = X(t) Even 3. X(-t) = -X(t) Odd • Represent Xo(t) in terms of X(t) only! Represent Xe(t) in terms of X(t) only! Properties Xe + Ye = Ze Xo + Yo = Zo Xe + Yo = Ze + Zo Xe * Ye = Ze Xo * Yo = Ze Xe * Yo = Zo

Signal Characteristics • Even and odd signals 1. X(t) = Xe(t) + Xo(t) 2. X(-t) = X(t) Even 3. X(-t) = -X(t) Odd • Properties Xe + Ye = Ze Xo + Yo = Zo Xe + Yo = Ze + Zo Know These! Xe * Ye = Ze Xo * Yo = Ze Xe * Yo = Zo

Proof Examples • Prove that product of two even signals is even. • Prove that product of two odd signals is odd. • What is the product of an even signal and an odd signal? Prove it! Change t -t

Signal Characteristics: Find uo(t) and ue(t) Remember: Given:

Signal Characteristics Symmetric across the vertical axis Anti-symmetric across the vertical axis

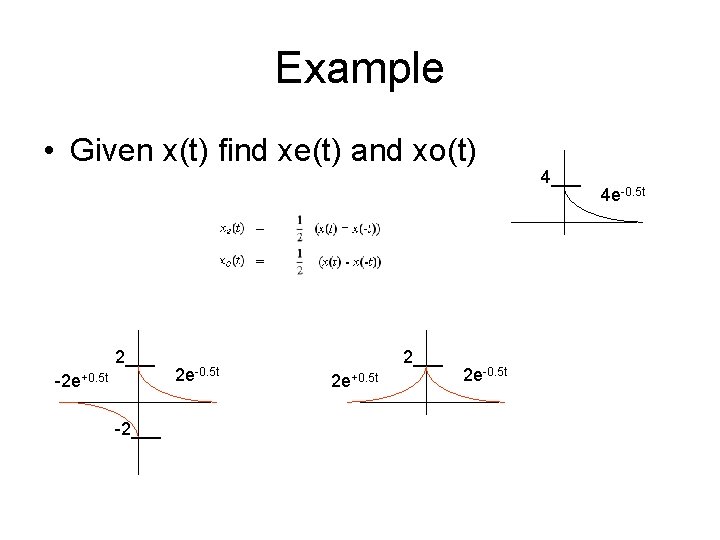
Example • Given x(t) find xe(t) and xo(t) 4___ 5 2___ 5 5
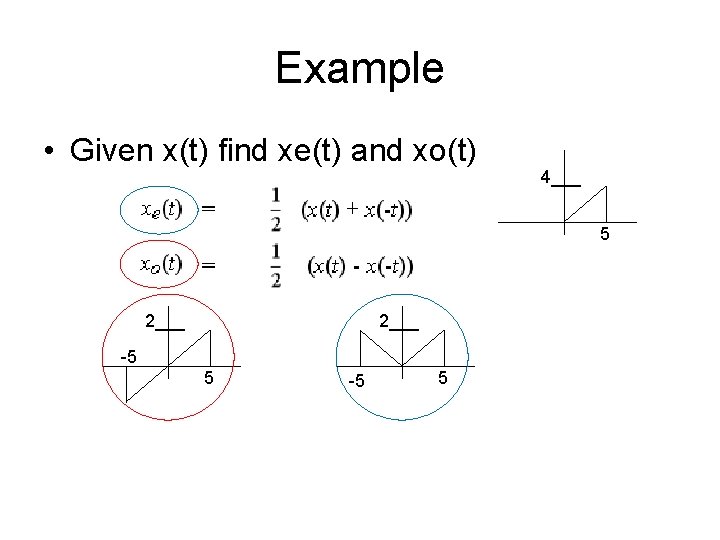
Example • Given x(t) find xe(t) and xo(t) 4___ 5 2___ -5 5

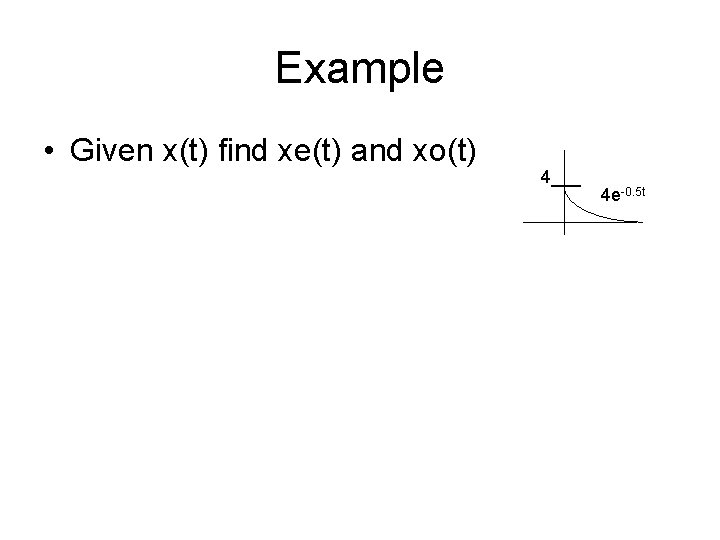
Example • Given x(t) find xe(t) and xo(t) 2___ 2 e-0. 5 t 5 -2___ 2 e+0. 5 t 2___ 5 2 e-0. 5 t 4___ 4 e-0. 5 t

Example • Given x(t) find xe(t) and xo(t) 2___ 2 e-0. 5 t 5 -2 e+0. 5 t -2___ 2 e+0. 5 t 2___ 5 2 e-0. 5 t 4___ 4 e-0. 5 t

Periodic and Aperiodic Signals • Given x(t) is a continuous-time signal • X (t) is periodic iff X(t) = x(t+n. T) for any T and any integer n • Example – Is X(t) = A cos(wt) periodic? • X(t+n. T) = A cos(w(t+Tn)) = • A cos(wt+w 2 np)= A cos(wt) – Note: f 0=1/T 0; wo=2 p/To <= Angular freq. – T 0 is fundamental period; T 0 is the minimum value of T that satisfies X(t) = x(t+T)

Periodic signals Examples: • =>Show that sin(t) is in fact a periodic signal. • Use a graph • Show it mathematically – What is the period? – Is this an even or odd signal? • =>Is tesin(t) periodic? – X(t) = x(t+T)?

Sum of periodic Signals • • X(t) = x 1(t) + X 2(t) X(t+n. T) = x 1(t+m 1 T 1) + X 2(t+m 2 T 2) m 1 T 1=m 2 T 2 = To = Fundamental period Example: – cos(tp/3)+sin(tp/4) – T 1=(2 p)/(p/3)=6; T 2 =(2 p)/(p/4)=8; – T 1/T 2=6/8 = ¾ = (rational number) = m 2/m 1 – m 1 T 1=m 2 T 2 Find m 1 and m 2 – 6. 4 = 3. 8 = 24 = To (n=1)

Sum of periodic Signals • • Note that T 1/T 2 must be RATIONAL (ratio of integers) X(t) = x 1(t) + X 2(t) X(t+n. T) = x 1(t+m 1 T 1) + X 2(t+m An irrational 2 T number 2) is any real number which cannot be m 1 T 1=m 2 T 2 = To=Fundamental expressed asperiod a fraction a/b, where a and b are integers, with b non-zero. Example: – cos(tp/3)+sin(tp/4) – T 1=(2 p)/(p/3)=6; T 2 =(2 p)/(p/4)=8; – T 1/T 2=6/8 = ¾ – m 1 T 1=m 2 T 2 T 1/T 2= m 2/m 1 6/8=3/4 6. 4 = 3. 8 24 = To Read about Irrational Numbers: http: //www. mathsisfun. com/irrational-numbers. html
![Product of periodic Signals Xt xat Xbt 2 sint7 p24 Product of periodic Signals X(t) = xa(t) * Xb(t) = = 2 sin[t(7 p/24)]*](https://slidetodoc.com/presentation_image/24656c0c4d4a1a9865644d9ff579e956/image-29.jpg)
Product of periodic Signals X(t) = xa(t) * Xb(t) = = 2 sin[t(7 p/24)]* cos[t(p/24)]; find the period of x(t) • We know: = 2 sin[t(7 p/12)/2]* cos[t(p/12)/2]; – Using Trig. Itentity: • x(t) = sin(tp/3)+sin(tp/4) • Thus, To=24 , as before! http: //www. sosmath. com/trig/Trig 5/trig 5/pdf. html

Sum of periodic Signals – may not always be periodic! – – T 1=(2 p)/(1)= 2 p; T 2 =(2 p)/(sqrt(2)); T 1/T 2= sqrt(2); Note: T 1/T 2 = sqrt(2) is an irrational number – X(t) is aperiodic Note that T 1/T 2 is NOT RATIONAL (ratio of integers) In this case!

Sum of periodic Several Signals • Example – X 1(t) = cos(3. 5 t) – X 2(t) = sin(2 t) – X 3(t) = 2 cos(t 7/6) – Is v(t) = x 1(t) + x 2(t) + x 3(t) periodic? – What is the fundamental period of v(t)? – Find even and odd parts of v(t). Do it on your own!

Sum of periodic Signals (cont. ) – – – X 1(t) = cos(3. 5 t) f 1 = 3. 5/2 p T 1 = 2 p /3. 5 X 2(t) = sin(2 t) f 2 = 2/2 p T 2 = 2 p /2 X 3(t) = 2 cos(t 7/6) f 3 = (7/6)/2 p T 3 = 2 p /(7/6) T 1/T 2 = 4/7 Ratio or two integers T 1/T 3 = 1/3 Ratio or two integers Summation is periodic T 1 2 p/3. 5 T 2 2 p/2 T 3 12 p/7 m 1 7. 3=21 m 2 2. 6=12 m 3 m 1 x. T 1 12 p m 2 x. T 2 12 p m 3 x. T 3 12 p – m 1 T 1 = m 2 T 2 = m 3 T 3 = To ; Hence we find To – The question is how to choose m 1, m 2, m 3 such that the above relationship holds – We know: 7(T 1) = 4(T 2) & 3(T 1) = 1(T 3) ; m 1(T 1)=m 2(T 2) – Hence: 21(T 1) = 12(T 2)= 7(T 3); Thus, fundamental period: To = 21(T 1) = 21(2 p /3. 5)=12(T 2)=12 p Find even and odd parts of v(t). 7. 1=7

Important Engineering Signals • Euler’s Formula (polar form or complex exponential form) – Remember: ej. F = 1|_F and arg [ ej. F ] = F (can you prove these? ) notes • Unit Step Function (Singularity Function) notes What is sin(A+B)? Or cos(A+B)? • Use Unit Step Function to express a block function (window) -T/t notes

Important Engineering Signals • Euler’s Formula notes • Unit Step Function (Singularity Function) – Can you draw x(t) = cos(t)[u(t) – u(t-2 p)]? notes • Use Unit Step Function to express a block function (window) Next -T/2

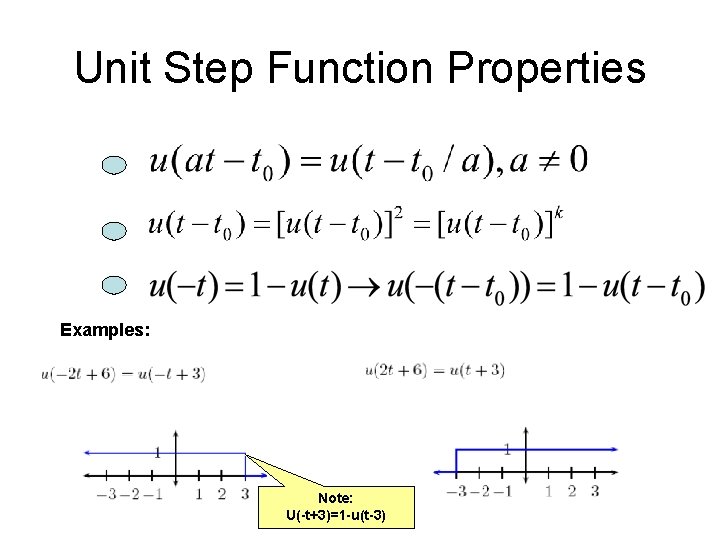
Unit Step Function Properties Examples: Note: U(-t+3)=1 -u(t-3)

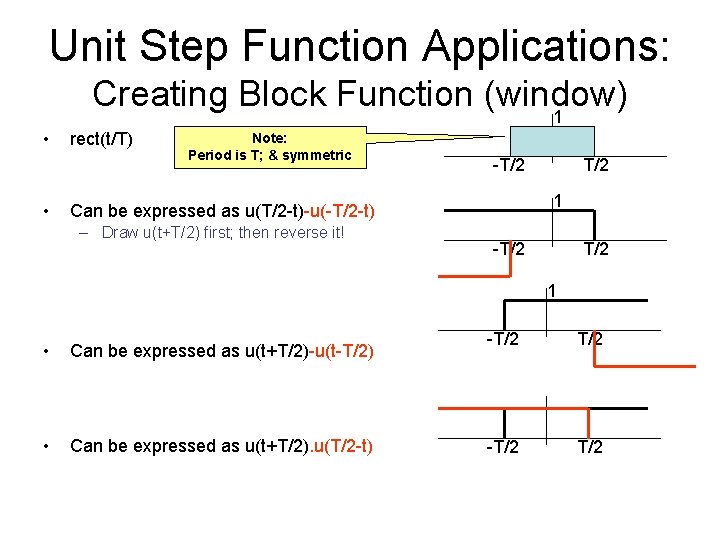
Unit Step Function Applications: Creating Block Function (window) 1 • • rect(t/T) Note: Period is T; & symmetric -T/2 1 Can be expressed as u(T/2 -t)-u(-T/2 -t) – Draw u(t+T/2) first; then reverse it! T/2 -T/2 1 • Can be expressed as u(t+T/2)-u(t-T/2) • Can be expressed as u(t+T/2). u(T/2 -t) -T/2 T/2

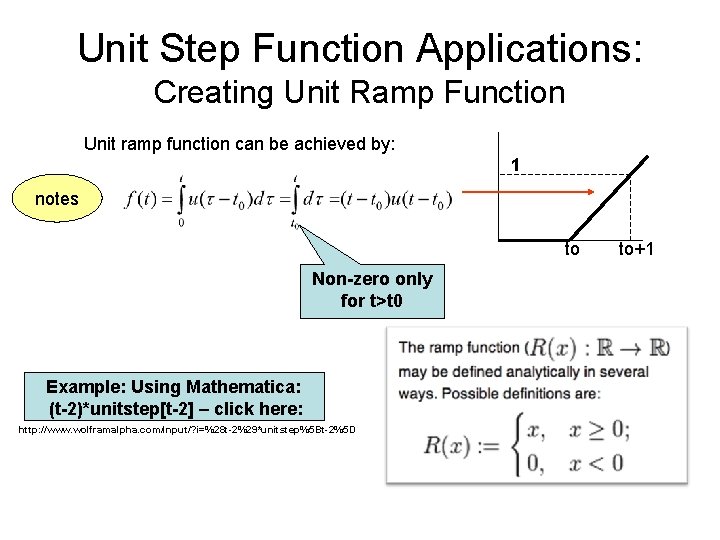
Unit Step Function Applications: Creating Unit Ramp Function Unit ramp function can be achieved by: 1 notes to Non-zero only for t>t 0 Example: Using Mathematica: (t-2)*unitstep[t-2] – click here: http: //www. wolframalpha. com/input/? i=%28 t-2%29*unitstep%5 Bt-2%5 D to+1

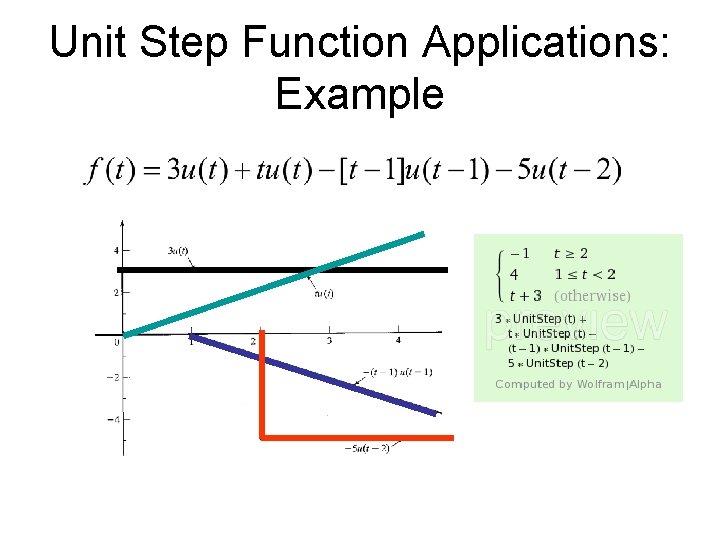
Unit Step Function Applications: Example

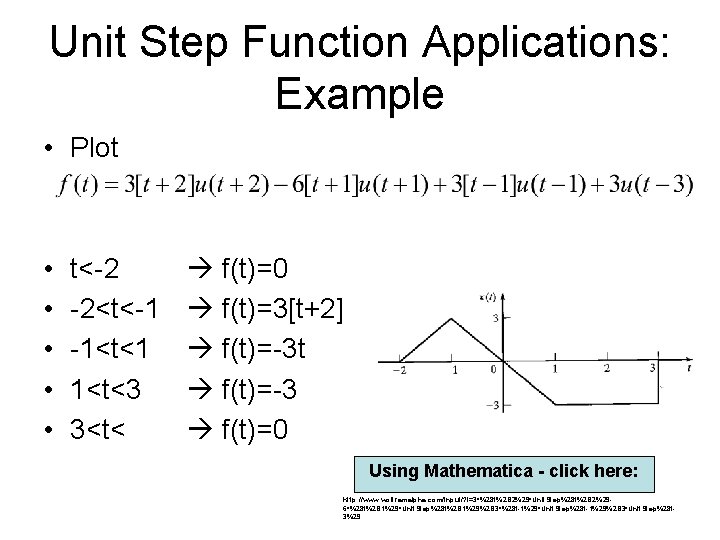
Unit Step Function Applications: Example • Plot • • • t<-2 -2<t<-1 -1<t<1 1<t<3 3<t< f(t)=0 f(t)=3[t+2] f(t)=-3 t f(t)=-3 f(t)=0 Using Mathematica - click here: http: //www. wolframalpha. com/input/? i=3*%28 t%2 B 2%29*Unit. Step%28 t%2 B 2%296*%28 t%2 B 1%29*Unit. Step%28 t%2 B 1%29%2 B 3*%28 t-1%29*Unit. Step%28 t-1%29%2 B 3*Unit. Step%28 t 3%29

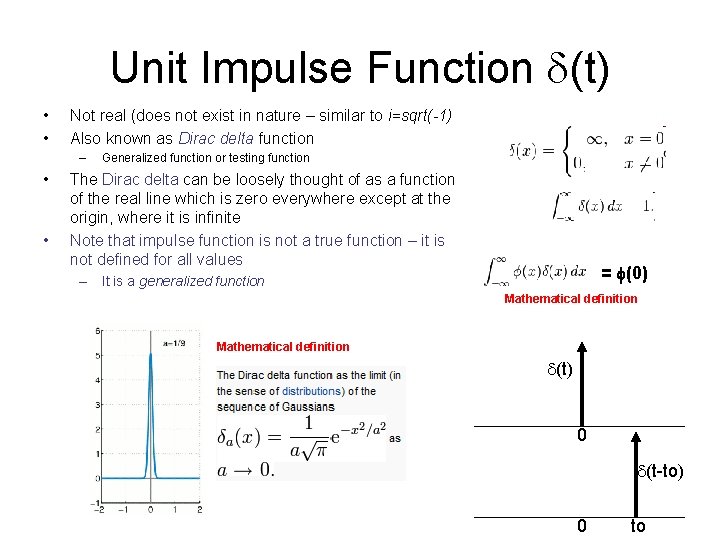
Unit Impulse Function d(t) • • Not real (does not exist in nature – similar to i=sqrt(-1) Also known as Dirac delta function – • • Generalized function or testing function The Dirac delta can be loosely thought of as a function of the real line which is zero everywhere except at the origin, where it is infinite Note that impulse function is not a true function – it is not defined for all values = f(0) – It is a generalized function Mathematical definition d(t) 0 d(t-to) 0 to

Unit Impulse Function d(t) • Also note that • Also

Unit Impulse Properties 1. Scaling – Kd(t) Area (or weight) under = K 2. Multiplication – X(t) d(t) X(0) d(t) = Area (or weight) under 3. Time Shift 1. X(t) d(t-to) X(to) d(t-to) 4. Example: Draw 3 x(t-1) d(t-3/2) where x(t)=sin(t) – Using x(t) d(t-to) X(to) d(t-to) ; 1. 3 x(3/2 -1) d(t-3/2)=3 sin(1/2) d(t-3/2)

Unit Impulse Properties • Integration of a test function – Example • Other properties: Make sure you can understand why!

Unit Impulse Properties • Example: Verify Schaum’s p 38 • Evaluate the following Schaum’s p 40 Remember:

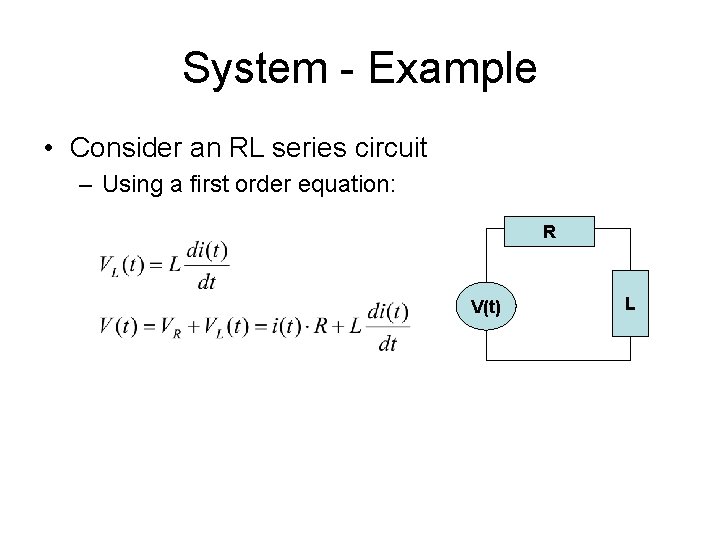
Continuous-Time Systems • A system is an operation for which causeand-effect relationship exists – Can be described by block diagrams – Denoted using transformation T[. ] • System behavior described by mathematical model X(t) T [. ] y(t)

System - Example • Consider an RL series circuit – Using a first order equation: R V(t) L

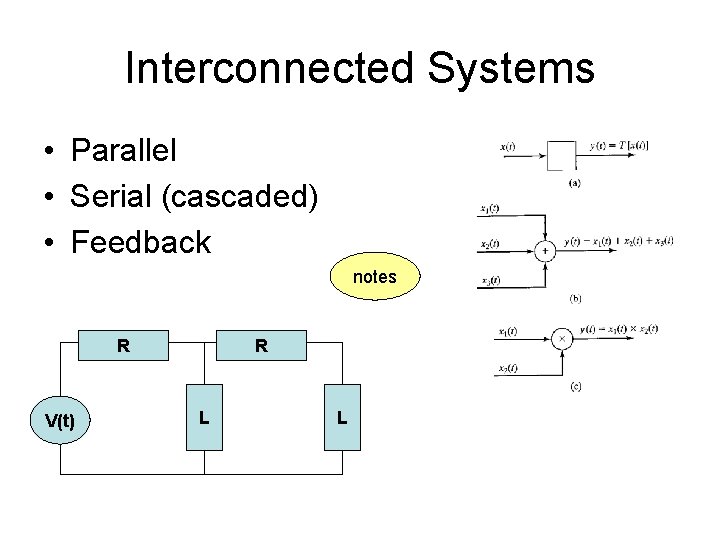
Interconnected Systems • Parallel • Serial (cascaded) • Feedback notes R V(t) R L L

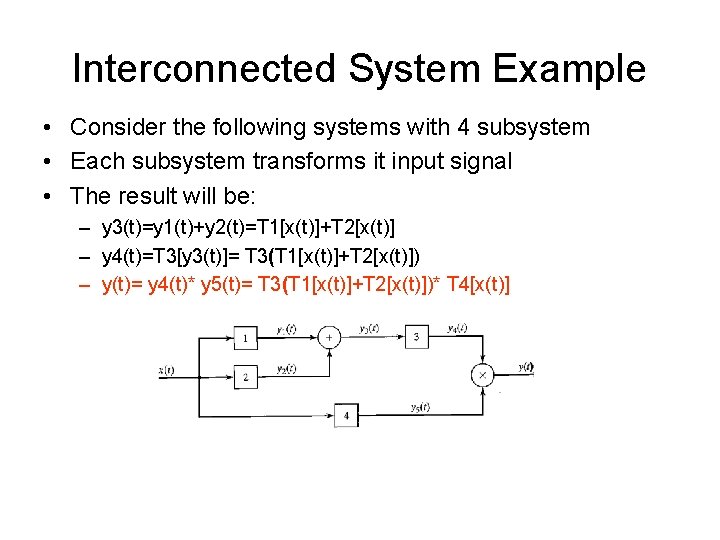
Interconnected System Example • Consider the following systems with 4 subsystem • Each subsystem transforms it input signal • The result will be: – y 3(t)=y 1(t)+y 2(t)=T 1[x(t)]+T 2[x(t)] – y 4(t)=T 3[y 3(t)]= T 3(T 1[x(t)]+T 2[x(t)]) – y(t)= y 4(t)* y 5(t)= T 3(T 1[x(t)]+T 2[x(t)])* T 4[x(t)]

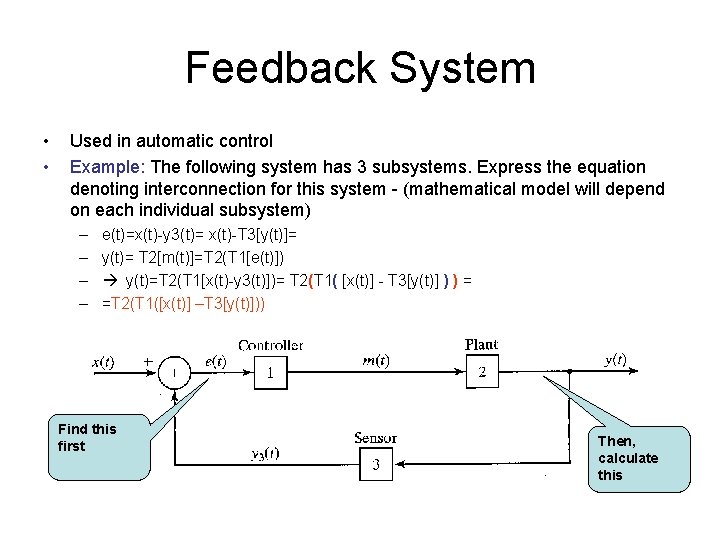
Feedback System • • Used in automatic control Example: The following system has 3 subsystems. Express the equation denoting interconnection for this system - (mathematical model will depend on each individual subsystem) – – e(t)=x(t)-y 3(t)= x(t)-T 3[y(t)]= y(t)= T 2[m(t)]=T 2(T 1[e(t)]) y(t)=T 2(T 1[x(t)-y 3(t)])= T 2(T 1( [x(t)] - T 3[y(t)] ) ) = =T 2(T 1([x(t)] –T 3[y(t)])) Find this first Then, calculate this

System Properties

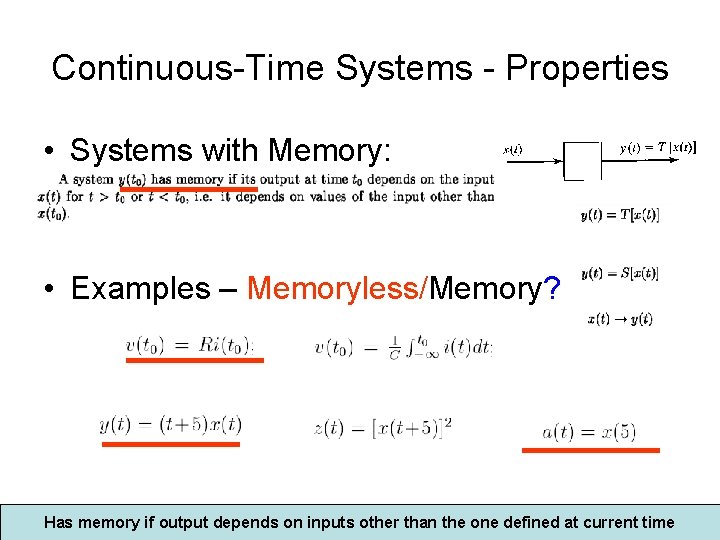
Continuous-Time Systems - Properties • Systems with Memory: • Examples – Memoryless/Memory? Has memory if output depends on inputs other than the one defined at current time

Continuous-Time Systems - Properties Inverse of a System (invertibility) Examples Noninvertible Systems Thermostat Example! (notes) Each distinct input distinct output

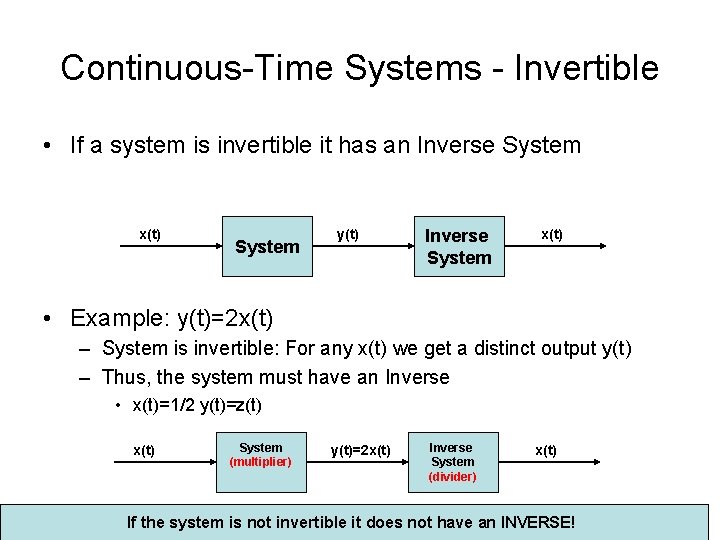
Continuous-Time Systems - Invertible • If a system is invertible it has an Inverse System x(t) System y(t) Inverse System x(t) • Example: y(t)=2 x(t) – System is invertible: For any x(t) we get a distinct output y(t) – Thus, the system must have an Inverse • x(t)=1/2 y(t)=z(t) x(t) System (multiplier) y(t)=2 x(t) Inverse System (divider) x(t) If the system is not invertible it does not have an INVERSE!

Continuous-Time Systems - Causality (non-anticipatory system) - A System can be causal with non-causal components! Examples Remember: Reverse is not TRUE! ? ? What it t<0? Depends on cause-and-effect no future dependency

Continuous-Time Systems - Stability • Many different definitions • Bounded-input-bounded-output • Example: – An ideal amplifier y(t) = 10 x(t) B 2=10 B 1 – Square system: y(t)=x^2 B 2=B 1^2 • A system can be unstable or marginally stable • More examples

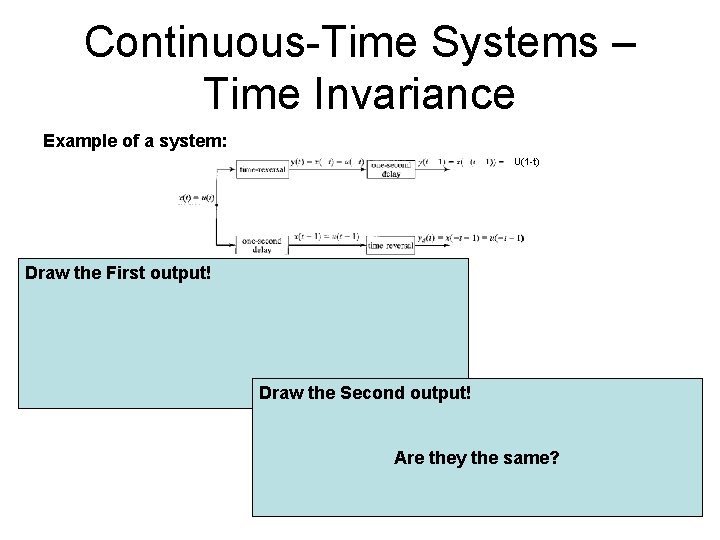
Continuous-Time Systems – Time Invariance Testing for Time Invariance To test: y(t)|t-to y(t)|x(t-to) Example: y(t) = e^x(t): y(t)|t=t-to e^x(t-to) y(t)|x(t-to) e^x(t-to) Time Invariance What if the system is time reversal? (next slide) Time-shift in input results in time-shift in output system always acts the same way (Fix System)

Continuous-Time Systems – Time Invariance Example of a system: U(1 -t) Draw the First output! Draw the Second output! Are they the same?

Continuous-Time Systems – Time Invariance Example of a system: U(1 -t) Pay attention! Due to time - reversal Time reversal operation is NOT time invariant!

Continuous-Time Systems – Time Invariance • Examples: – Do these yourself! notes

Continuous-Time Systems – Linearity • A linear system must satisfy superposition condition (additive and homogeneity hoh-muh-juh-nee-i-tee) We need to prove: a. T[x 1]+b. T[x 2]=T[a. x 1+b. x 2] • Note: for a linear system a zero input always generates an output zero • Example notes

More… • Example • Summary notes

Practice Problems • Schaum’s Outlines: – 1. 1(p 19), 1. 5(p 23). 1. 6 -1. 7(p 24)1. 16(p 30), 1. 22(p 35) – There will be more…. (check back) • Textbook: Chapter 2 - Solved Problems – 1, 3, 5 -10, 13, 14, 16, 17, 21, 22, 24, 25 -30, 33 -35, 48, 51, 53 -61