Chapter 2 TwoVariable Regression Analysis Some Basic Ideas

Chapter 2. Two-Variable Regression Analysis: Some Basic Ideas A Hypothetical Example Imagine a hypothetical country with a total population of 60 families. Question: To set a relationship between weekly family consumption expenditure (Y) and weekly family income (X).

Conditional Distribution of Y with respect to X Table gives the distribution of consumption expenditure Y corresponding What 2. 1 is Conditional Mean? How do you calculate it? Conditional Mean Y given 55(1/5)+60(1/5)+65(1/5)+70(1/5)+75(1/5) to a fixed level offor income X; that. X=80: is conditional distribution of Y conditional = 65 upon the given values of X.

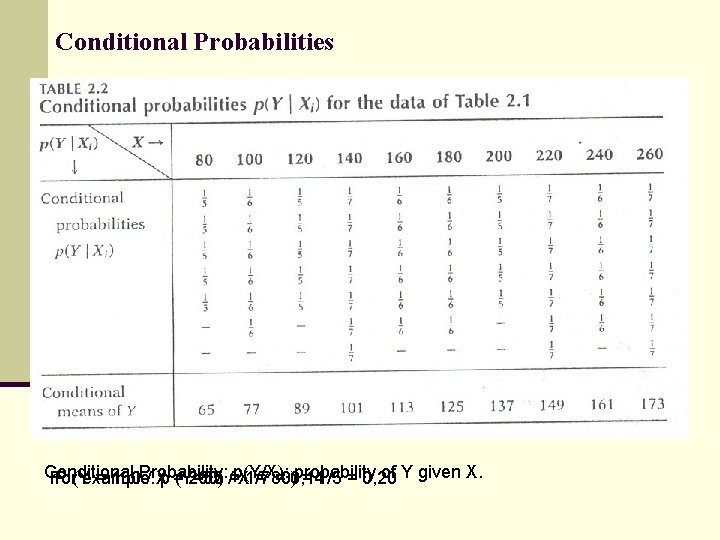
Conditional Probabilities Conditional probability of Y given X. For P (Yexample: = 150 Probability: / Xp =(Y=55 260) /=p(Y/X): X 1/7 = 80) = 0, 14 = 1/5 = 0, 20

Conditional Mean or Conditional Expectation E (Y / X = Xi) It is read as “the expected value of Y given that X takes the specific value Xi”

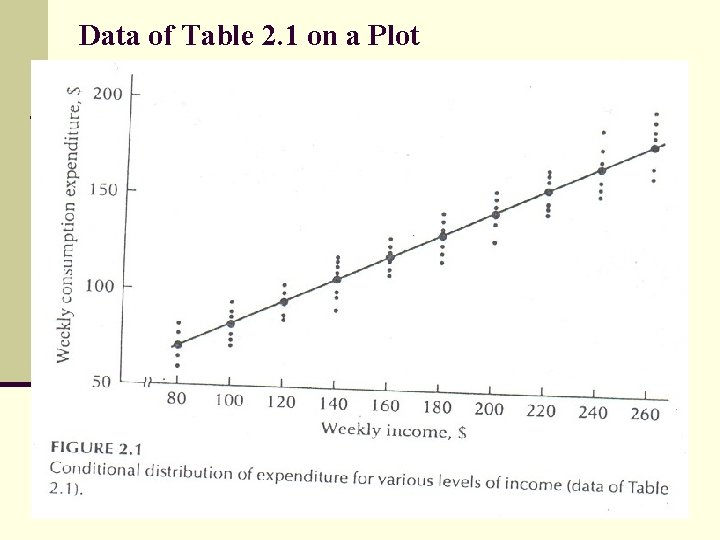
Data of Table 2. 1 on a Plot

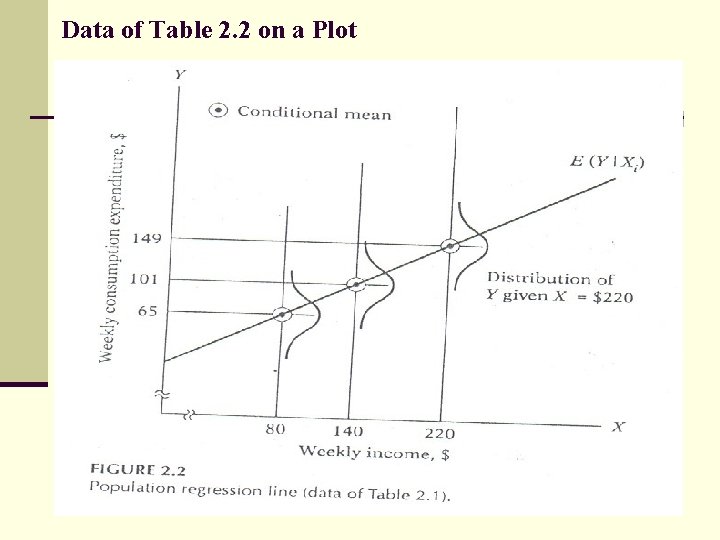
Data of Table 2. 2 on a Plot

The Concept of Population Regression Function (PRF) n If E (Y / X = Xi), n then Therefore, n E (Y / Xi) = f (Xi) PRF That is, if conditional mean of Y depends on each level of X variable, then conditional mean of Y is said to be a function of given X values.

On PRF More PRF is E (Y / Xi) = f (Xi) Therefore, PRF is also linear function of Xi, that is: E (Y / Xi) = 1 + 2 Xi Where 1 and 2 are unknown parameters known as the regression coefficients.

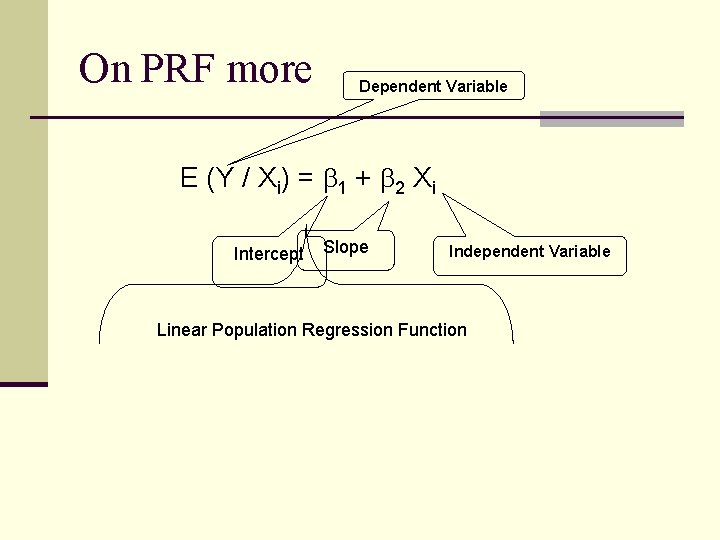
On PRF more Dependent Variable E (Y / Xi) = 1 + 2 Xi Intercept Slope Independent Variable Linear Population Regression Function

Stochastic Specification of PRF E (Y / Xi) = 1 + 2 Xi ui = Yi – E (Y/Xi) Expected Actual value of Y or estimated value of Yi =Stochastic E (Y/XError )i + Term ui Y with respect to X Then, Yi = 1 + 2 X i + u i

Stochastic Error Term E ( Yi / X) = E [E( Y / Xi)] + E (ui /Xi) E ( Yi / X) = E( Y / Xi) + E (ui /Xi) = 0 Therefore, E ( Yi / X) = E( Y / Xi)

The Sample Regression Function (SRF) PRF: Yi = 1 + 2 X i + u i SRF: of 2 Estimator of 1

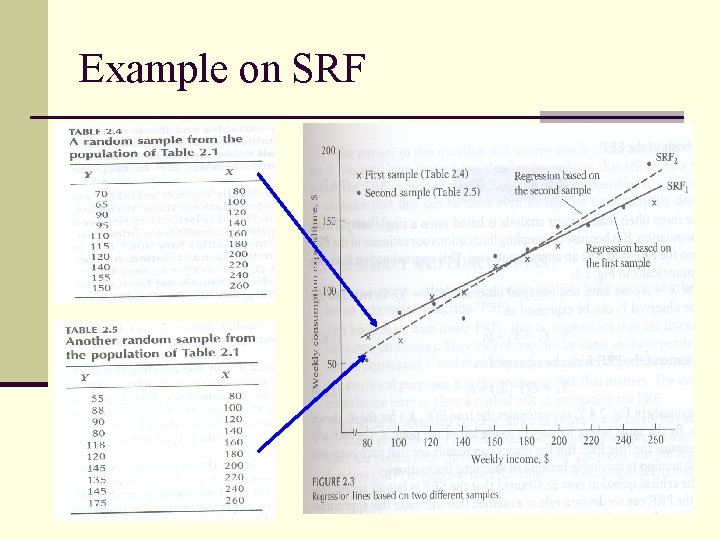
Example on SRF

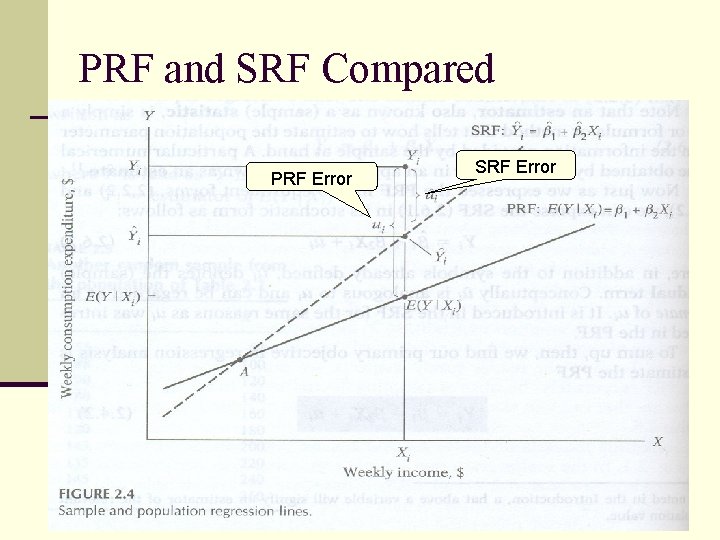
PRF and SRF Compared PRF Error SRF Error