Chapter 2 Syntax and meaning of prolog programs
























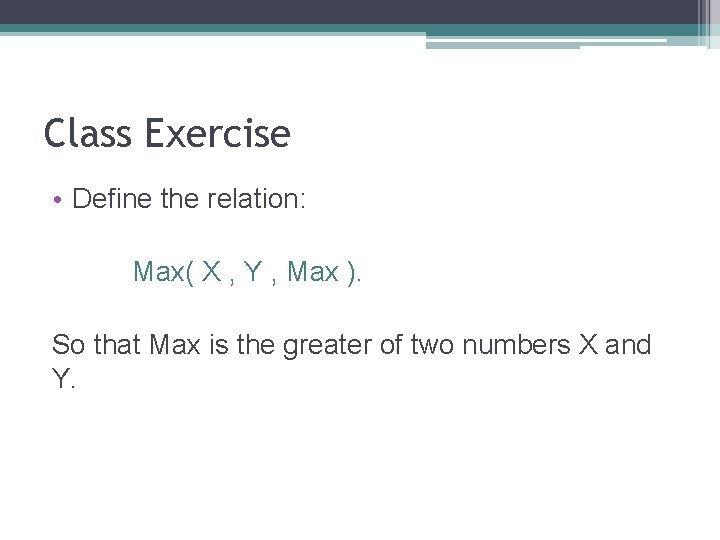
- Slides: 28

Chapter 2 Syntax and meaning of prolog programs Part 1

Arithmetic Operations • Prolog is mainly a language for symbolic computation. • Some of the predefined operators can be used for basic arithmetic operations : • • Addition ( + ) Subtraction ( - ) Multiplication ( * ) Division ( / ) Division - integer result - ( // ) Power ( ** ) Modulation ( mod )

“ is “ Operator • we can get the answers of the arithmetic questions by using variables. Var_name is Expression • The left argument of the is operator is a simple object (variable and number) , the right argument is an arithmetic expression.

Arithmetic Operations Arithmetic Prolog 2+3=5 3 x 4 = 12 5– 3=2 3 – 5 = -2 4/2=2 1 is the remainder when 7 is divided by 2 ? - 5 is 2+3. ? - 12 is 3 4. ? - 2 is 5 -3. ? - -2 is 3 -5. ? - 2 is 4/2. ? - 1 is mod(7, 2).

Arithmetic Operations Example: ? - X = 1 + 2. ? - X is 5/2 , Y is 2 -6 , Z is 5 mod 2. ? - X is (14 + 16)/3 , X + 3 = Y.

Arithmetic Operations • Arithmetic operations also uses comparing numerical values. • The comparison operators are as follows: =: = == < > >= =< Equal. Not equal. Less than. Greater than or equal to. Less than or equal to.

Arithmetic Operations Example: ? - 277*37 > 10000. ? - 1+2 = 2+1 ? - 1+2 =: = 2+1 ? - X+4 == 5+7

Matching • The most important operation on terms is Matching. • Two terms are matching when they are equivalent to each other. • To request Prolog matching operation, we use ‘=‘ : Expression 1 = Expression 2 • Matching is a process that takes as inputs two terms and check whether they match. ▫ If the terms do not match, we say this process fails. ▫ If they match, the process succeeds.

Matching • The general rules to decide whether two terms ( S and T) match are as follows: ▫ If S and T are constants , they match only if they are the same object. ▫ If S is a variable and T is anything , they match only if S is equivalent to an object in T.

Matching - examples ? - 14+15 = 14+15. ? - 2*4 = 4*2. ? - 5 = 2 + 3. ? - X+1 = 5+Y

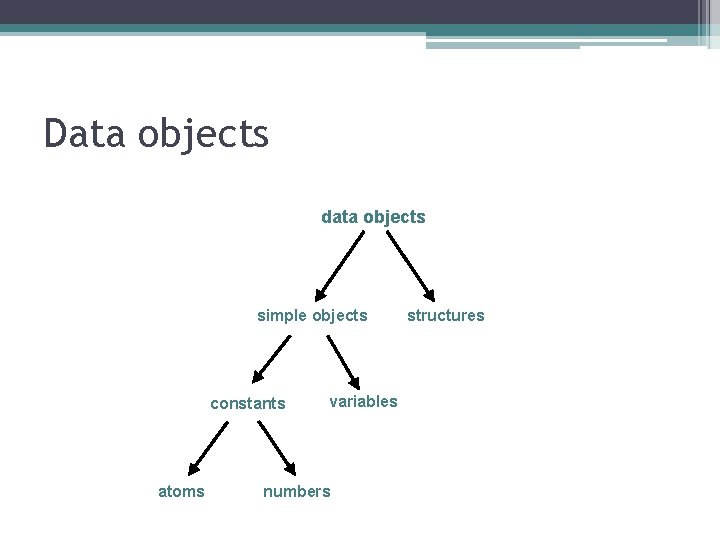
Data objects data objects simple objects constants atoms variables numbers structures

Structured Data objects ▫ A structure object is a complex data types composed of a functor and a fixed number of arguments. ▫ Syntax : Functor (arg 1, arg 2, . . . ) ▫ Example : create a structured object of this date : 1 / may / 2015 date (1, may, 2001)

Structured Data objects q To represent any day in may (assuming Day is variable) date (Day, may, 2015) ▫ All structured objects can be presented as tree: date Day may 2015

Example (1) How to structures the following expression? (a + b) * (c - 5)

Example (1) How to structures the following expression? (a + b) * (c - 5) Using symbols : * , + , and – as functors: 1. *(, ) 2. *( +(a, b) , ). 3. *(+(a, b), -(c, 5) ) * - + a b c 5

Matching - examples ▫ date(D, M, 2001) and date(D 1, may, Y 1) ▫ date(D, M, 2001) and date(D 1, M 1, 1444) ▫ date(X, Y, Z) and point(X, Y, Z)

Matching - examples • ? - date(D, M, 2001)=date(D 1, may, Y 1), date(D, M, 2001)=date(15, M, Y). To satisfy the first goal : date(D, M, 2001)=date(D 1, may, Y 1). , prolog instantiation will be: D=D 1, M = may, Y 1= 2001. After specifying the second goal, the instantiation become more specific as follow: D= D 1, D 1 = 15, M = may, Y 1= Y , Y = 2001.

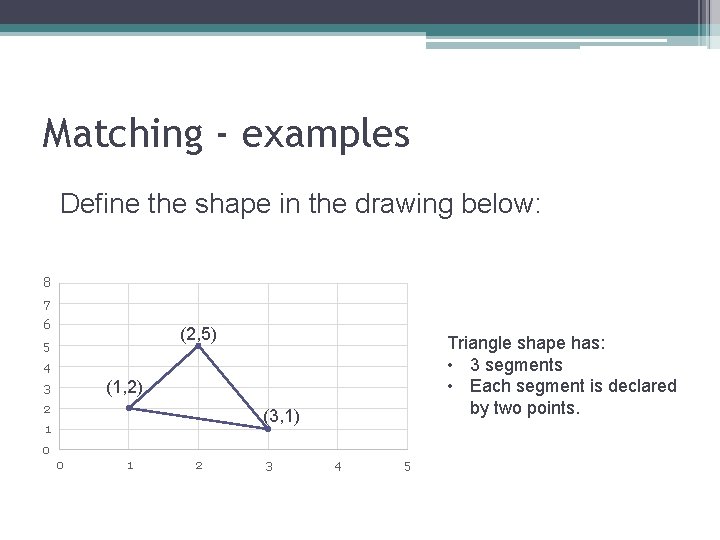
Matching - examples Define the shape in the drawing below: 8 7 6 (2, 5) 5 Triangle shape has: • 3 segments • Each segment is declared by two points. 4 (1, 2) 3 2 (3, 1) 1 0 0 1 2 3 4 5

Matching - examples 8 7 (2, 5) 6 5 4 (1, 2) 3 point(1, 2). point(2, 5). point(3, 1). (3, 1) 2 1 0 0 1 2 3 4 5 triangle(point(1, 2) , point(2, 5) , point(3, 1)). seg(point(1, 2), point(2, 5)). seg(point(2, 5), point(3, 1)). seg(point(1, 2), point(3, 1)). triangle(seg(point(1, 2), point(2, 5)), seg(point(2, 5), point(3, 1)), seg(point(1, 2), point(3, 1)

Matching - examples triangle point 1 A 2 triangle point 3 X 1 The result instantiation is: A = point(2, Y), X = point(1, 2), Z =3, B=1. point 2 Y point Z B

Matching - examples Declare vertical and horizontal relations 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 vertical (seg(point(X, _), point(X, _))). horizontal (seg(point(_, Y), point(_, Y))).

Matching – examples (cont. ) ▫ Is the segment (1, 1), (1, 4) is vertical? ▫ Are there any vertical segment that start at point(2, 3)? ▫ Is there a segment that is both vertical and horizontal?

Class exercise (1) ▫ Is the segment (1, 1), (2, Y) vertical? ▫ Is the segment (1, 1), (2, Y) horizontal

Class exercise (1) (cont. ) ▫ Is the segment (1, 1), (2, Y) vertical? ? - vertical (seg(point(1, 1), point(2, Y))). No ▫ Is the segment (1, 1), (2, Y) horizontal ? - horizontal (seg(point(1, 1), point(2, Y))). Y=1

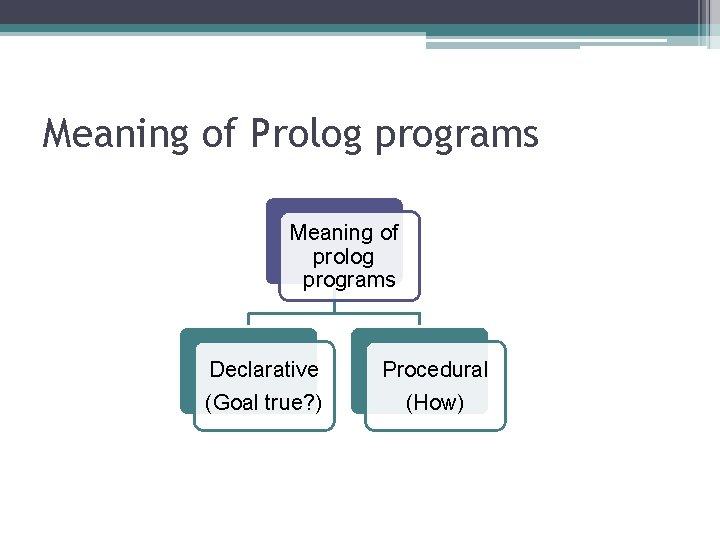
Meaning of Prolog programs Meaning of prolog programs Declarative (Goal true? ) Procedural (How)

Meaning of Prolog programs • Consider the clause: P : - Q, R. ▫ Declarative readings: �P is true if Q and R is true �From Q and R follows P ▫ Procedural readings: �To solve problem P, first solve the subproblem Q, and then the subproblem R. �To satisfy P, first satisfy Q and then R.

Meaning of Prolog programs • Consider the clause: P : - Q ; R. ▫ Same as the following two clauses together: P : - Q. P : - R. • The comma binds stronger than the semicolon. ▫ P : - Q , R ; S , T , U. is understood as: ▫ P : - ( Q , R ) ; ( S , T , U ). and means the same as the clauses: ▫ P : - Q , R. ▫ P : - S , T , U.
Class Exercise • Define the relation: Max( X , Y , Max ). So that Max is the greater of two numbers X and Y.