Chapter 2 STATICS OF PARTICLES Forces are vector

Chapter 2 STATICS OF PARTICLES Forces are vector quantities; they add according to the parallelogram law. The magnitude and direction of the resultant R of two forces P and Q can be determined either graphically or by trigonometry. R P A Q

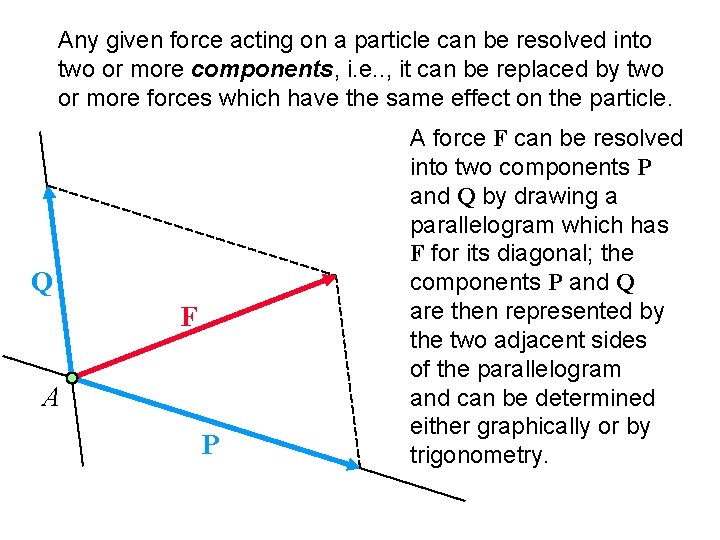
Any given force acting on a particle can be resolved into two or more components, i. e. . , it can be replaced by two or more forces which have the same effect on the particle. Q F A P A force F can be resolved into two components P and Q by drawing a parallelogram which has F for its diagonal; the components P and Q are then represented by the two adjacent sides of the parallelogram and can be determined either graphically or by trigonometry.

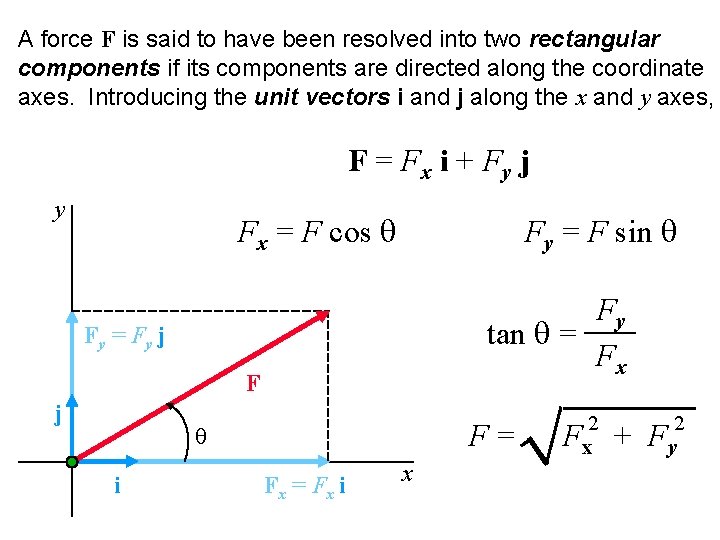
A force F is said to have been resolved into two rectangular components if its components are directed along the coordinate axes. Introducing the unit vectors i and j along the x and y axes, F = Fx i + Fy j y Fx = F cos q Fy = F sin q Fy tan q = Fx Fy = Fy j F= q i Fx = Fx i x 2 Fx + 2 Fy

When three or more coplanar forces act on a particle, the rectangular components of their resultant R can be obtained by adding algebraically the corresponding components of the given forces. Rx = S Rx Ry = S Ry The magnitude and direction of R can be determined from Ry tan q = Rx R= 2 Rx + 2 Ry

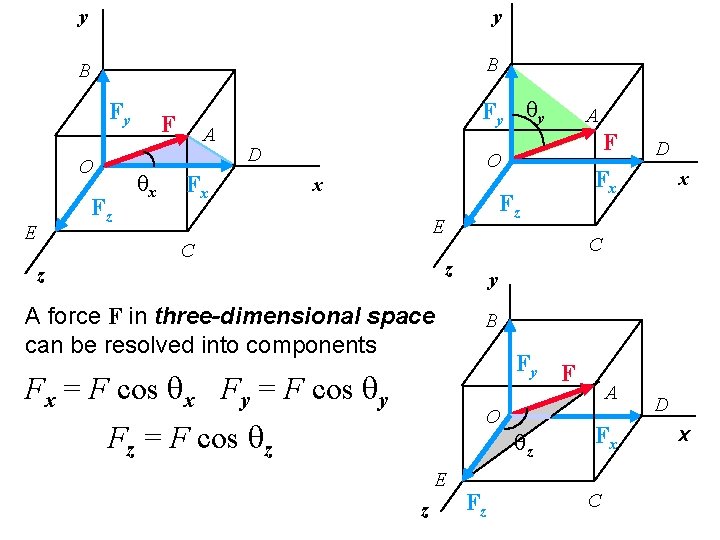
y y B B Fy O E Fz F qx A Fy qy D Fx O x Fz E C A force F in three-dimensional space can be resolved into components Fx = F cos qx Fy = F cos qy E z D Fx x y B Fy F O Fz = F cos qz F C z z A Fz qz A Fx C D x

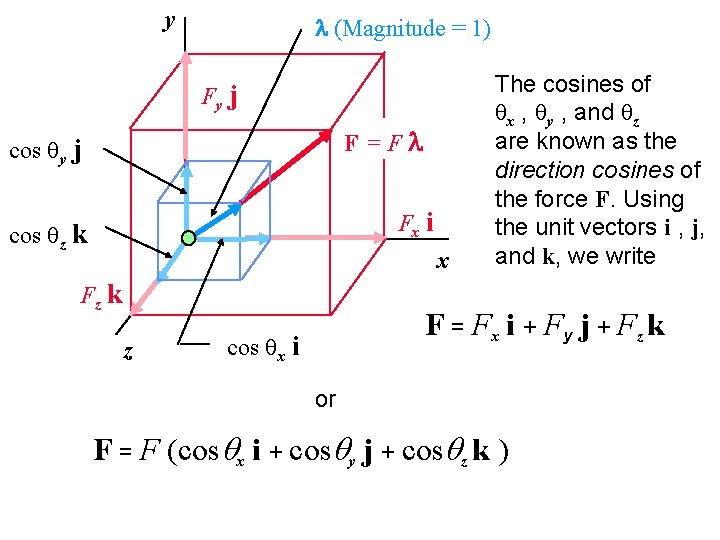
y l (Magnitude = 1) Fy j F=Fl cos qy j Fx i cos qz k x Fz k z The cosines of qx , qy , and qz are known as the direction cosines of the force F. Using the unit vectors i , j, and k, we write F = Fx i + Fy j + Fz k cos qx i or F = F (cosqx i + cosqy j + cosqz k )

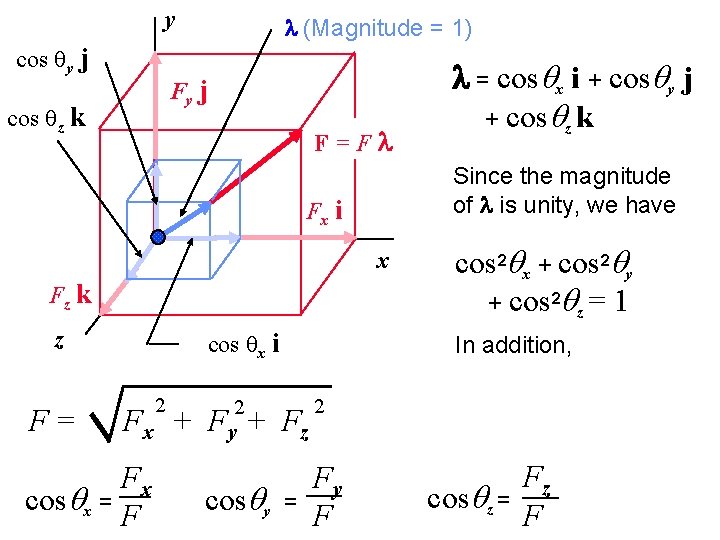
y cos qy j l (Magnitude = 1) Fy j cos qz k F=Fl Since the magnitude of l is unity, we have Fx i x Fz k z F= cos qx i 2 Fx + Fx cosqx = F 2 Fy + cosqy l = cosqx i + cosqy j + cosqz k cos 2 qx + cos 2 qy + cos 2 qz = 1 In addition, Fz = 2 Fy F cosqz = Fz F

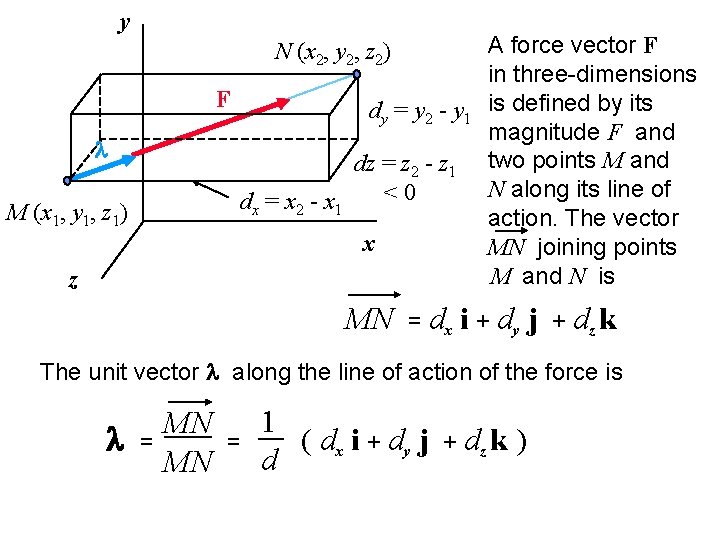
y N (x 2, y 2, z 2) F l dy = y 2 - y 1 dz = z 2 - z 1 <0 dx = x 2 - x 1 M (x 1, y 1, z 1) x z MN A force vector F in three-dimensions is defined by its magnitude F and two points M and N along its line of action. The vector MN joining points M and N is = dx i + dy j + dz k The unit vector l along the line of action of the force is l = MN MN = 1 ( dx i + dy j d + dz k )

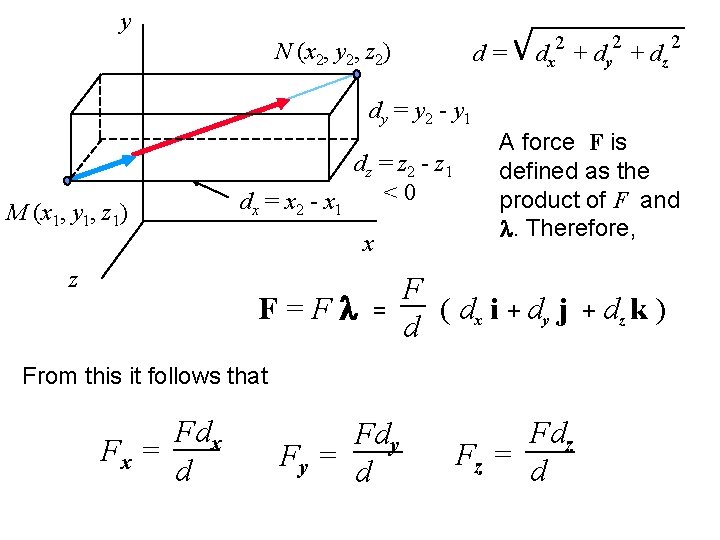
y N (x 2, y 2, z 2) d= 2 2 dx + dy + dz 2 dy = y 2 - y 1 M (x 1, y 1, z 1) dz = z 2 - z 1 <0 dx = x 2 - x 1 x z F=Fl = A force F is defined as the product of F and l. Therefore, F ( dx i + dy j d From this it follows that Fdx Fx = d Fdy Fy = d Fdz Fz = d + dz k )

When two or more forces act on a particle in threedimensions, the rectangular components of their resultant R is obtained by adding the corresponding components of the given forces. Rx = S Fx Ry = S Fy Rz = S Fz The particle is in equilibrium when the resultant of all forces acting on it is zero.

To solve a problem involving a particle in equilibrium, draw a free-body diagram showing all the forces acting on the particle. The conditions which must be satisfied for particle equilibrium are S Fx = 0 S Fy = 0 S Fz = 0 In two-dimensions , only two of these equations are needed S Fx = 0 S Fy = 0