Chapter 2 Simplex method q Geometric view x

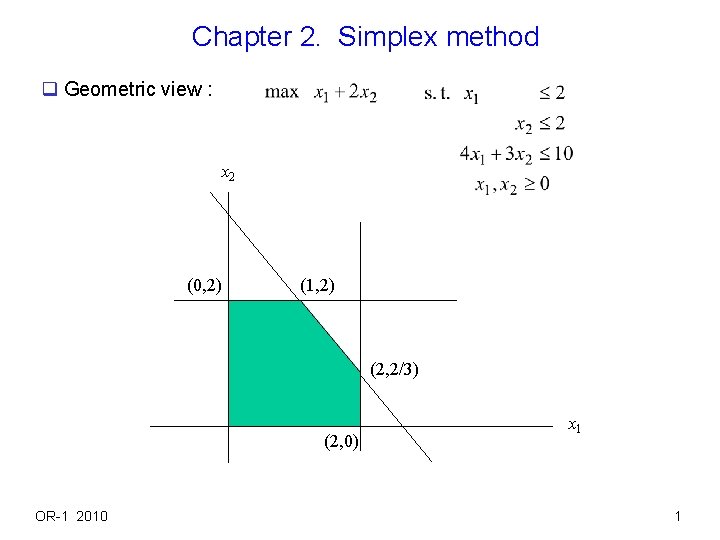
Chapter 2. Simplex method q Geometric view : x 2 (0, 2) (1, 2) (2, 2/3) (2, 0) OR-1 2010 x 1 1

q Let a Rn, b R. Geometric intuition for the solution sets of { x : a’x = 0 } { x : a’x = b } { x : a’x b } OR-1 2010 2

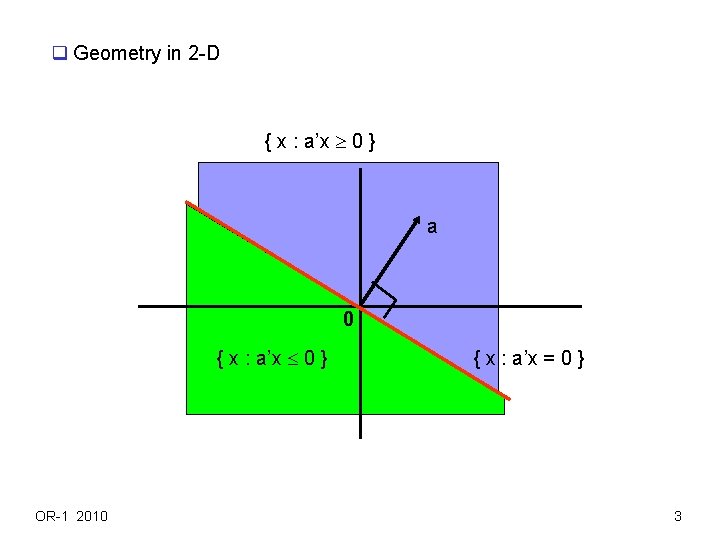
q Geometry in 2 -D { x : a’x 0 } a 0 { x : a’x 0 } OR-1 2010 { x : a’x = 0 } 3

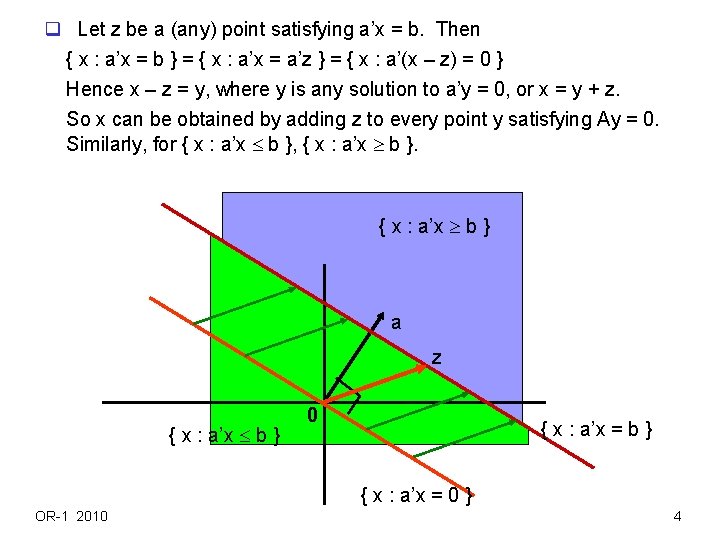
q Let z be a (any) point satisfying a’x = b. Then { x : a’x = b } = { x : a’x = a’z } = { x : a’(x – z) = 0 } Hence x – z = y, where y is any solution to a’y = 0, or x = y + z. So x can be obtained by adding z to every point y satisfying Ay = 0. Similarly, for { x : a’x b }, { x : a’x b } a z { x : a’x b } 0 { x : a’x = b } { x : a’x = 0 } OR-1 2010 4

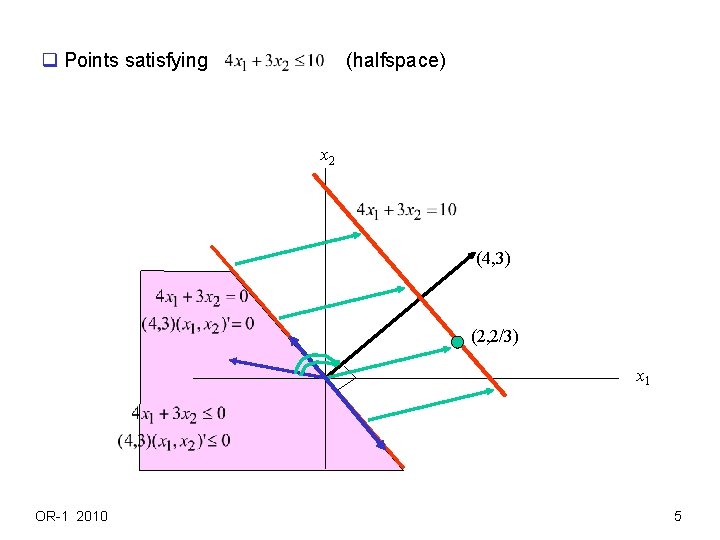
q Points satisfying (halfspace) x 2 (4, 3) (2, 2/3) x 1 OR-1 2010 5

q Def: The set of points which can be described in the form is called a polyhedron. ( Intersection of finite number of halfspaces) Hence, linear programming is the problem of optimizing (maximize, minimize) a linear function over a polyhedron. q Thm: Polyhedron Pf) HW earlier. is a convex set. q To understand the simplex method, we will consider geometric intuition and algebraic logic together throughout the lectures. OR-1 2010 6

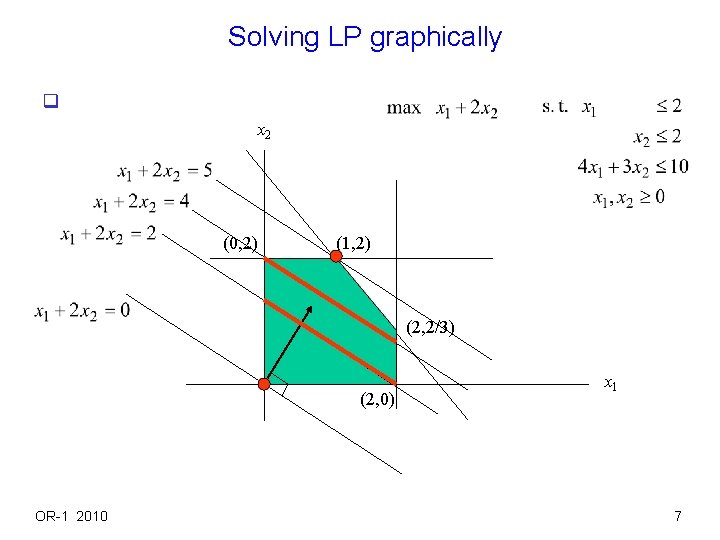
Solving LP graphically q x 2 (0, 2) (1, 2) (2, 2/3) (2, 0) OR-1 2010 x 1 7

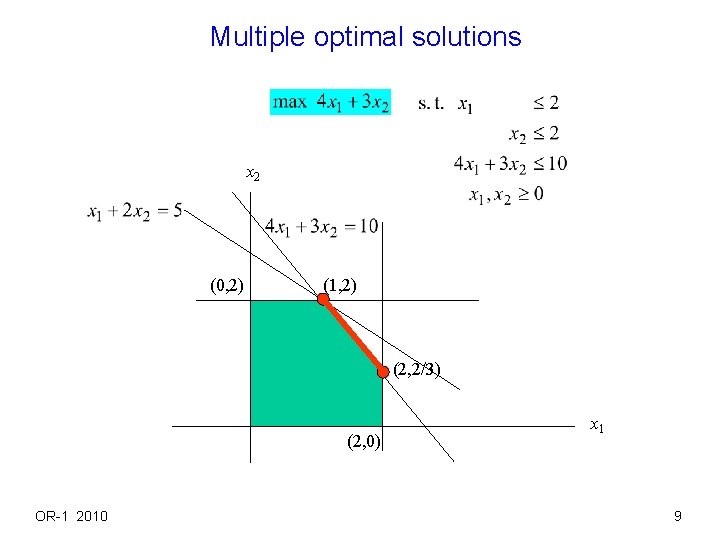
Properties of optimal solutions q Thm: If LP has a unique optimal solution, the optimal solution is an extreme point. Pf) Suppose x* is a unique optimal solution and it is not extreme point of the feasible set. Then there exist feasible points y, z x* such that x* = y +(1 - )z for some 0 < < 1. Then c’x* = c’y + (1 - )c’z. If c’x* c’y, then either c’y > c’x* or c’z > c’x*, hence contradiction to x* being optimal solution. If c’x* = c’y, y is also optimal solution. Contradiction to x* being unique optimal. � q Thm: Suppose polyhedron P has at least one extreme point. If LP over P has an optimal solution, it has an extreme point optimal solution. Pf) not given here. � OR-1 2010 8

Multiple optimal solutions x 2 (0, 2) (1, 2) (2, 2/3) (2, 0) OR-1 2010 x 1 9

Obtaining extreme point algebraically x 2 (0, 2) (1, 2) (2, 2/3) (2, 0) OR-1 2010 x 1 Extreme point (0, 2) can be iden tified by solving system of eq. x 1 = 0, x 2 = 2 Similarly, (1, 2) can be identified by 4 x 1 + 3 x 2 = 10, x 2 = 2. Note that 4 x 1 + 3 x 2 = 10, x 2 = 0 gives (5/2, 0), which is not an extreme point since it is not in the polyhedron. 10

q Suppose polyhedron is given (A: mxn), (the space is n-dimensional). Extreme point of the polyhedron can be obtained by setting n of the inequalities as equations (coefficient vectors (chosen rows of A matrix) must be linearly independent so that the system gives a unique solution. ) and obtaining the solution satisfying the equations. If the obtained point satisfies other inequalities, it is in P and it is an extreme point of the polyhedron q Above result needs rigorous proof, but we use it here without proof since the proof is quite involved and the result itself is crucial in understanding the simplex method. q From the previous theorems, we only need to consider extreme points of the polyhedron to find an optimal solution. OR-1 2010 11

q Enumeration of all extreme points? : maximum of , which is quite large. ( the number of ways to choose n inequalities (which hold at equalities) out of (m+n) inequalities. ) q Algorithm strategy : from an extreme point, move to the neighboring extreme point which gives a better (precisely speaking, not worse) solution in each iteration of the algorithm. OR-1 2010 12

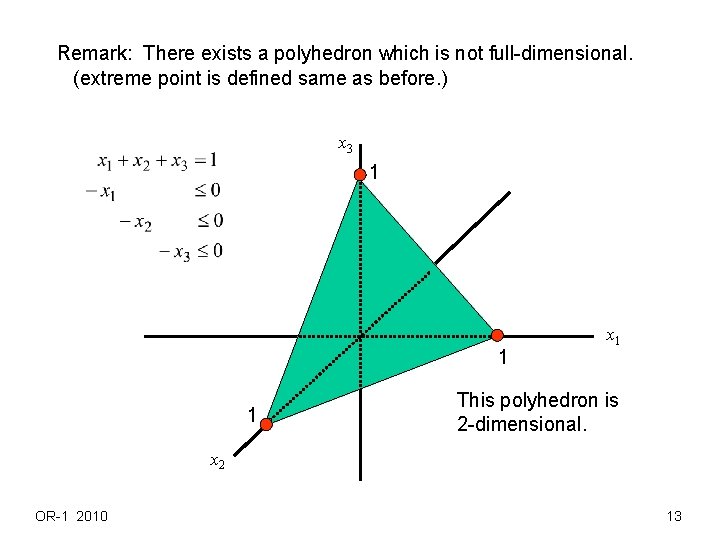
Remark: There exists a polyhedron which is not full-dimensional. (extreme point is defined same as before. ) x 3 1 1 1 x 1 This polyhedron is 2 -dimensional. x 2 OR-1 2010 13

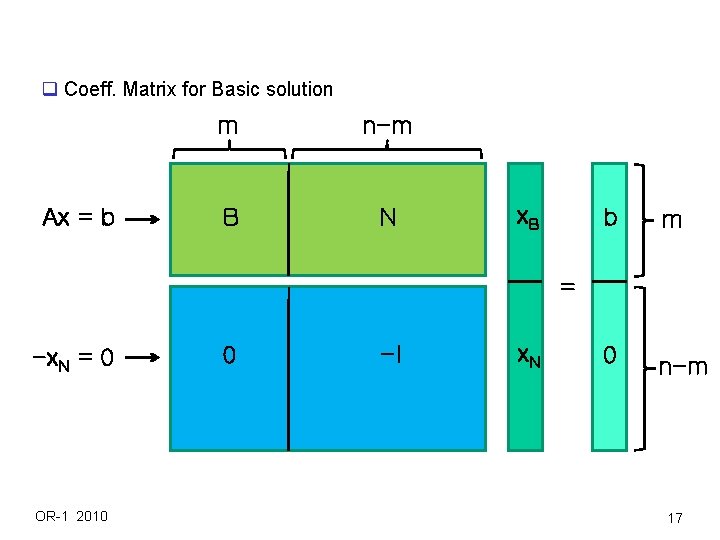
Geometric Idea of the Simplex Method q Any LP problem must be converted to a problem having only equations except the nonnegativity constraints if simplex method can be applied (details later) q Consider the LP problem max c’x, Ax = b, -x 0 A: m n, full row rank (n m) P = { x : Ax=b, -x 0 } To define an extreme point of P, we need n equations. Since we already have m equations in Ax=b, (n - m) equations must come from -x 0, which means (n - m) variables are set to 0. Let A=[B: N], where N is the submatrix corresponding to the variables set to 0. Then we solve the system Bx = b for the remaining m variables. (Note that the coefficient matrix B must be nonsingluar so that the system of equations has a unique solution. ) OR-1 2010 14

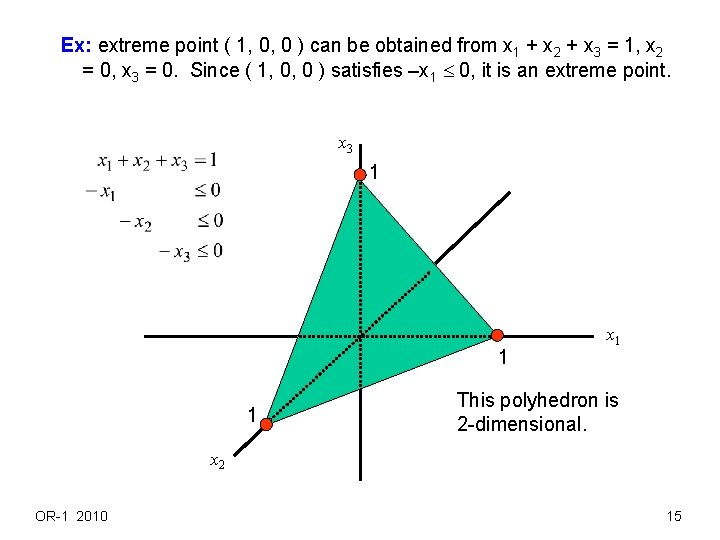
Ex: extreme point ( 1, 0, 0 ) can be obtained from x 1 + x 2 + x 3 = 1, x 2 = 0, x 3 = 0. Since ( 1, 0, 0 ) satisfies –x 1 0, it is an extreme point. x 3 1 1 1 x 1 This polyhedron is 2 -dimensional. x 2 OR-1 2010 15

(continued) Let A = [B : N] , B: m m, nonsingular, N: m (n - m), where N is the submatrix of A having columns associated with variables set to 0. Then an extreme point can be found by solving Ax = b, x. N = 0. [B : N] (x. B’: x. N’ )’ = b Bx. B + Nx. N = b, -x. N = 0. (or Bx. B = b - Nx. N , -x. N = 0. ) multiplying B-1 on both sides, we obtain B-1 Bx. B + B-1 Nx. N = B-1 b or Ix. B + B-1 Nx. N = B-1 b, -x. N = 0. ( x. B = B-1 b - B-1 Nx. N , -x. N = 0 ) Solution is x. B = B-1 b, x. N = 0 This is the basic solution we mentioned earlier. By the choice of the variables we set at 0, we obtain different basic solutions (different extreme points). x. B are called basic variables, and x. N are called nonbasic variables. q If the obtained solution satisfies nonnegativity, x. B = B-1 b 0, we have a basic and feasible solution (satisfies nonnegativity of variables). So this point is in the polyhedron P = { x : Ax=b, -x 0 } and an extreme point. ) OR-1 2010 16

q Coeff. Matrix for Basic solution Ax = b m n-m B N x. B b m 0 n-m = -x. N = 0 OR-1 2010 0 -I x. N 17

q Suppose A: n n, then |A| (determinant of A) is given as |A| = j=1 n aij Aij for any i = i=1 n aij Aij for any j, where Aij = (-1)i + j |Mij|. Mij is a (n-1)-square submatrix of A obtained by deleting i-th row and jth column of A (called minor of aij ). Aij is called the cofactor of aij. Ø Also A is nonsingular if and only if |A| 0. Ø square matrix A is nonsingular Ax = b has a unique solution. q Hence the condition that the system in the previous slide has a unique solution is equivalent to the condition that the coefficient matrix is nonsingular determinant of the coefficient matrix 0 determinant of B matrix 0 B is nonsingular. Hence we need the condition that B matrix is nonsingular when we define an extreme point, i. e. basic feasible solution. OR-1 2010 18

q Simplex method searches only basic feasible solutions, which is tantamount to searching the extreme points of the corresponding polyhedron until it finds an optimal solution. OR-1 2010 19

Simplex method (algebraic interpretation) (1) Add slack variables(여유변수) to each constraint to convert them to equations. (2) OR-1 2010 20

q q Hence we have a 1 -1 mapping which maps each feasible point in (1) to a feasible point in (2) uniquely (and conversely) and the objective values are the same for the points. So solve (2) instead of (1) and disregard the value of slack variables to obtain an optimal solution to the original problem. (Surplus variable (잉여변수) : a’x b a’x – xs = b, xs 0 ) OR-1 2010 21

q Remark: If LP includes equations, we need to convert each equation to two inequalities to express the problem in standard form as we have seen earlier. Then we may add slack or surplus variables to convert them to equations. However, this procedure will increase the number of constraints and variables. Equations in an LP can be handled directly without changing them to inequalities. Detailed method will be explained in Chap 8. General LP Problems. For the time being, we assume that we follow the standard procedure to convert equations to inequalities. OR-1 2010 22

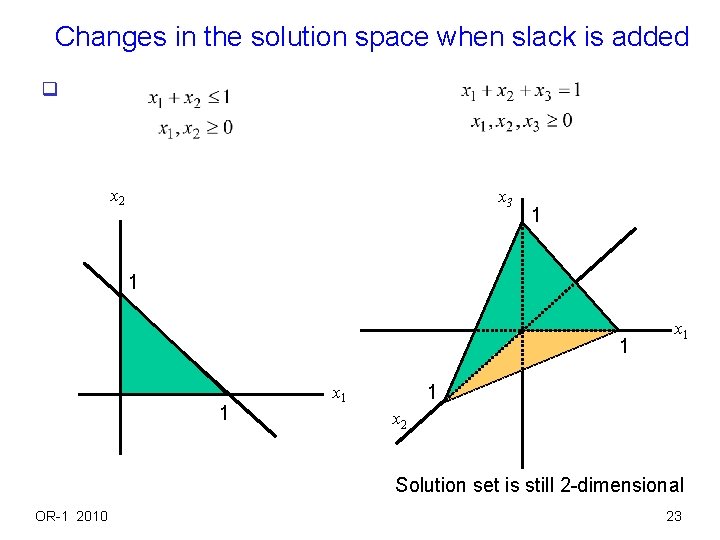
Changes in the solution space when slack is added q x 2 x 3 1 1 x 2 Solution set is still 2 -dimensional OR-1 2010 23

q. Next let Then find solution to the following system which maximizes z (tableau form) In the text, dictionary form used, i. e. each dependent variable (including z) (called basic variable) is expressed as linear combinations of indep. var. (called nonbasic variable). (Note that, unlike the text, we place the objective function in the first row. Such presentation style is used more widely and we follow that convention) OR-1 2010 24

q From previous lectures, we know that if the polyhedron P has at least one extreme point and the LP over P has a finite optimal value, the LP has an extreme point optimal solution. Also an extreme point of P for our problem is a basic feasible solution algebraically. We obtain a basic solution by setting x 1 = x 2 = x 3 = 0 and finding the values of x 4, x 5, and x 6 , which can be read directly from the dictionary. (also z values can be read. ) If all values of x 4, x 5, and x 6 are nonnegative, we obtain a basic feasible solution. q The equation for z may be regarded as part of the systems of equations, or we may think of it as a separate equation used to evaluate the objective value for the given solution. OR-1 2010 25