Chapter 2 SIGNALS AND SPECTRA Chapter Objectives Basic

Chapter 2 SIGNALS AND SPECTRA Chapter Objectives: • Basic signal properties (DC, RMS, d. Bm, and power); • Fourier transform and spectra; • Linear systems and linear distortion; • Band limited signals and sampling; • Discrete Fourier Transform; • Bandwidth of signals. Huseyin Bilgekul Eeng 360 Communication Systems I Department of Electrical and Electronic Engineering Eastern Mediterranean University Eeng 360 1

Properties of Signals & Noise Ø In communication systems, the received waveform is usually categorized into two parts: Signal: The desired part containing the information. Noise: The undesired part ØProperties of waveforms include: • DC value, • Root-mean-square (rms) value, • Normalized power, • Magnitude spectrum, • Phase spectrum, • Power spectral density, • Bandwidth • ………………. . Eeng 360 2

Physically Realizable Waveforms Ø Physically realizable waveforms are practical waveforms which can be measured in a laboratory. Ø These waveforms satisfy the following conditions • The waveform has significant nonzero values over a composite time interval that is finite. • The spectrum of the waveform has significant values over a composite frequency interval that is finite • The waveform is a continuous function of time • The waveform has a finite peak value • The waveform has only real values. That is, at any time, it cannot have a complex value a+jb, where b is nonzero. Eeng 360 3
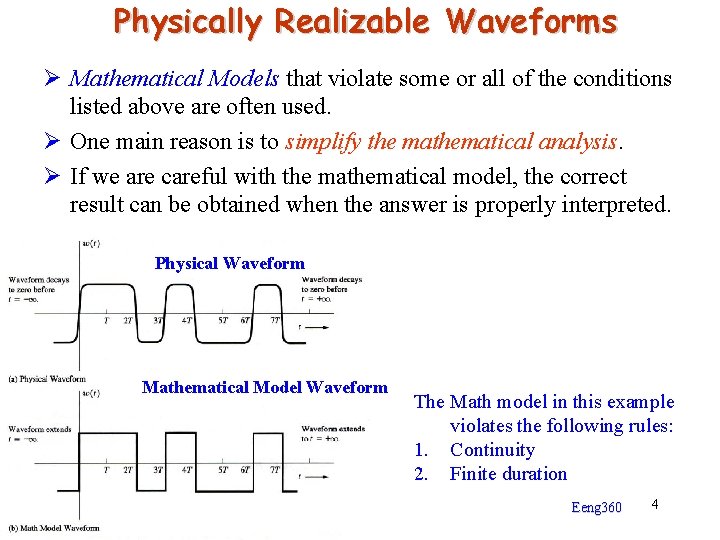
Physically Realizable Waveforms Ø Mathematical Models that violate some or all of the conditions listed above are often used. Ø One main reason is to simplify the mathematical analysis. Ø If we are careful with the mathematical model, the correct result can be obtained when the answer is properly interpreted. Physical Waveform Mathematical Model Waveform The Math model in this example violates the following rules: 1. Continuity 2. Finite duration Eeng 360 4

Time Average Operator Ø Definition: The time average operator is given by, Ø The operator is a linear operator, • the average of the sum of two quantities is the same as the sum of their averages: Eeng 360 5

Periodic Waveforms Ø Definition A waveform w(t) is periodic with period T 0 if, w(t) = w(t + T 0) for all t where T 0 is the smallest positive number that satisfies this relationship Ø A sinusoidal waveform of frequency f 0 = 1/T 0 Hertz is periodic Ø Theorem: If the waveform involved is periodic, the time average operator can be reduced to where T 0 is the period of the waveform and a is an arbitrary real constant, which may be taken to be zero. Eeng 360 6
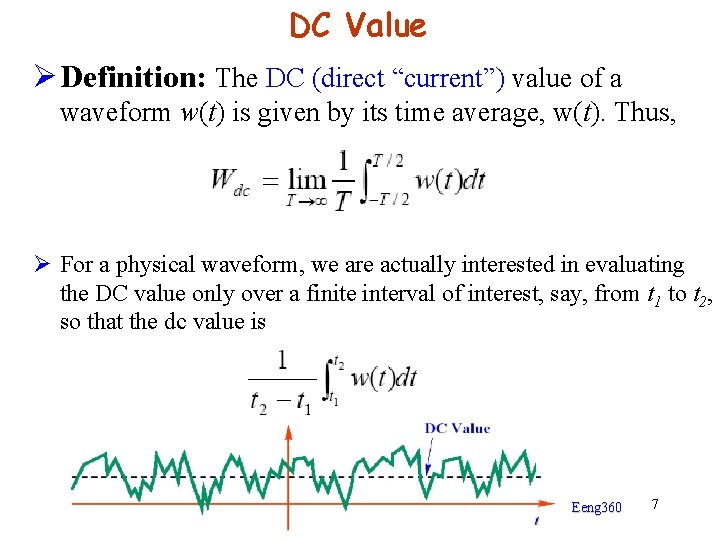
DC Value Ø Definition: The DC (direct “current”) value of a waveform w(t) is given by its time average, w(t). Thus, Ø For a physical waveform, we are actually interested in evaluating the DC value only over a finite interval of interest, say, from t 1 to t 2, so that the dc value is Eeng 360 7
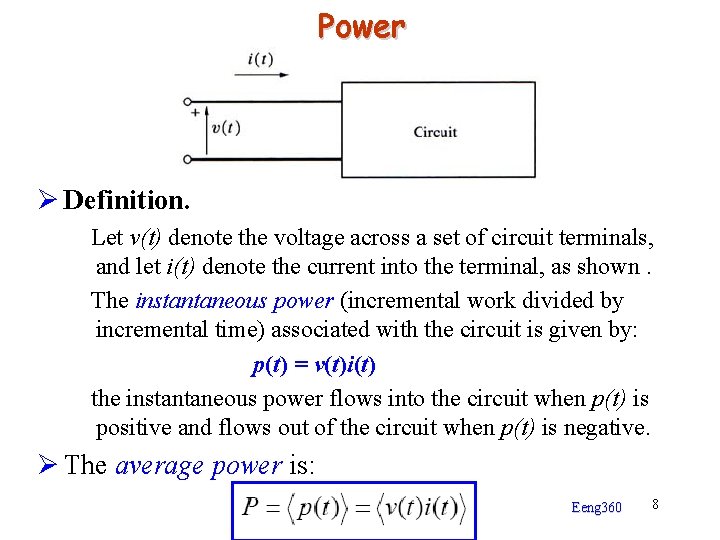
Power Ø Definition. Let v(t) denote the voltage across a set of circuit terminals, and let i(t) denote the current into the terminal, as shown. The instantaneous power (incremental work divided by incremental time) associated with the circuit is given by: p(t) = v(t)i(t) the instantaneous power flows into the circuit when p(t) is positive and flows out of the circuit when p(t) is negative. Ø The average power is: Eeng 360 8
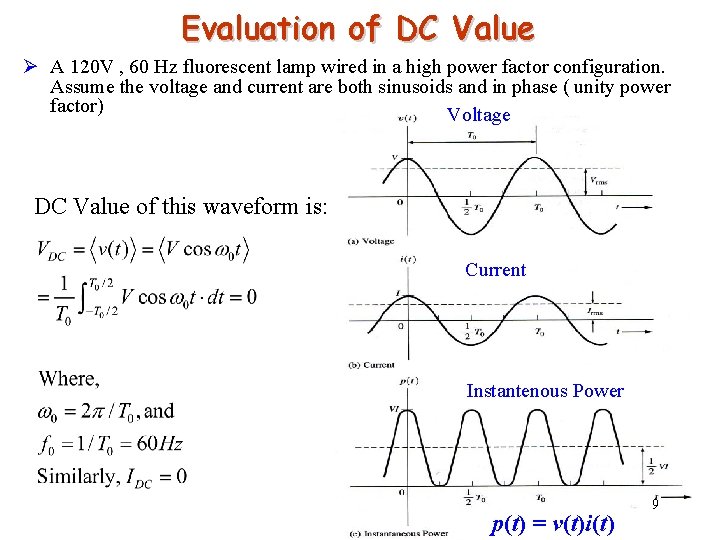
Evaluation of DC Value Ø A 120 V , 60 Hz fluorescent lamp wired in a high power factor configuration. Assume the voltage and current are both sinusoids and in phase ( unity power factor) Voltage DC Value of this waveform is: Current Instantenous Power Eeng 360 p(t) = v(t)i(t) 9
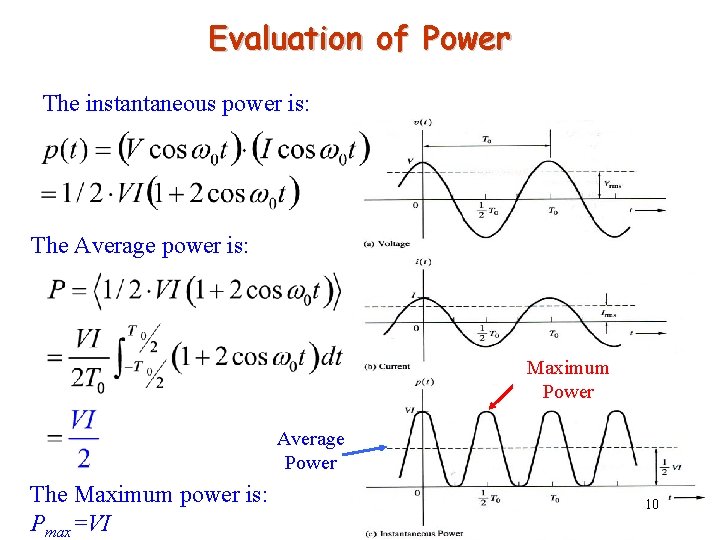
Evaluation of Power The instantaneous power is: The Average power is: Maximum Power Average Power The Maximum power is: Pmax=VI Eeng 360 10

RMS Value Ø Definition: The root-mean-square (rms) value of w(t) is: Ø Rms value of a sinusoidal: Ø Theorem: If a load is resistive (i. e. , with unity power factor), the average power is: where R is the value of the resistive load. Eeng 360 11

Normalized Power Ø In the concept of Normalized Power, R is assumed to be 1Ω, although it may be another value in the actual circuit. Ø Another way of expressing this concept is to say that the power is given on a per-ohm basis. Ø It can also be realized that the square root of the normalized power is the rms value. Definition. The average normalized power is given as follows, Where w(t) is the voltage or current waveform Eeng 360 12

Energy and Power Waveforms Ø Definition: w(t) is a power waveform if and only if the normalized average power P is finite and nonzero (0 < P < ∞). Ø Definition: The total normalized energy is Ø Definition: w(t) is an energy waveform if and only if the total normalized energy is finite and nonzero (0 < E < ∞). Eeng 360 13

Energy and Power Waveforms Ø If a waveform is classified as either one of these types, it cannot be of the other type. Ø If w(t) has finite energy, the power averaged over infinite time is zero. Ø If the power (averaged over infinite time) is finite, the energy if infinite. Ø However, mathematical functions can be found that have both infinite energy and infinite power and, consequently, cannot be classified into either of these two categories. (w(t) = e-t). Ø Physically realizable waveforms are of the energy type. – We can find a finite power for these!! Eeng 360 14

Decibel Ø A base 10 logarithmic measure of power ratios. Ø The ratio of the power level at the output of a circuit compared with that at the input is often specified by the decibel gain instead of the actual ratio. Ø Decibel measure can be defined in 3 ways • • • Decibel Gain Decibel signal-to-noise ratio Mill watt Decibel or d. Bm Ø Definition: Decibel Gain of a circuit is: Eeng 360 15

Decibel Gain Ø If resistive loads are involved, Definition of d. B may be reduced to, or Eeng 360 16

Decibel Signal-to-noise Ratio (SNR) Ø Definition. The decibel signal-to-noise ratio (S/R, SNR) is: Where, Signal Power (S) = And, Noise Power (N) = So, definition is equivalent to Eeng 360 17

Decibel with Mili watt Reference (d. Bm) Ø Definition. The decibel power level with respect to 1 m. W is: = 30 + 10 log (Actual Power Level (watts) • Here the “m” in the d. Bm denotes a milliwatt reference. • When a 1 -W reference level is used, the decibel level is denoted d. BW; • when a 1 -k. W reference level is used, the decibel level is denoted d. Bk. E. g. : If an antenna receives a signal power of 0. 3 W, what is the received power level in d. Bm? d. Bm = 30 + 10 xlog(0. 3) = 30 + 10 x(-0. 523)3 = 24. 77 d. Bm Eeng 360 18

Phasors Ø Definition: A complex number c is said to be a “phasor” if it is used to represent a sinusoidal waveform. That is, where the phasor c quantity {. }. = |c|ej c and Re{. } denotes the real part of the complex Ø The phasor can be written as: Eeng 360 19
- Slides: 19