Chapter 2 Signals and Linear Systems Text Book

Chapter 2. Signals and Linear Systems Text Book: Essentials of Communication Systems Engineering - John G. Proakis and Masoud Salehi Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 1

2. 0 Pre-requisites: 2. 0. 1 Sine & Cosine Functions n Definisions: Y y r θ O x X Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 2

2. 0 Pre-requisites: 2. 0. 1 Sine & Cosine Functions Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 3

2. 0 Pre-requisites: 2. 0. 2 Complex Numbers n Notations: Y y r θ O x X Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 4

2. 0 Pre-requisites: Exercises Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 5

2. 1 Basic Concepts: 2. 1. 1 Basic Operations on Signals n n x(t) : A signal Time shifting or delaying n y(t) : Time shifted version of x(t) : ¨ ¨ n , t 0 : Time shift When t 0 > 0, x(t) is shifted to the right : time delay When t 0 < 0, x(t) is shifted to the left : time advance Time reversal, or flipping n y(t) : Signal by replacing time t by –t : ¨ Reflected version of x(t) about t = 0 Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 6

Basic Operations on Signals n Time scaling n n Expands (stretches) or contracts (compresses) a signal along the time axis y(t) : Signal by scaling the independent variable, time t, by a factor a ¨ ¨ n If a>1, the signal y(t) is a compressed version of x(t) If 0<a<1, the signal y(t) is an expanded version of x(t) Combination of these operation n n x(-2 t) = Combination of flipping the signal then contracting it by a factor of 2 x(2 t-3) : x[2(t-1. 5)] = Contract the signal by a factor of 2 and then shifting it to the right by 1. 5 Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 7

2. 1. 2 Classification of Signals: Real and Complex Signals n Real signals n n n Takes its values in the set of real numbers x(t) R, t R Complex signals n n n Takes its values in the set of complex numbers x(t) C , t R In communications ¨ ¨ ¨ Used to model signals Convey amplitude and phase information Represented by two real signals § Real and imaginary parts § Absolute value (or modulus or magnitude) and phase Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 8

Representation of Complex signals – Example 2. 1. 3 n The signal : ¨ n n Complex signals n From Euler’s relation : ¨ Its real part : ¨ Its imaginary part : n Absolute value of x(t) : n Its phase : Figure 2. 8 Representation of complex signals Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 9

Periodic and Nonperiodic Signals n Periodic signals n The signal x(t) is periodic if and if only (iff) there exists a T 0 >0 such that ¨ T 0 : period of the signals (positive real number) the minimum value satisfying the condion n A signal that does not satisfy the conditions of periodicity is called non-periodic Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 10

Even and Odd Signals n Even ¨ n Odd A signal x(t) is said to be an even signals if Signals ¨ n In Signals A signal x(t) is said to be an odd signals if general, any signal x(t) can be written as the sum of its even and odd part as Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 11

Hermitian Symmetry for Complex Signals n Hermitian symmetry n n n Another form of symmetry for complex signals A complex signal x(t) is called Hermitian if its real part is even and its imaginary part is odd Its magnitude is even and its phase is odd Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 12

Energy-Type and Power-Type Signals n Energy of the signal n n For any signal x(t), the energy of the signal is defined by Power of the signal n For any signal x(t), the power of the signal is defined by n For real signal, is replaced by n A signal is an energy-type signal if and only if Ex is finite n A signal is an power-type signal if and only if Px satisfies Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 13

Example 2. 1. 9 n The energy of n Therefore, this signal is an energy-type signal. Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 14

Example 2. 1. 10 n The energy content of n n Therefore, this signal is not an energy-type signal However, the power of this signal is n Hence, x(t) is a power-type signal and its power is Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 15

Example 2. 1. 11 n For any periodic signal with period T 0, the energy is n n Therefore, periodic signals are not typically energy type The power of any periodic signal is n This means that the power content of a periodic signal is equal to the average power in one period Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 16

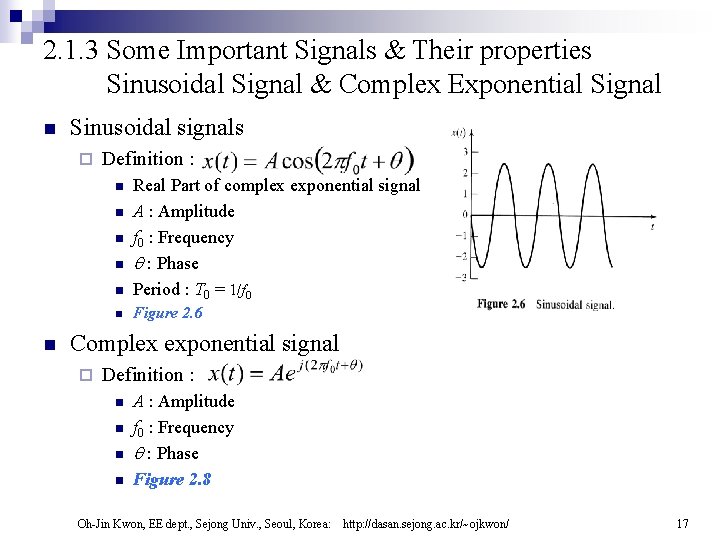
2. 1. 3 Some Important Signals & Their properties Sinusoidal Signal & Complex Exponential Signal n Sinusoidal signals ¨ Definition : n Real Part of complex exponential signal A : Amplitude f 0 : Frequency : Phase Period : T 0 = 1/f 0 n Figure 2. 6 n n n Complex exponential signal ¨ Definition : n n A : Amplitude f 0 : Frequency : Phase Figure 2. 8 Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 17

Unit Step, Rectangular & Triangular Signal n Unit step signal ¨ Definition n n Rectangular pulse, Square signal, П signal ¨ Definition n n The unit step multiplied by any signal produces a “causal version” of the signal Note that for positive a, we have Figure 2. 9 Figure 2. 13 Triangular Signal ¨ Definition n Figure 2. 15 Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 18

Example 2. 1. 12, 13, 14 n Plot the signal Figure 2. 12 . n Represent x(t) in Figure 2. 14 using rectangular pulses. n Plot the signal . Figure 2. 16 Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 19

Convolution of Two Signals n Definition n Example: p 35 n Example: p 39, property 10 Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 20

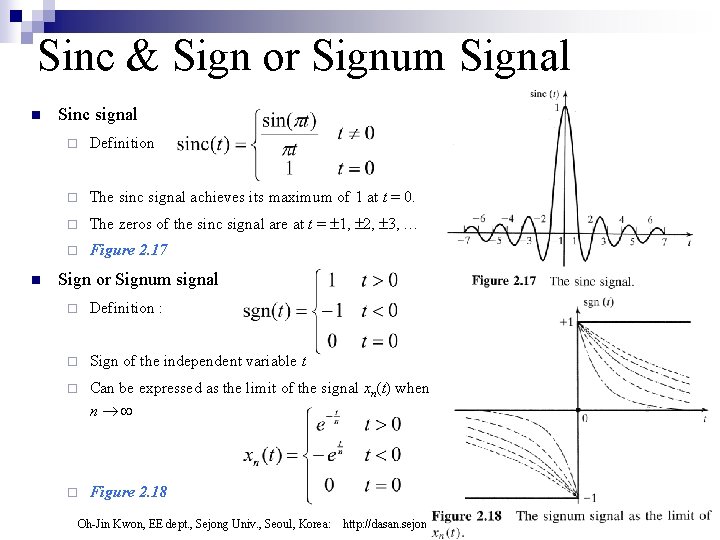
Sinc & Sign or Signum Signal n n Sinc signal ¨ Definition ¨ The sinc signal achieves its maximum of 1 at t = 0. ¨ The zeros of the sinc signal are at t = 1, 2, 3, ¨ Figure 2. 17 Sign or Signum signal ¨ Definition : ¨ Sign of the independent variable t ¨ Can be expressed as the limit of the signal xn(t) when n ¨ Figure 2. 18 Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 21 21

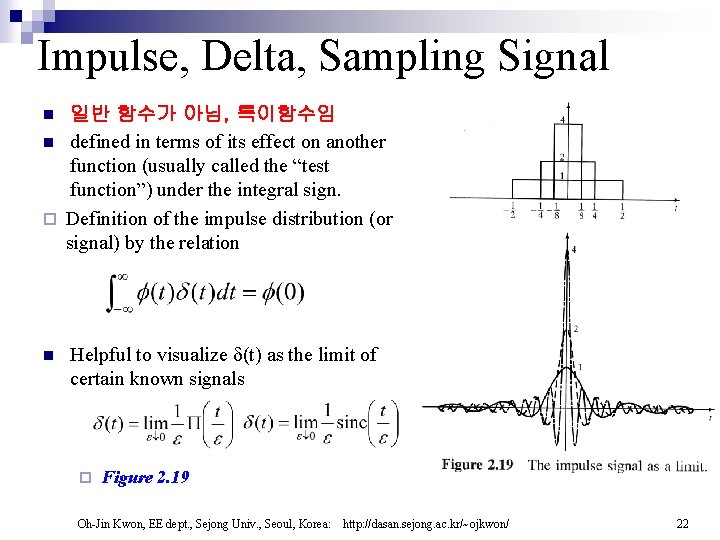
Impulse, Delta, Sampling Signal 일반 함수가 아님, 특이함수임 n defined in terms of its effect on another function (usually called the “test function”) under the integral sign. ¨ Definition of the impulse distribution (or signal) by the relation n n Helpful to visualize (t) as the limit of certain known signals ¨ Figure 2. 19 Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 22

Impulse Signal – Properties n Figure 2. 20 : Schematic representation of the impulse signal 1. (t) = 0 for all t 0 and (0) = 2. 3. x(t) (t-t 0) = x(t 0) (t-t 0) For any (t) continuous at t 0, → 다른 책에서는 (t) 의 정의식임, Sampling Signal 4. For any (t) continuous at t 0, 5. For all a 0, Let all a = -1, Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: , even signal http: //dasan. sejong. ac. kr/~ojkwon/ 23

Impulse Signal – Properties 6. The result of the convolution of any signal with the impulse signal is the signal it self : 7. The unit step signal is the integral of the impulse signal, and the impulse signal is the generalized derivative of the unit step signal Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 24

Impulse Signal – Properties 8. 9. Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 25

Impulse Signal – Exercises a) b) c) Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 26

2. 1. 4 Classification of Systems n System n n An interconnection of various elements or devices that behave as a whole. Communication point of view ¨ n Communication engineer’s point of view ¨ n A entity that is excited by an input signal and , as a result of this excitation, produces an output signal A law that assigns output signals to various input signals Its output must be uniquely defined for ant legitimate input § § § n x(t) : Input y(t) : Output : Operation performed by the system Characteristics 1. 2. The operation that describes the system : Use the operator to denote the operation The set of legitimate input signals : Use the operator H Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 27

Linear and Nonlinear Systems n Linear systems n Systems for which the superposition property is satisfied n The system response to a linear combination of the inputs is the combination of the response to the corresponding inputs ¨ A system is linear if and only if, for any two input signals x 1(t) and x 2(t) and for any two scalars and , we have ¨ A system that does not satisfy this relationship is called nonlinear ¨ Linearity : Additive + homogeneous ¨ Output of a linear system ¨ n Decompose the input into a linear combination of some fundamental signals n Linear combination of the corresponding outputs L : Operation of linear systems Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 28

Time-Invariant and Time-Varying Systems n Time-invariant system n A system is called time invariant if its input-output relationship does not change with time n A delayed version of an input results in a delayed version of the output n A system is time-invariant if and only if, for all x(t) and all values of t 0, its response to x(t-t 0) is y(t-t 0) , y(t) is the response of the system to x(t) n Linear time-invariant systems ¨ The response of these systems to inputs can be derived simply by finding the convolution of the input and the impulse response of the system Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 29

Example 2. 1. 19 -22 n Differentiating & integrating systems: → Linear & Time Invariant → RLC circuits: LTI n Time delaying system: → Linear & Time Invariant n : Nonlinear & Time Invariant n : Linear & Time Variant Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 30

Analysis of LTI Systems in the Time Domain n Impulse response n n The impulse response h(t) of a system is the response of the system to a unit impulse input (t) The convolution integral: Output y(t) of an LTI system to any input signal x(t) n Pf) Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 31

Example 2. 1. 25 n n n Let a linear time-invariant system have the impulse response h(t) Assume this system has a complex exponential signal as input, The response to the input ¨ The response of an LTI system to the complex exponential with frequency f 0 is a complex exponential with the same frequency n n n ¨ Amplitude of the response : Multiplying the amplitude of the input by Phase response : Adding to the input phase : A function of the impulse response and the input frequency Complex exponential n n n Eigenfunctions of the class of linear time-invariant systems Eigenfunctions of a system : Set of inputs for which the output is a scaling of the input Simple to find the response of LTI system to the class of complex exponential signals Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 32

HW & QZ #1 n n n n n Textbook Problems from p 105 2. 1. 1, 2. 1. 3, 2. 1. 4, 2. 1. 6, 2. 1. 9 2. 5. 1, 2. 5. 2 2. 6. 2, 2. 6. 4, 2. 6. 6 2. 7. 1, 2. 7. 2, 2. 7. 3, 2. 7. 4 2. 9. 4 2. 13. 9, 2. 13. 12, 2. 13. 15 2. 16. 1, 2. 16. 3, 2. 16. 5, 2. 16. 7, 2. 16. 9 2. 24. 1, 2. 24. 3, 2. 24. 5, 2. 24. 7, 2. 24. 9 2. 34. 1, 2. 34. 4, 2. 34. 6 Oh-Jin Kwon, EE dept. , Sejong Univ. , Seoul, Korea: http: //dasan. sejong. ac. kr/~ojkwon/ 33