Chapter 2 Section 3 Arithmetic Operations on Matrices

Chapter 2 Section 3 Arithmetic Operations on Matrices

Matrices • Rectangular array of numbers • Often described by the size (the number of rows and the number of columns). The matrix 1 2 3 4 0 8 9 6 7 6 is a 4 x 3 matrix. Four rows and 3 columns

Different Types of Matrices • See pages 74 – 75 for the definitions of the following matrices: Row Matrix Column Matrix Square Matrix

When Two Matrices are Equal Two matrices, A and B, are equal when: 1. They both are the same size AND 2. When ALL the corresponding entries are the equal.

Addition and Subtraction of Matrices • To add or subtract two matrices together, the two matrices must be exactly the same size. When they are the same size, then add (or subtract) corresponding entries. • See the examples at the top of page 76. • If the sizes of the two matrices are not the same, then their sum (or difference) is undefined.

Multiplication of Matrices • A little more complicated than addition and subtraction. • In order to multiply matrix A to matrix B (i. e. A·B) • REQUIREMENT: The number of columns in the first matrix (A) must equal the number or rows in the second matrix (B). This is referred to as the inner dimensions being equal.

Inner Dimensions Matrices: Dimensions: A m x n · B = r x c C m x c Must be equal Size of resulting matrix 1. If the inner dimensions are not the same, then the product of the two matrices is said to be undefined. 2. If the inner dimensions are the same, then the size of the resulting matrix is the number of rows from the first matrix and the number of columns from the second matrix

Example 3(a) (page 80) Calculate the product, if defined. 3 – 1 2 0 1 5 1 0 5 – 4 2 – 1 = Undefined Answer: The product is undefined, since the number of columns in the first matrix (2) is not equal to the number of row in the second matrix (3).

Example 3(b) (page 80) Calculate the product, if defined. 3 – 1 5 4 2 0 1 5 – 2 3 3 · 5 + (– 1)·(– 2) = 2 · 5 + 0 · (– 2) 1 · 5 + 5 · (– 2) Answer: = 17 10 – 5 9 8 19 3 · 4 + (– 1) · 3 2· 4+0· 3 1· 4+5· 3

Example 5 (page 79) Calculate the product using the finger method. 1 5 3 2 1 0 = 1 · 1 + 5 · 1 3· 1+2· 1 1· 2+5· 0 3· 2+2· 0 Intermediate matrix that is not shown in textbook Answer: = 6 5 2 6

Exercise 21 (page 85) Calculate the product by hand. 3 1 0 2 Answer: 1 3 4 5 = 3 · 1 + 1 · 3 0· 1+2· 3 = 6 6 17 10 3· 4+1· 5 0· 4+2· 5

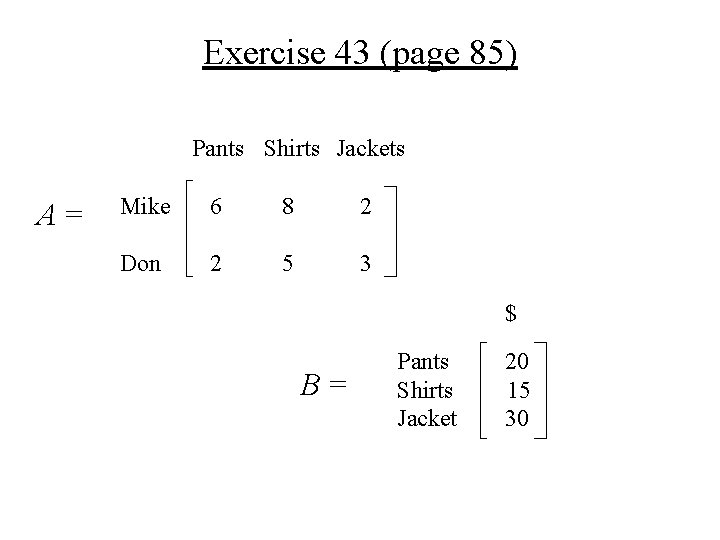
Exercise 43 (page 85) Pants Shirts Jackets A= Mike 6 8 2 Don 2 5 3 $ B= Pants Shirts Jacket 20 15 30

Exercise 43 (a) Calculate AB. Solution: AB = 6 8 2 2 5 3 20 15 30 = 6 · 20 + 8 · 15 + 2 · 30 2 · 20 + 5 · 15 + 3 · 30 = 340 265

Exercise 43 (b) • Interpret the entries in AB AB = 340 265

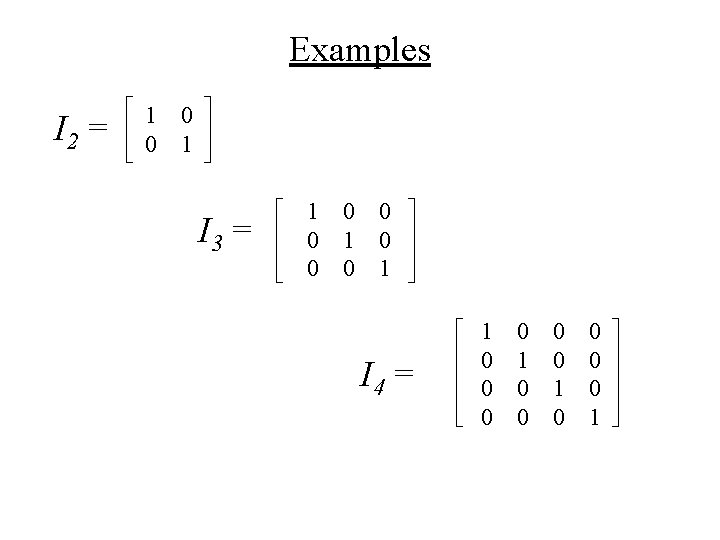
Identity Matrix ( I n ) • The identity matrix is to matrix multiplication as 1 is to multiplication of numbers. • A·I = A • I·A = A • The identity matrix – Is always a square matrix – Has 1’s on the diagonal (from top left corner to bottom right corner) and 0’s everywhere else.

Examples I 2 = 1 0 0 1 I 3 = 1 0 0 0 1 I 4 = 1 0 0 0 0 1

Matrix Equation Form • A system of equations like: – 2 x + 4 y = 2 – 3 x + 7 y = 7 can be rewritten as the matrix equation: – 2 – 3 A 4 7 · x y = 2 7 X = B

Matrix Equation Form (continued) • Where: – A is the matrix of coefficients – X is the matrix of variables – B is the matrix of constants

Exercise 33 (page 85) • Give the system of linear equations that is equivalent to the matrix equation: 1 4 7 2 5 8 3 6 9 x y z = 10 11 12

Exercise 33 (solution) • Using the finger method of multiplication: 1 x + 2 y + 3 z 4 x + 5 y + 6 z 7 x + 8 y + 9 z = x + 2 y + 3 z = 10 4 x + 5 y + 6 z = 11 7 x + 8 y + 9 z = 12 10 11 12

Exercise 37 (page 85) • Write the system of linear equations in matrix equation form (i. e. Change it to the form of A X = B): x – 2 y + 3 z = 5 y+ z=6 z=2

Exercise 37 (solution) A 1 0 0 – 2 1 0 · 3 1 1 X = x y z = B 5 6 2