Chapter 2 Section 2 1 Conditional Statements WarmUp

Chapter 2 Section 2. 1 Conditional Statements

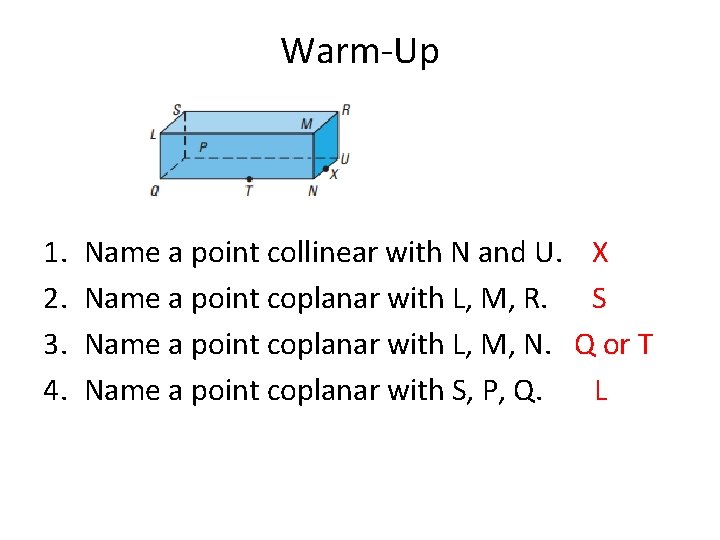
Warm-Up 1. 2. 3. 4. Name a point collinear with N and U. Name a point coplanar with L, M, R. Name a point coplanar with L, M, N. Name a point coplanar with S, P, Q. X S Q or T L

Conditional Statement • Type of logical statement • 2 parts – Hypothesis/Conclusion • Usually written in “if-then” form • If George goes to the market, then he will buy milk. Hypothesis Conclusion If the hypothesis is true then the conclusion must be true

Rewrite each conditional statement in if-then form 1. It is time for dinner if it is 6 pm. • If it is 6 pm, then it is time for dinner 2. There are 12 eggs if the carton is full • If the egg carton is full, then there are 12 eggs. 3. A number is divisible by 6 if it is divisible by 2 and 3. • If a number is divisible by 2 and 3, then it is divisible by 6 4. An obtuse angle is an agle that measures more than 90 and less than 180. • If an angle is obtuse then it measures more than 90 and less than 180. 5. All students taking geometry have math during an even numbered block • If you are taking geometry, then you have math during an even numbered block.

Counter Example • Used to prove a conditional statement is false • Must show an instance where the hypothesis is true and the conclusion is false. – Ex. If x 2 = 9 then x = 3 – Counter Ex. (-3)2 = 9, but – 3, 3 • Only need one counter example to prove something is not always true.

Decide whether the statement is true or false. If it is false, give a counter example 6. The equation 4 x – 3 = 12 + 2 x has exactly one solution • True 7. If x 2 = 36 then x = 18 or x = -18 • False: (6)2 = 36 and 6 18 or 6 -18 8. Thanksgiving is celebrated on a Thursday • True 9. If you’ve visited Springfield, then you’ve been to Illinois. • False: If you’ve visited Springfield, then you’ve been to Massachusetts (Springfield MA. ) 10. Two lines intersect in at most one point. • True

New statements formed from a conditional • Converse: Switch the hypothesis and conclusion – – Conditional: If you see lightning, then you hear thunder Converse: If you hear thunder, then you see lightning 11. If you like hockey, then you go to the hockey game • If you go to the hockey game, then you like hockey 12. If x is odd, then 3 x is odd • If 3 x is odd, then x is odd 13. If m P = 90, then P is a right angle • If P is a right angle, then m P = 90

New statements formed from a conditional • • Inverse: When you negate the hypothesis and conclusion of a conditional Negate: To write the negative of a statement – – Conditional: If you see lightning, then you hear thunder Inverse: If you do not see lightning, then you do not hear thunder 11. If you like hockey, then you go to the hockey game • If you don’t like hockey, then you don’t go to the hockey game 12. If x is odd, then 3 x is odd • If x is not odd, then 3 x is not odd 13. If m P = 90, then P is a right angle • If m P 90, then P is not a right angle

New statements formed from a conditional • Contrapositive: When you switch and negate the hypothesis and conclusion of a conditional – – Conditional: If you see lightning, then you hear thunder Contrapositive: If you do not hear thunder, then you do not see lightning 11. If you like hockey, then you go to the hockey game • If you don’t go to the hockey game, then you don’t like hockey 12. If x is odd, then 3 x is odd • If 3 x is not odd, then x is not odd 13. If m P = 90, then P is a right angle • If P is not a right angle, then m P 90

Equivalent Statements • When two statements are both true, they are called equivalent statements Original Inverse Contrapositive If m A = 30, then A is acute If m A 30, then A is not acute If A is acute, then m A = 30 If A is not acute, then m A 30

Point, Line, and Plane Postulates 5. Through any two points there exists exactly one line 6. A line contains at least two points 7. If two lines intersect, then their intersection is exactly one point (14) 8. Through any three noncollinear points there exists exactly one plane

Point, Line, and Plane Postulates 9. A plane contains at least three noncollinear points 10. If two points lie in a plane, then the line containing them lies in the same plane (15) 11. If two planes intersect the, then their intersection is a line. (16)

Use the diagram to state the postulate that verifies the statement 17. The points E, F, and H lie in a plane • Postulate #8: Through any three noncollinear points there exists one plane. 18. The points E and F lie on a line • Postulate #5: Through any two points there exists exactly one line

Use the diagram to state the postulate that verifies the statement 19. The planes Q and R intersect in a line • Postulate #11 If two planes intersect the, then their intersection is a line. 20. The points E and F lie in plane R. Therefore, line m lies in plane R • Postulate #10: If two points lie in a plane, then the line containing them lies in the same plane