Chapter 2 Relational Model Yonsei University 1 st

Chapter 2 Relational Model Yonsei University 1 st Semester, 2015 Sanghyun Park

Outline ± ± Structure of relational databases Relational algebra

Structure of Relational Databases ± Formally, given sets D 1, D 2, …, Dn, a relation r is a subset of D 1 x D 2 x … Dn. Thus a relation is a set of n-tuples (a 1, a 2, …, an) where each ai Di Order of tuples is irrelevant (tuples may be stored in an arbitrary order)

Relation Schema ± Each attribute of a relation has a name ± The set of allowed values for each attribute is called the domain of the attribute ± When A 1, A 2, …, An are attributes, R = (A 1, A 2, …, An) is a relation schema; e. g. Instructor-schema = (ID, name, dept_name, salary) ± r(R) is a relation on the relation schema R; e. g. instructor(Instructor-schema)

Keys ± Let R = (A 1, A 2, …, An) be a relation schema and K R ± K is a superkey of R if values for K are sufficient to identify a unique tuple of each possible relation r(R) ± K is a candidate key if K is minimal ± K is a primary key if it is a candidate key and it is chosen by the database designer as the principal means of identifying tuples within a relation

Query Languages ± ± Language with which user requests information from the database Categories of languages ® Procedural ® Non-procedural ± “Pure” languages ® Relational algebra ® Tuple relational calculus ® Domain relational calculus ± Pure languages form underlying basis of query languages that people use

Relational Algebra ± Procedural language ± Six basic operators ® Select ® Project ® Union ® Set difference ® Cartesian product ® Rename ± The operators take one or more relations as inputs and give a new relation as a result

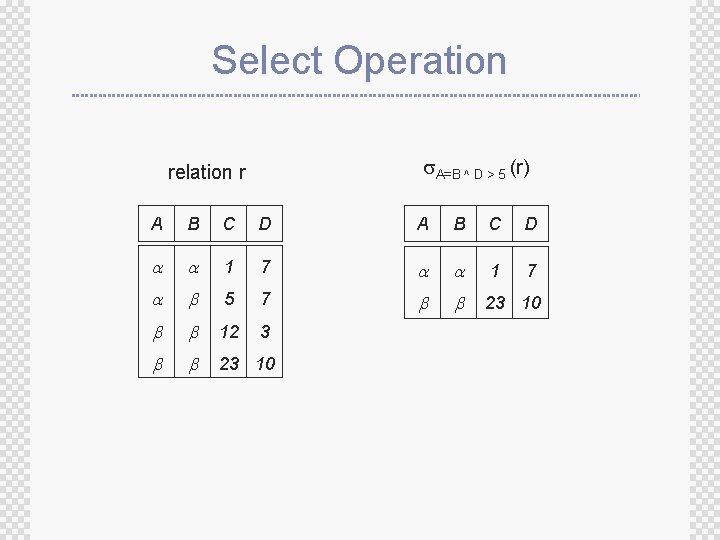
Select Operation A=B ^ D > 5 (r) relation r A B C D 1 7 5 7 23 10 12 3 23 10

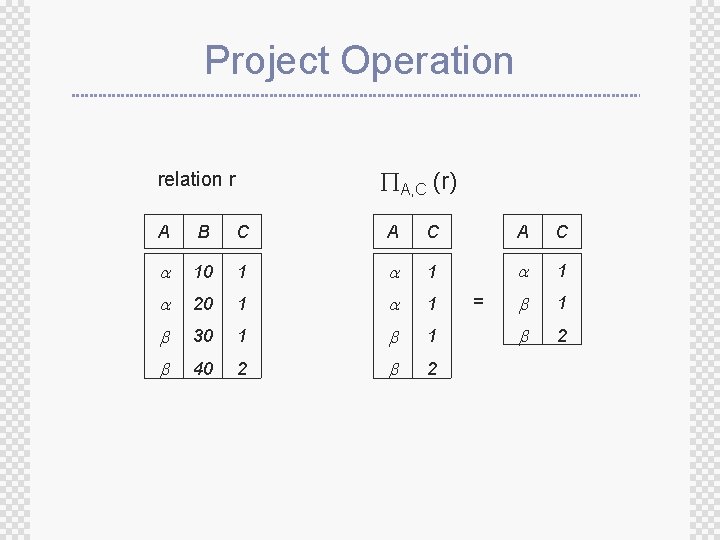
Project Operation A, C (r) relation r A B C A C 10 1 1 1 20 1 1 1 30 1 1 2 40 2 2 =

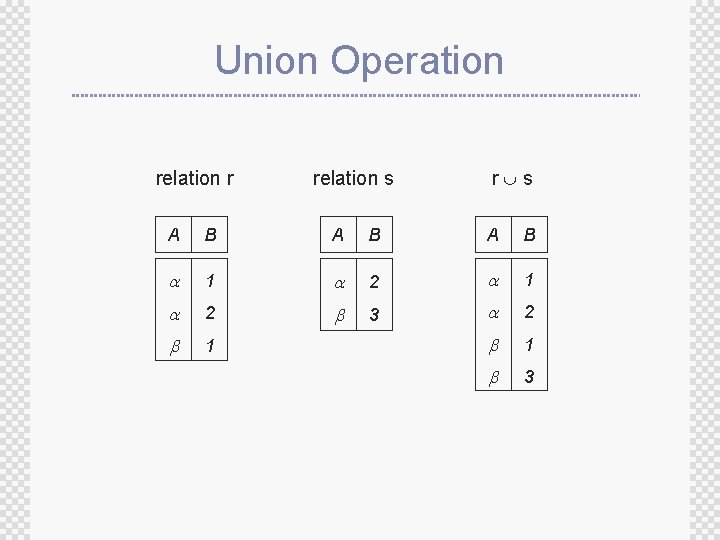
Union Operation relation r relation s r s A B A B 1 2 3 2 1 1 3

Set Difference Operation relation r relation s r-s A B A B 1 2 3 1 1

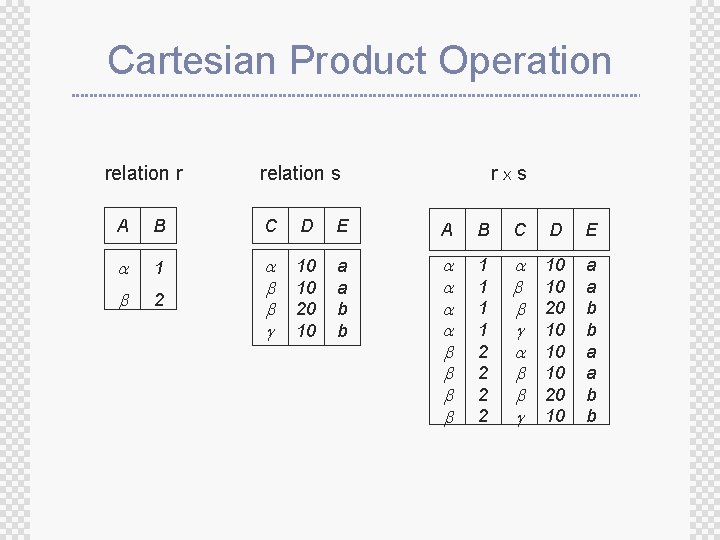
Cartesian Product Operation relation r relation s rxs A B C D E 1 2 10 10 20 10 a a b b 1 1 2 2 10 10 20 10 a a b b

Rename Operation ± Allows us to name the results of relational-algebra expressions ± Allows us to refer to a relation by more than one name ± x(E) returns the expression E under the name X ± If a relational-algebra expression E has arity n, then x(A 1, A 2, …, An) (E) returns the result of expression E under the name X, and with the attributes renamed to A 1, A 2, …, An

Additional Operations ± We define additional operations that do not add any power to the relational algebra, but that simplify common queries ± Set intersection: Natural join: Division: Assignment: ± ± ± r s r s temp 1 R-S(r)

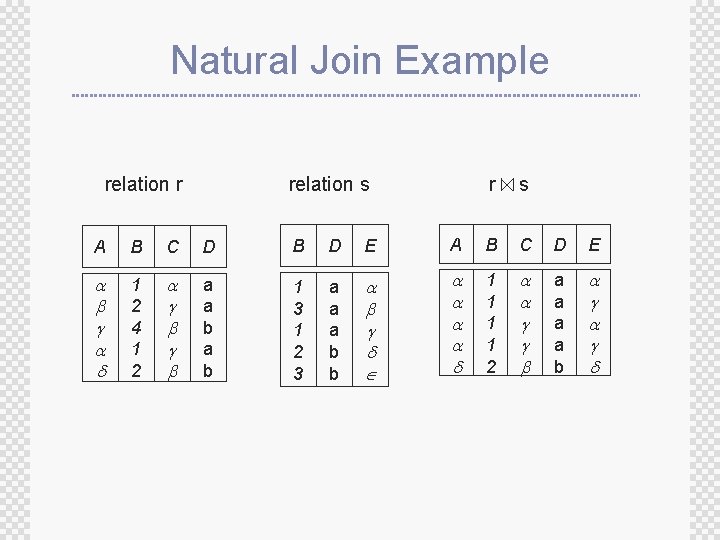
Natural Join ± Let r and s be relations on schemas R and S respectively ± Then, r s is a relation on schema R S obtained as follows: ® Consider each pair of tuples tr from r and ts from s ® If tr and ts have the same value on each of the attributes in R S, add a tuple t to the result, where t has the same value as tr on r, and t has the same value as ts on s

Natural Join Example relation r relation s r s A B C D B D E A B C D E 1 2 4 1 2 a a b 1 3 1 2 3 a a a b b 1 1 2 a a b

Outer Join ± An extension of the join operation that avoids loss of information ± Computes the join and then adds tuples from one relation that do not match tuples in the other relation to the result of the join ± Uses null values ± Left outer join, right outer join, full outer join