Chapter 2 Random Variable their Distribution Illustration Definition

Chapter 2 Random Variable & their Distribution

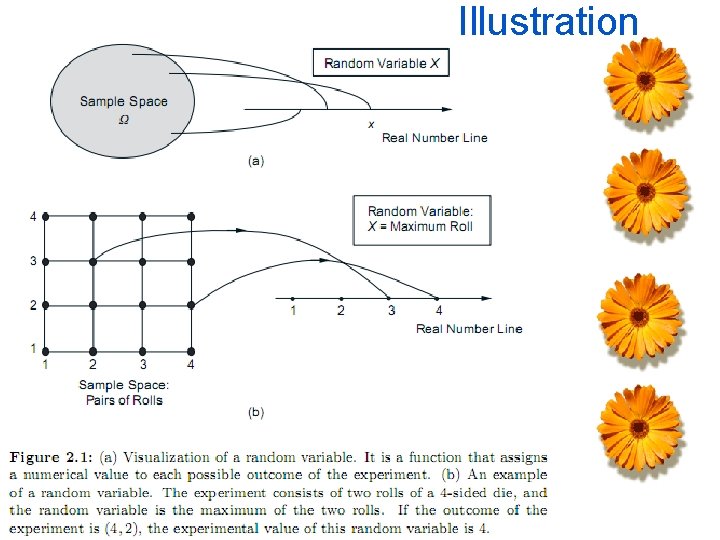
Illustration

Definition R. V say X is a function defined over a sample space S, that associates a real number, X(e)=x, whith each possible outcome e in S Look at example above!

Other Example v. An experiments involving a sequence of 5 tosses of a coin, the number of Heads in the sequence is a random variable v. Two rolls of a die, v. r : The sum of the two rolls The number of sixes in the two rolls The second roll raised to fifth power

Main Concepts Related to RV • A RV is a real valued function of the outcome of the experiment • A function of R. V defines another R. V • A R. V can be conditioned on an event or on another R. V • There is a notion of independence of a R. V from an event or from another R. V

Definition • let us consider functions which take values in the real numbers. • In the coin tossing example, our function might count the number of heads. Call this function R. We can look at the set • If we have chosen the set of events to contain all subsets of , then this set is an event, and we can ask for the probability of {R=6} • The precise relation is that if the model is ( , F, Pr) and R: (- , ) then for every interval I, {R I}: ={w : R(w) I} F

Definition : Function which satisfied Are called (real valued) R. V

Example 1 R is a R. V since for every interval I the set R I is a subset of , and all subsets of are in F

Example 2 R is not a R. V since R=2={2} is not in F

Discrete R. V si discrete if its range is finite or at most countably infinite Definition : If the set of all possible values of a R. V X is a countable set, then X called a discrete R. V f(x)=P[X=x], called the discrete probability density function (discrete pdf)

Definition

Example 1

Example 2 • The experiment consist of two independent tosses of a fair coin, let X be the number of heads obtained, then the pdf of X is :

Example 3 If Then find c!

EXERCISE

Cummulative Density Function Definition

Theorem A function F(x) is a CDF for some R. V X if and only if it satisfies the following properties :

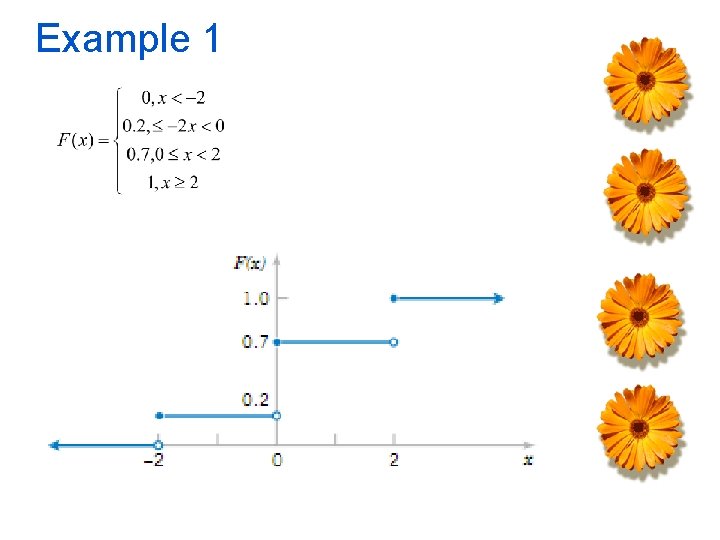
Example 1

Example 2 Suppose that a days production of 850 manufactured parts contains 50 parts that don’t conform to customer requirements. Two parts are selected at random, without replacement, from the batch. Let the random variable X equal the number of nonconforming parts in the sample. What the cdf of X?

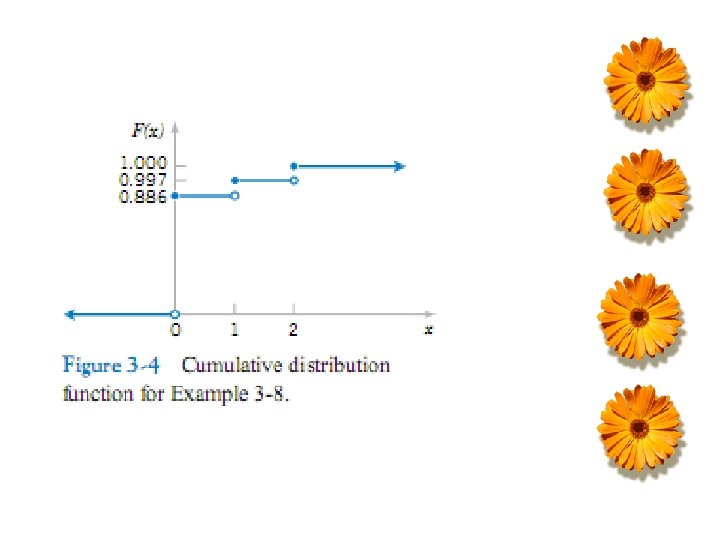
Exercise