Chapter 2 Radiation 1 Radioactivity 2 Radiation interaction































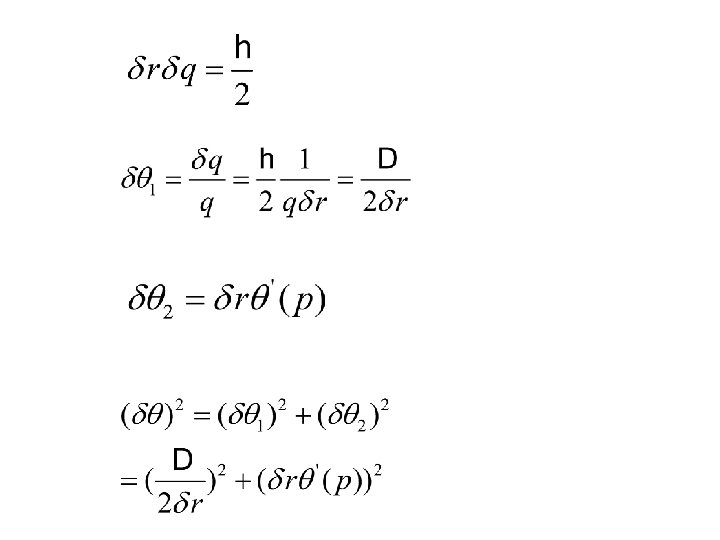
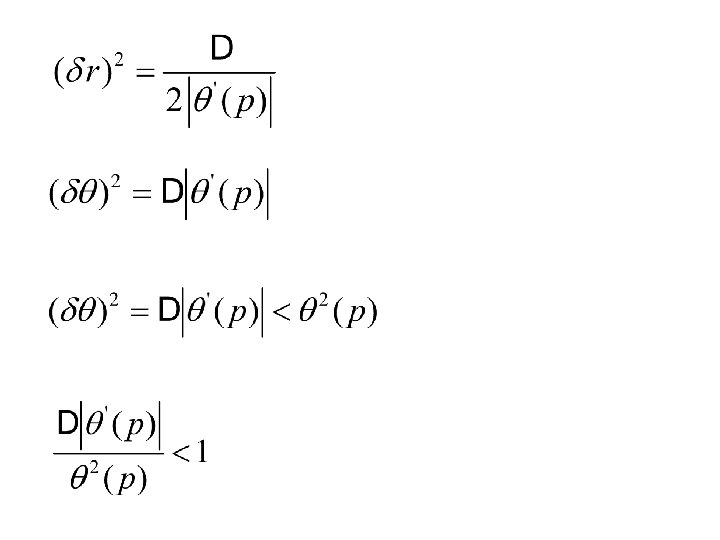
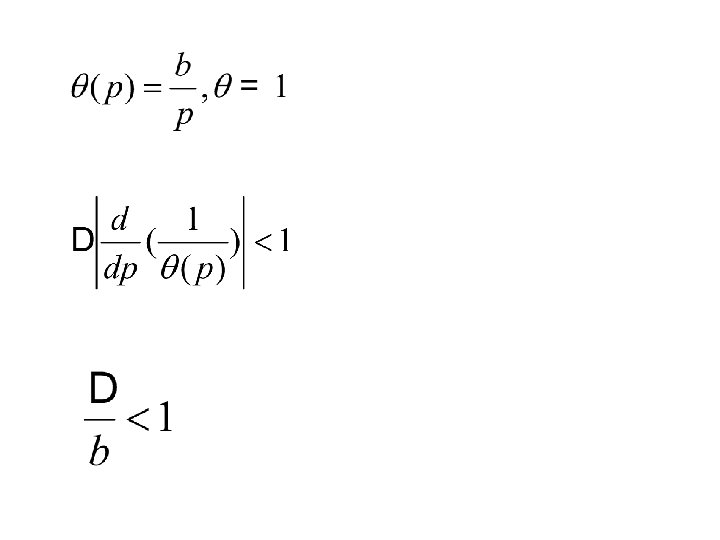


- Slides: 60

Chapter 2. Radiation 1. Radioactivity 2. Radiation interaction with Matter 3. Radiation Doses and hazard Assessment

2. 1 Radioactivity 1) 2) 3) 4) 5) 6) Overview Types of Radioactive Decay Energetics of Radioactive Decay Characteristics of Radioactive Decay Dynamics Naturally Occurring Radionuclides

2. 2 Radiation interaction with Matter 1) 2) 3) 4) overview Photon Interactions Neutron Interactions Interaction of Heavy Charged Particles with Matter 5) Scattering of Electrons in a Medium

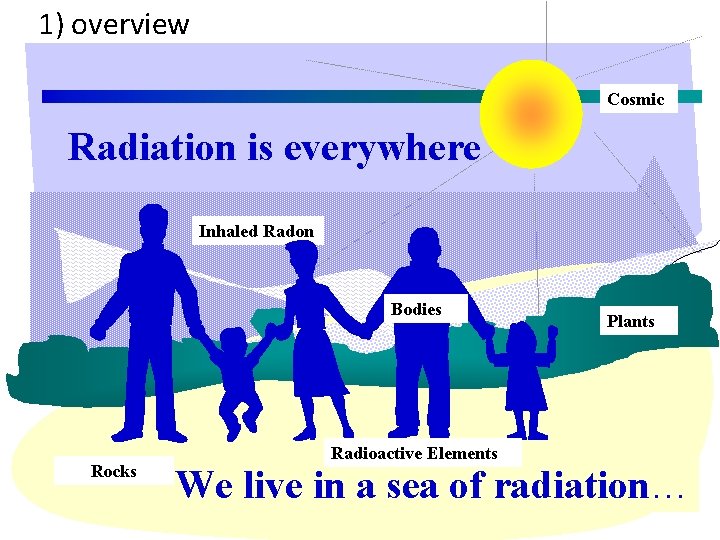
1) overview Cosmic Radiation is everywhere Inhaled Radon Bodies Rocks Radioactive Elements Plants We live in a sea of radiation…

Discovery of Ionization by Radiation X-rays and radioactivity discharged a charged electroscope. Curie and Rutherford attributed the discharge to the ionization of air by these rays. An electroscope consists of two gold leaves suspended from a metallic conductor in a glass jar

Ionization Energy of Gases The minimum energy High energy particles and required to remove an photons that ionise atoms and outer electron from atoms molecules along their tracks in a or molecules is called medium are called ionizing ionization potential. radiation Ionizing radiation also remove electrons in atomic inner shell, and He + 25 e. V He+ + ethe average energy per He+ + 54 e. V He 2+ + eion pair is considered ionization energy Ionization energy (IE e. V) per ion pair of some substances Material crystal Average IE 35 Air Xe He NH 3 22 43 39 2. 9 Ge-

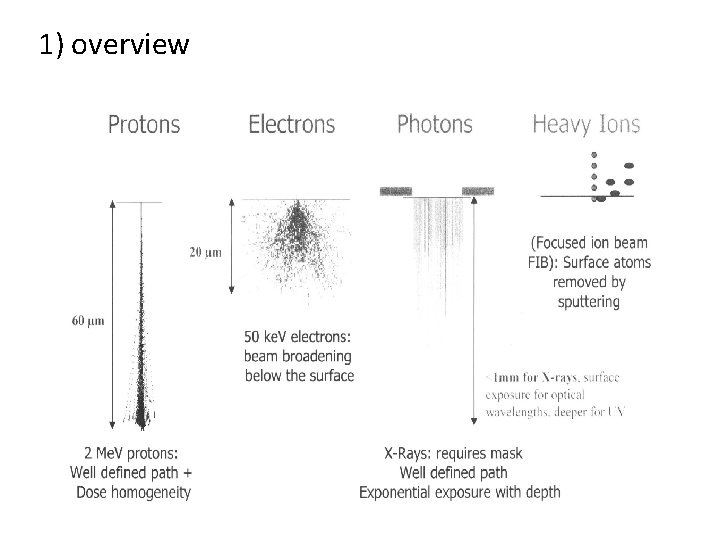
1) overview

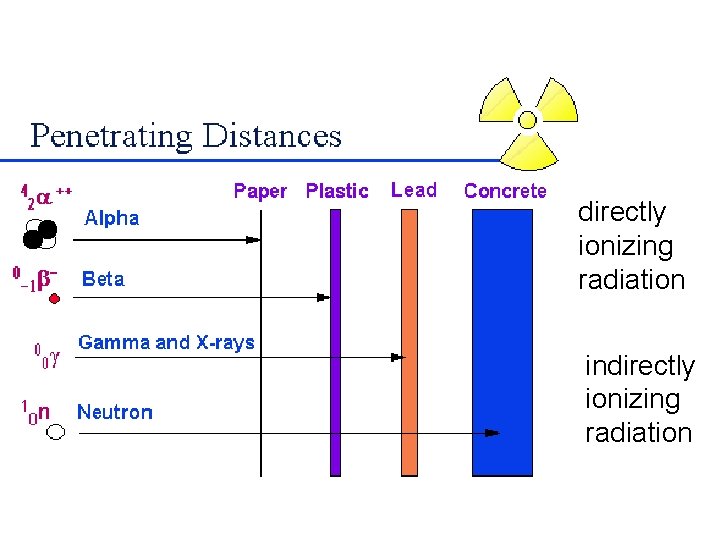
directly ionizing radiation indirectly ionizing radiation

2. 2 Radiation interaction with Matter 1) 2) 3) 4) overview Photon Interactions Neutron Interactions Interaction of Heavy Charged Particles with Matter 5) Scattering of Electrons in a Medium

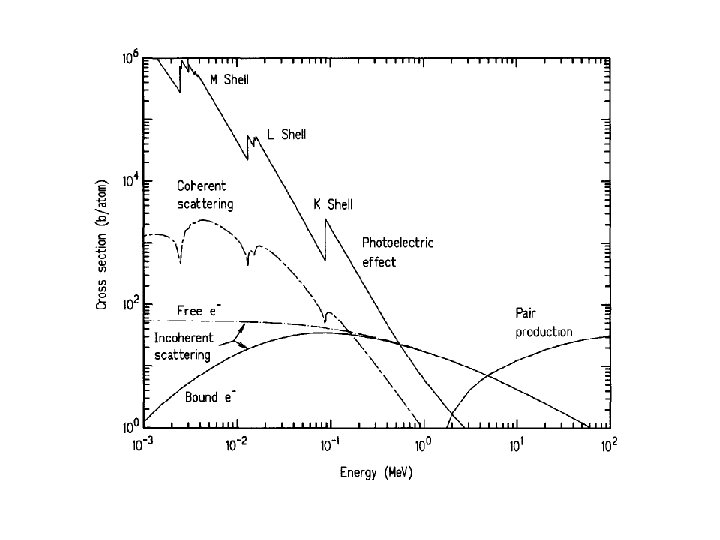
Interaction of Photons with Matter Photon Energies Visible red light 1. 5 e. V visible blue light 3. 0 e. V UV e. V X-rays ke. V few e. V-hundreds Interactions of gamma rays with matter: photoelectric effect 1 to 60 Gamma rays ke. V - some Me. V Compton effect Pair productions

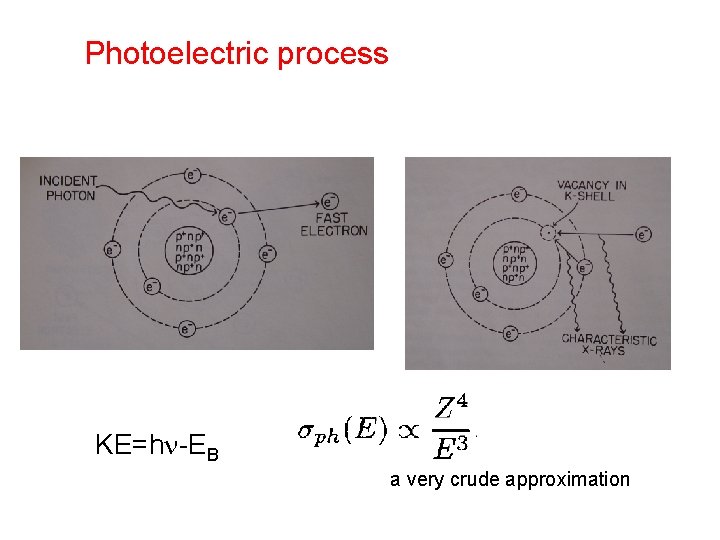
Photoelectric process KE=h -EB a very crude approximation

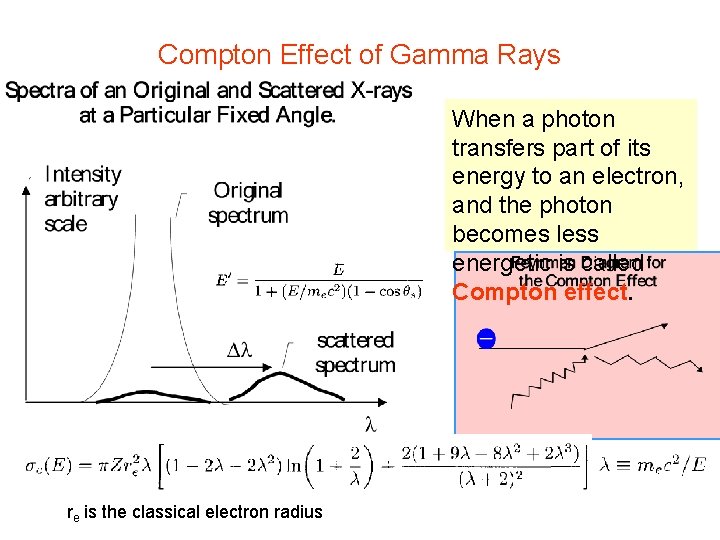
Compton Effect of Gamma Rays When a photon transfers part of its energy to an electron, and the photon becomes less energetic is called Compton effect. re is the classical electron radius

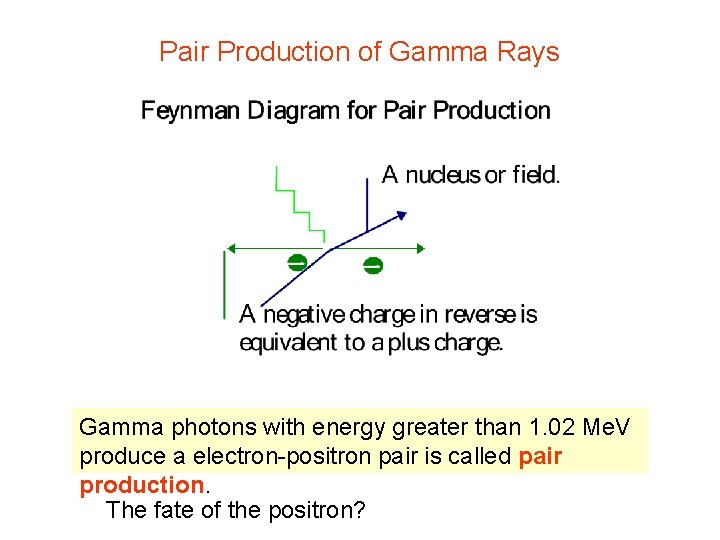
Pair Production of Gamma Rays Gamma photons with energy greater than 1. 02 Me. V produce a electron-positron pair is called pair production. The fate of the positron?

Gamma-ray Three Modes of Interaction with Matter Photoelectric effect pair production Compton scattering


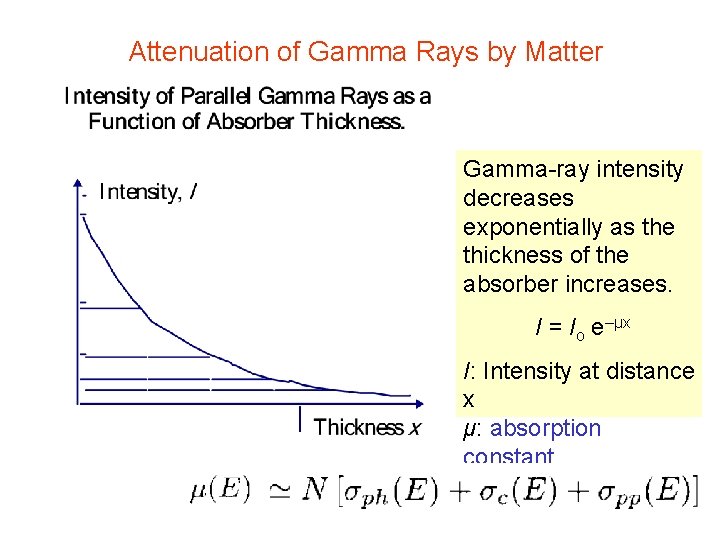
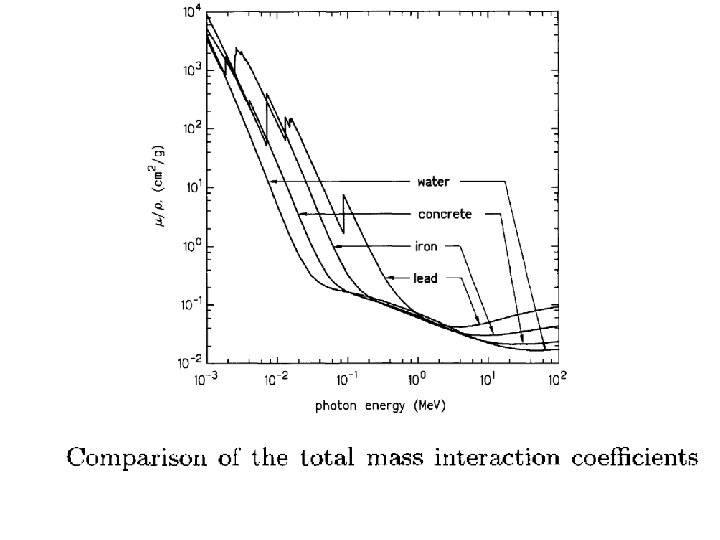
Attenuation of Gamma Rays by Matter Gamma-ray intensity decreases exponentially as the thickness of the absorber increases. I = Io e–μx I: Intensity at distance x μ: absorption constant x: thickness


Average Travel Distance Before An Interaction the interaction probability P(x) that a particle interacts somewhere along a path of length x is The probability th that a particle does not interact while traveling a distance x p(x)dx be the probability that a particle interacts for the first time between x and x + dx.

the average distance: the average distance such a particle travels before it interacts. mean-free-path length Half-Thickness: the thickness of a medium required for half of the incident radiation to undergo an interaction

What is the thickness of a water shield and of a lead shield needed to reduce a normally incident beam of 1 Me. V photons to one-tenth of the incident intensity? For water μx(1 Me. V) = 0. 07066 cm-1 and for lead μx(1 Me. V) = 0. 7721 cm-1 for water x 1/10 = 32. 59 cm, for lead x 1/10 = 2. 98 cm x 1/2 = 0. 898 cm x 1/100 = 5. 96 cm

2. 2 Radiation interaction with Matter 1) 2) 3) 4) overview Photon Interactions Neutron Interactions Interaction of Heavy Charged Particles with Matter 5) Scattering of Electrons in a Medium

Absorption of neutrons Elastic scattering • neutron collides with proton (e. g. hydrogen nucleus) and shares its kinetic energy • dominant process with fast neutrons of energy < 6 Me. V in tissue

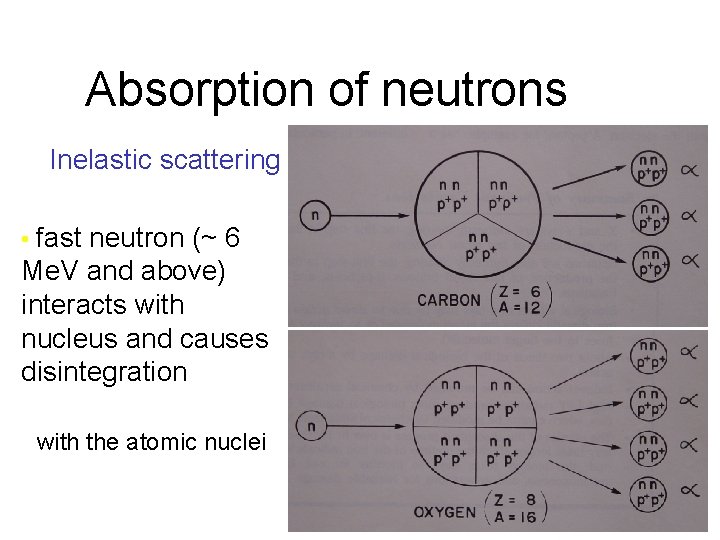
Absorption of neutrons Inelastic scattering • fast neutron (~ 6 Me. V and above) interacts with nucleus and causes disintegration with the atomic nuclei

Neutrons lose very little energy per collision when they collide with heavy nuclei. Nuclei of hydrogen and neutrons have approximately the same mass. In collisions with hydrogen nuclei, neutrons can transfer almost all their kinetic energy to the hydrogen nuclei. Thus, hydrogen‑containing compounds such as H 2 O, paraffin wax, and hydrocarbons (oil and grease) slow down neutrons rapidly.

Thermal Neutrons Cross Sections Uranium for Fission Fuel in Nuclear Reactor 113 Cd c /b 19, 820 f /b t 1/2/y 233 U 235 U 238 U 46 98 2. 7 530 580 2. 7× 10 -6 1. 6× 105 7× 108 4. 5× 109

Thermal Neutrons Cross Sections Cross section ( ) a measure of reaction probability Thermal neutron cross sections ( c) Thermal neutron cross section for fission ( f) 1 H 2 H 12 C 14 N 16 O 113 Cd c /b 0. 33 0. 00052 0. 0034 19, 820 Moderators: H 2 O vs. D 2 O vs. C 1. 82 0. 0002

Thermal Neutrons Cross Sections The extremely large thermal neutron cross section of 113 Cd makes cadmium a good neutron absorber or eliminator. Neutrons Capture Cross Sections of Cadmium Isotopes 106 Cd 108 Cd 110 Cd 111 Cd 112 Cd 113 Cd 114 Cd c / b 1 1 0. 1 24 2. 2 19, 820 0. 3 113 Cd (n, ) 114 Cd leads to the neutron-capture reaction Abundance/% 1. 25 0. 89 12. 45 12. 80 24. 13 12. 22 a stable 28. 37 isotope. These properties made cadmium a very desirable material for the nuclear technology industry.

Conclusion: Slow neutrons (0. 03 to 0. 001 e. V) are more effective for inducing fission of 235 U Fast neutrons (10 Me. V to 10 Ke. V) favours neutron capture reaction of 238 U Light atoms are effective moderators

2. 2 Radiation interaction with Matter 1) 2) 3) 4) overview Photon Interactions Neutron Interactions Interaction of Heavy Charged Particles with Matter 5) Scattering of Electrons in a Medium

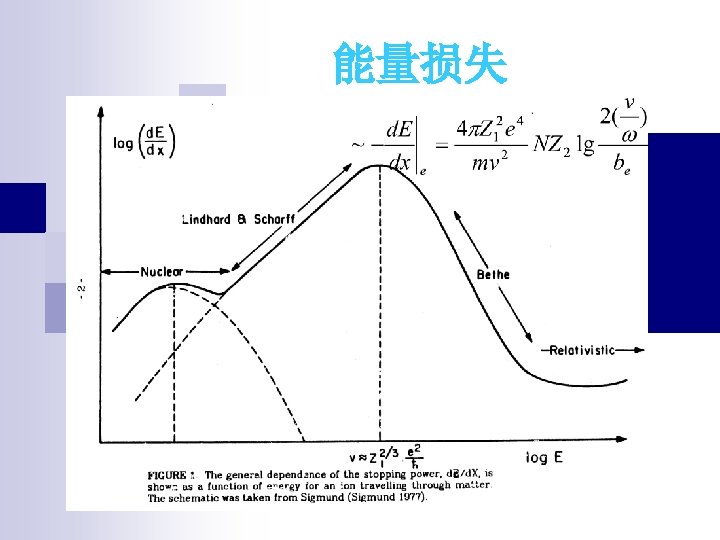
4) Interaction of Heavy Charged Particles with Matter Fast moving protons, 4 He, and other nuclei are heavy charged particles. Coulomb force dominates charge interaction. They ionize and excite (give energy to) molecules on their path. The Born-Bethe Formula for Energy Loss of Charged Particles.

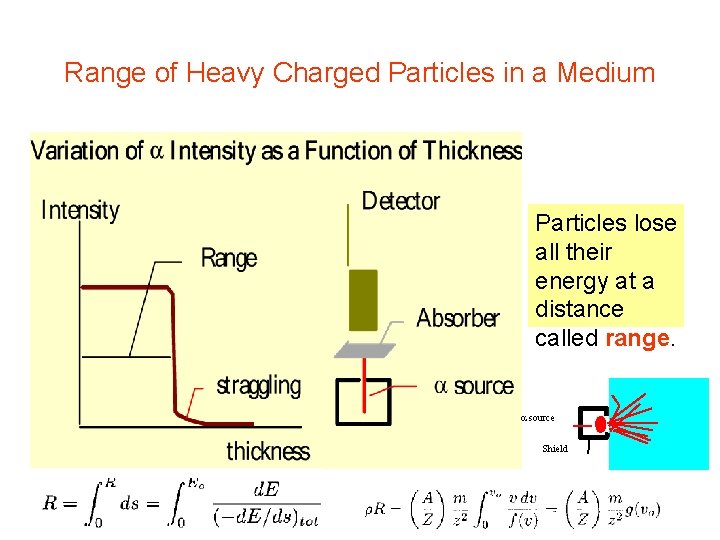
Range of Heavy Charged Particles in a Medium Particles lose all their energy at a distance called range. source Shield

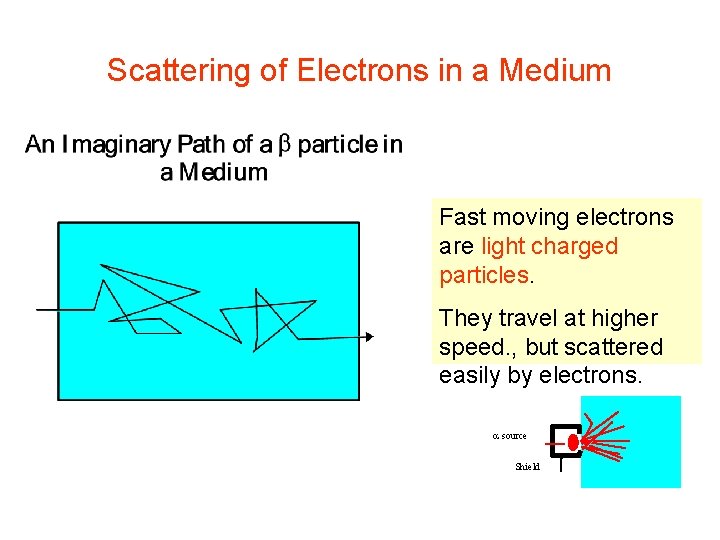
Scattering of Electrons in a Medium Fast moving electrons are light charged particles. They travel at higher speed. , but scattered easily by electrons. source Shield

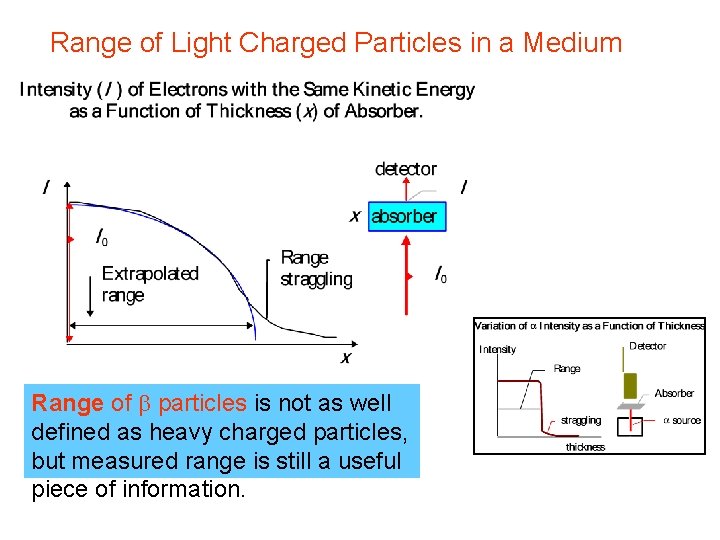
Range of Light Charged Particles in a Medium Range of b particles is not as well defined as heavy charged particles, but measured range is still a useful piece of information.

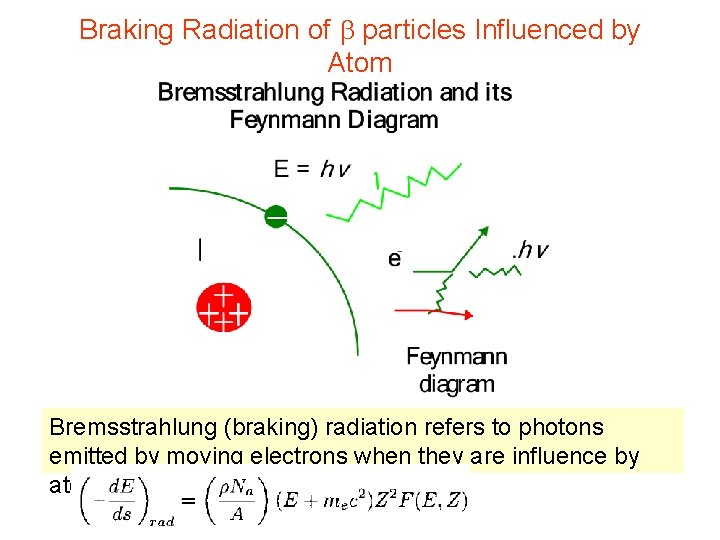
Braking Radiation of b particles Influenced by Atom Bremsstrahlung (braking) radiation refers to photons emitted by moving electrons when they are influence by atoms.

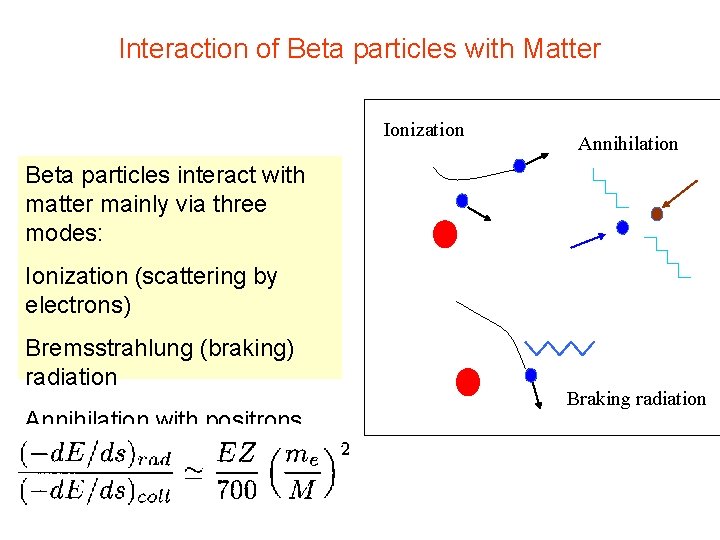
Interaction of Beta particles with Matter Ionization Annihilation Beta particles interact with matter mainly via three modes: Ionization (scattering by electrons) Bremsstrahlung (braking) radiation Annihilation with positrons Braking radiation

Example : At what energy does an electron moving through gold lose as much energy by bremsstrahlung as it does by ionizing and exciting gold atoms? For gold Z = 79 and for equal energy loss by both mechanisms, we have find for electrons M = me that E = 700/79 = 8. 9 Me. V.

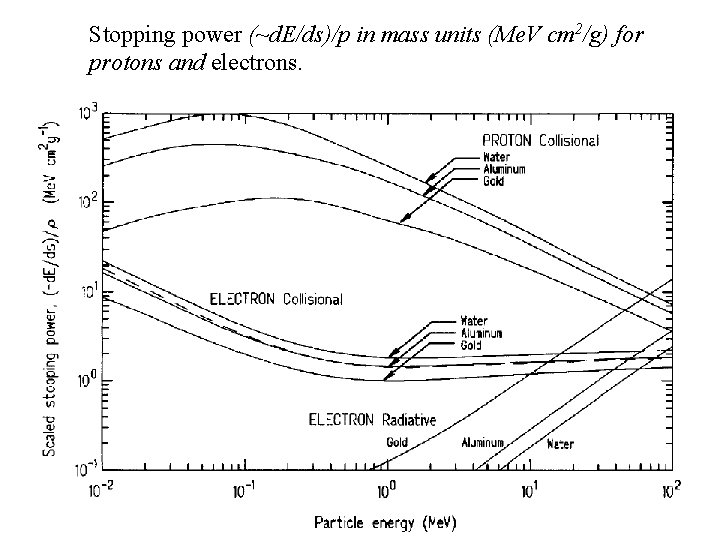
Stopping power (~d. E/ds)/p in mass units (Me. V cm 2/g) for protons and electrons.

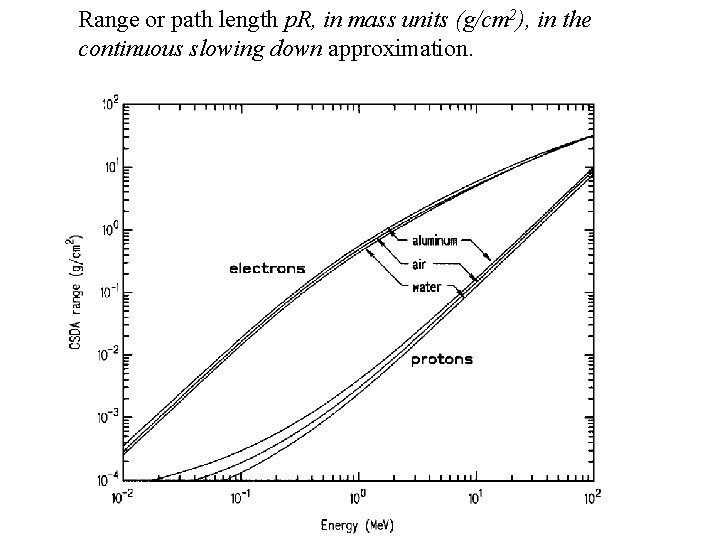
Range or path length p. R, in mass units (g/cm 2), in the continuous slowing down approximation.

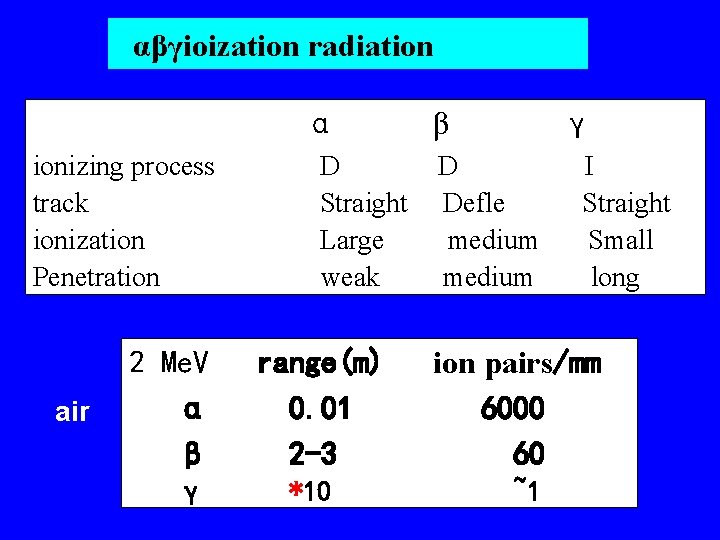
αβγioization radiation α ionizing process track ionization Penetration air 2 Me. V α β γ D Straight Large weak range(m) 0. 01 2 -3 *10 β γ D Defle medium I Straight Small long ion pairs/mm 6000 60 ~1

2. 2 Radiation interaction with Matter 1) 2) 3) 4) overview Photon Interactions Neutron Interactions Interaction of Heavy Charged Particles with Matter 5) Scattering of Electrons in a Medium


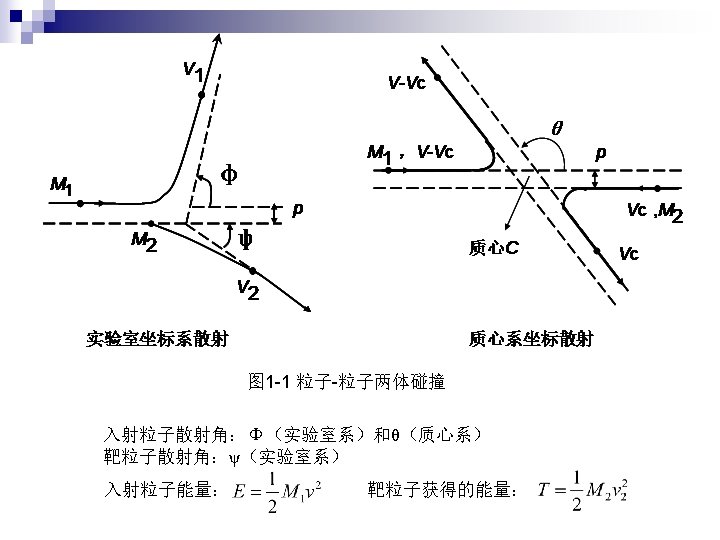
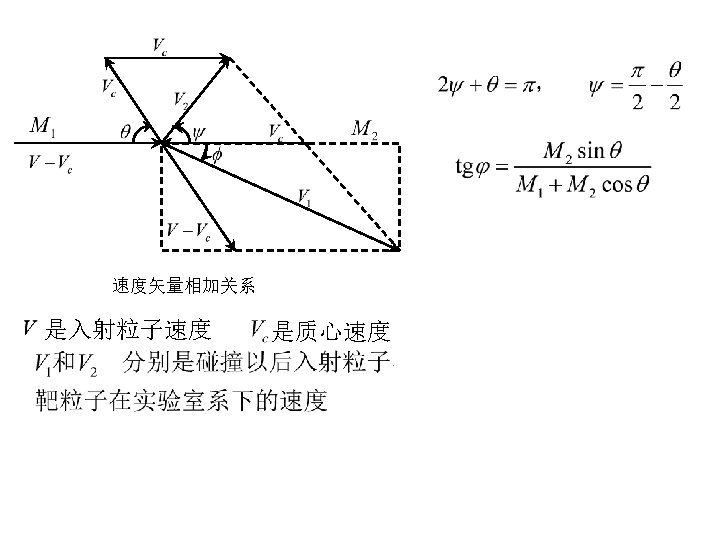
n 2. 1 Two-body collisions Formula Tacit assumptions: Well defined Z 1 Independent two body collisions Stochastic process, average E. L. n 2. 2 Collisions with atoms Elastic and inelastic energy loss n 2. 3 Adiabatic cutoff Momentum approximation free Harmonic model free bounded n 2. 4 Under which circumstances is classical mechanics applicable

两体碰撞 INCIDENT ION BEAM



靶粒子得到的能量 b: collision diameter Closest distance in repulsive potential


2. 2 Collisions with atoms Elastic and inelastic energy loss n Elastic moving the center of the mass of the atom-- nuclei n Inelastic leading to excitation of internal degrees of freedom--electrons


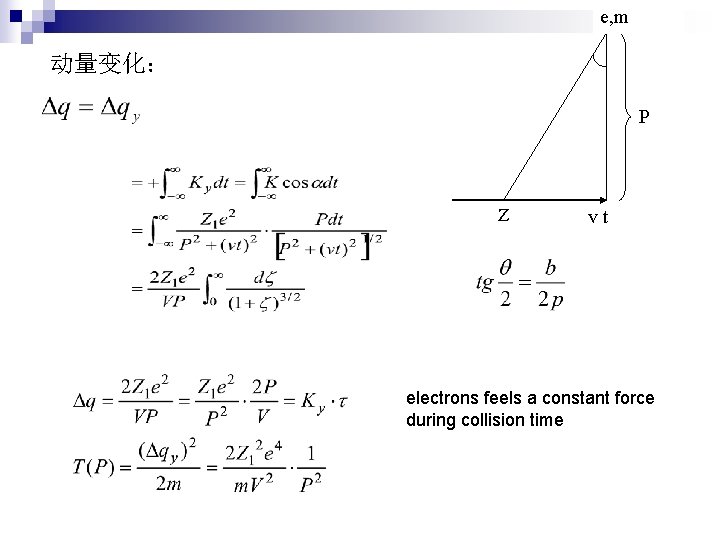
e, m 动量变化: P Z vt electrons feels a constant force during collision time

谐振子模型: 运动方程: 令: y the distance of the electron away from the equilibrium position mÿ=-mω2 y+K 0≤t ≤τ 初条件: mÿ 1= - mω2 y 1 y=0



2. 4 Under which circumstances is classical mechanics applicable
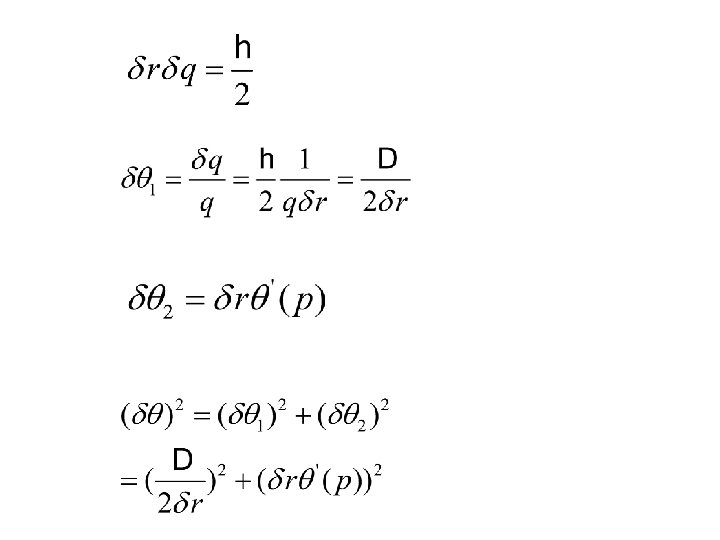
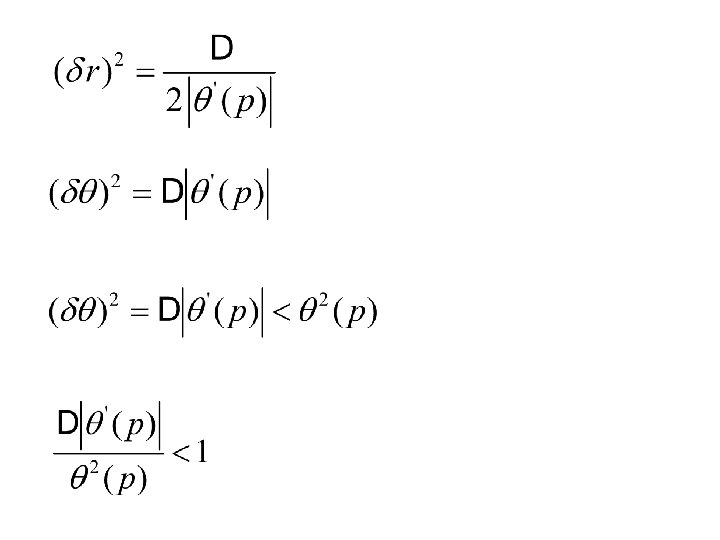
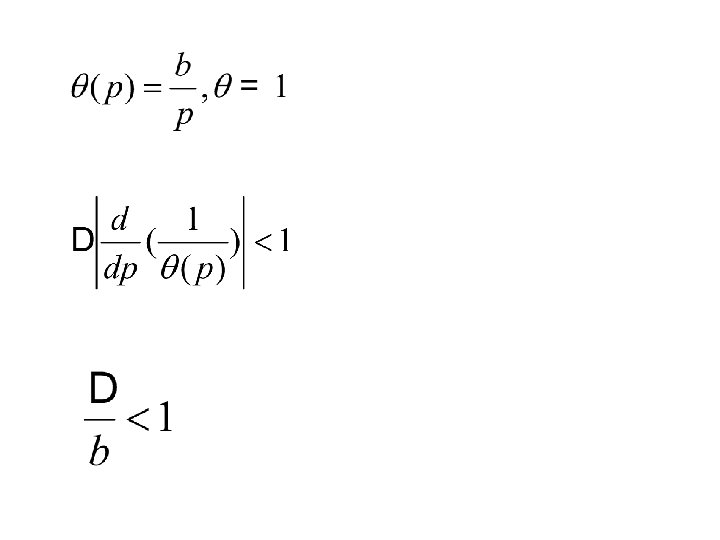


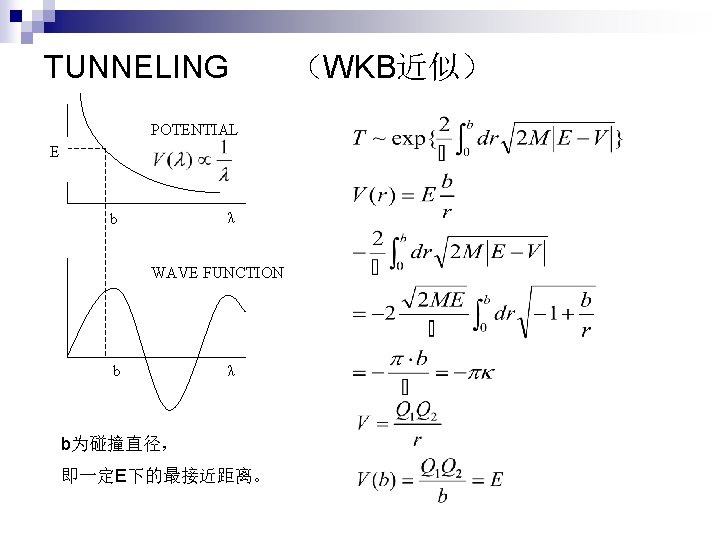
TUNNELING POTENTIAL E λ b WAVE FUNCTION b λ b为碰撞直径, 即一定E下的最接近距离。 (WKB近似)

2. 2 Radiation interaction with Matter 1) 2) 3) 4) overview Photon Interactions Neutron Interactions Attenuation of Charged Particles