Chapter 2 Prospect Theory and Expected Utility Theory

Chapter 2 Prospect Theory and Expected Utility Theory 1

A. Von-Neumann-Morgenstern Expected Utility Theory 1. Von-Neumann-Morgenstern Axioms : Certain, identifiable Outcomes C: Choice facing the individual 2

A. Von-Neumann-Morgenstern Expected Utility Theory 2. Utility Function Let be the number described in A(σ) Define u over all possible choices by Where 3

A. Von-Neumann-Morgenstern Expected Utility Theory 3. Expected Utility Theory ~ 4

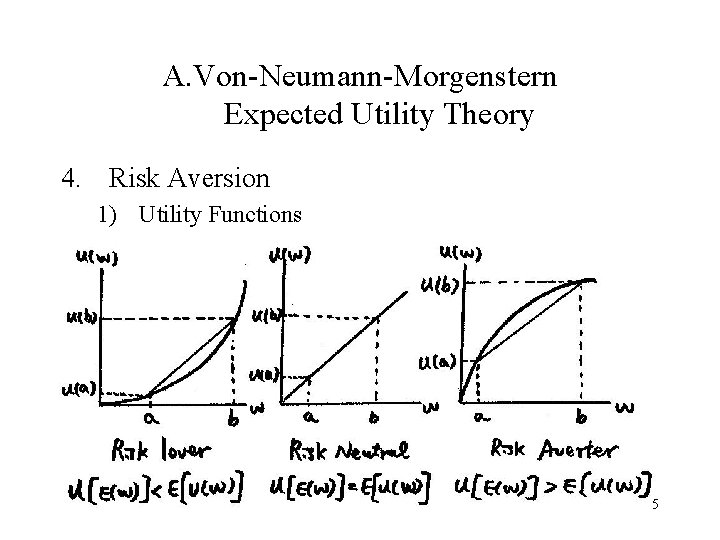
A. Von-Neumann-Morgenstern Expected Utility Theory 4. Risk Aversion 1) Utility Functions 5

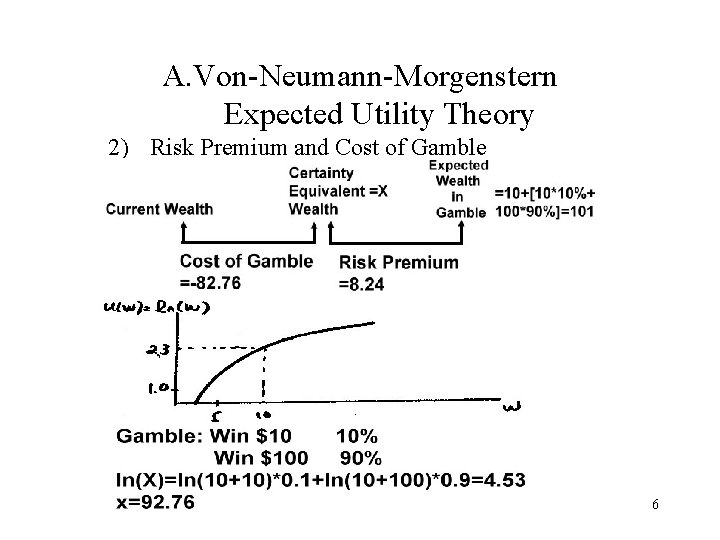
A. Von-Neumann-Morgenstern Expected Utility Theory 2) Risk Premium and Cost of Gamble 6

A. Von-Neumann-Morgenstern Expected Utility Theory 3) Pratt-Arrow Risk Aversion Def. Assume that an individual faces an “actuarially fair” bet (i. e. ). Let w be the individual’s initial wealth. The risk premium is that amount such that the individual is indifferent between receiving the risk and receiving the nonrandom amount. 7

A. Von-Neumann-Morgenstern Expected Utility Theory • RHS • LHS 8

A. Von-Neumann-Morgenstern Expected Utility Theory • ARA= Absolute Risk Aversion • RRA= Relative Risk Aversion 9

A. Von-Neumann-Morgenstern Expected Utility Theory • E. g. 1. Quadratic Utility function • E. g. 2. Power Utility function 10

A. Von-Neumann-Morgenstern Expected Utility Theory 5. Mean-Variance(M-V) Utility function – Assume – Indifference curves of risk averters: 11

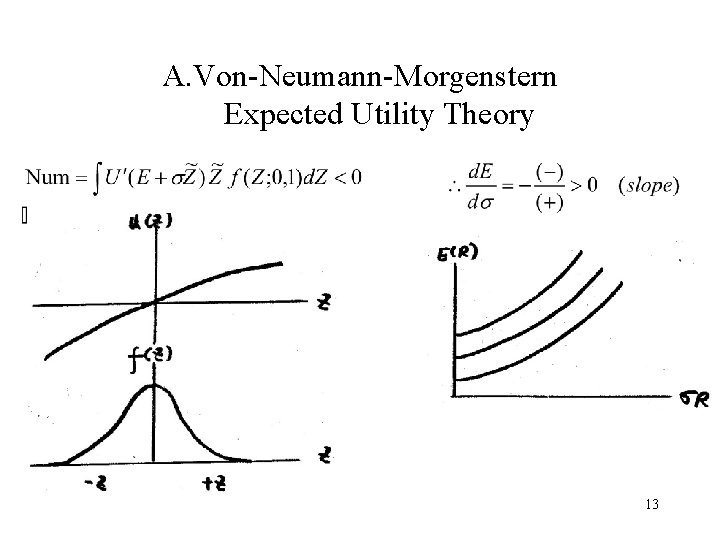
A. Von-Neumann-Morgenstern Expected Utility Theory (+) ? (+) 12

A. Von-Neumann-Morgenstern Expected Utility Theory 13

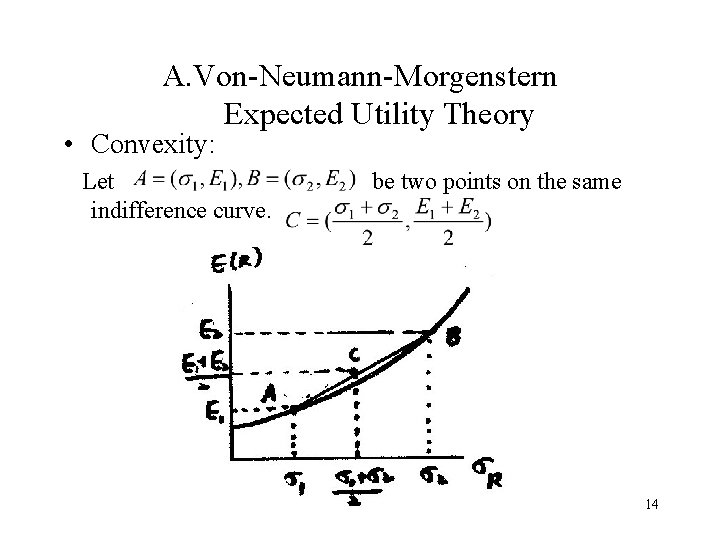
A. Von-Neumann-Morgenstern Expected Utility Theory • Convexity: Let indifference curve. be two points on the same 14

A. Von-Neumann-Morgenstern Expected Utility Theory 15

A. Von-Neumann-Morgenstern Expected Utility Theory 6. Stochastic Dominance 1) First Order Stochastic Dominance: An asset is said to be stochastically dominant over another if an individual receive greater wealth from it in every state of nature. Asset x, will be stochastically dominant over asset y, if 16

A. Von-Neumann-Morgenstern Expected Utility Theory 2) Second Order Stochastic Dominance An asset is said to be second order stochastically dominant over another if an individual (Risk averter) receives greater accumulated wealth in any given level of wealth. Asset x, is second order stochastically dominant over asset y, if 17

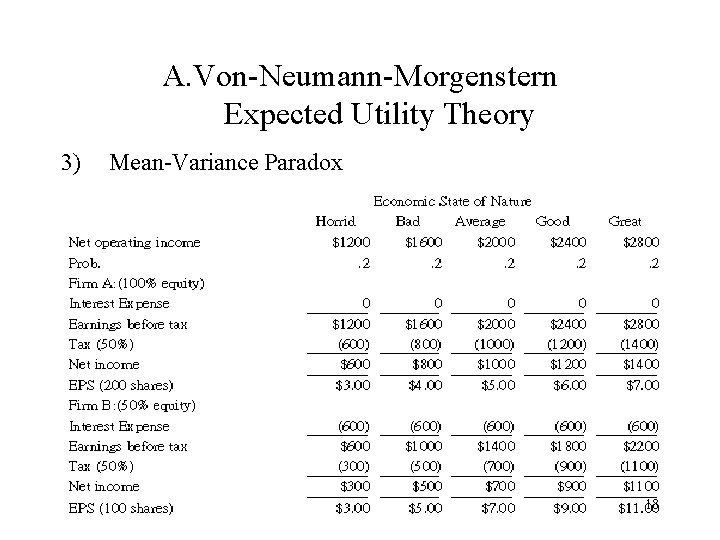
A. Von-Neumann-Morgenstern Expected Utility Theory 3) Mean-Variance Paradox 18

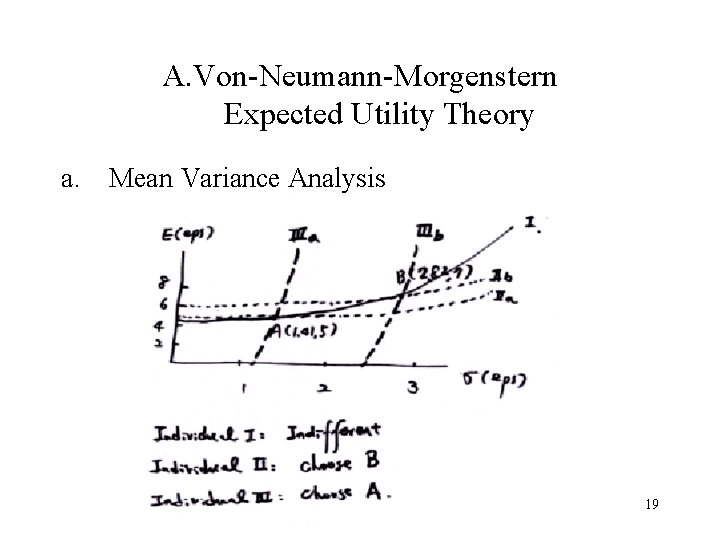
A. Von-Neumann-Morgenstern Expected Utility Theory a. Mean Variance Analysis 19

A. Von-Neumann-Morgenstern Expected Utility Theory a. Stochastic Dominance Analysis EPS Prob(B) Prob(A) F(B) G(A) F-G ∑(F-G) 3. 00 0. 2 0. 0 4. 00 0. 2 0. 4 -0. 2 5. 00 0. 2 0. 4 0. 6 -0. 2 -0. 4 6. 00 0. 2 0. 4 0. 8 -0. 4 -0. 8 7. 00 0. 2 0. 6 1. 0 -0. 4 -1. 2 8. 00 0. 6 1. 0 -0. 4 -1. 6 9. 00 0. 2 0. 0 0. 8 1. 0 -0. 2 -1. 8 10. 00 0. 8 1. 0 -0. 2 -2. 0 11. 00 2. 0 0. 0 1. 0 0. 0 -2. 0 20

B. Kahneman and Tversky Prospect Theory ---Non-expected Utility Theory 1. Three effects 1) Certainty effect 21

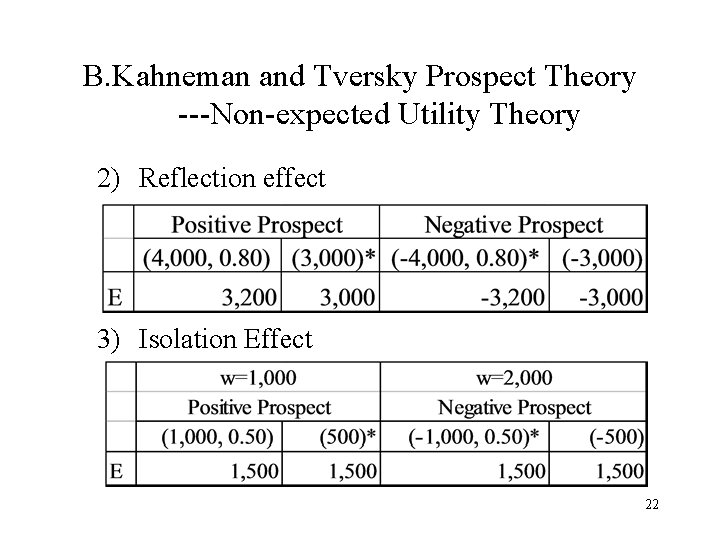
B. Kahneman and Tversky Prospect Theory ---Non-expected Utility Theory 2) Reflection effect 3) Isolation Effect 22

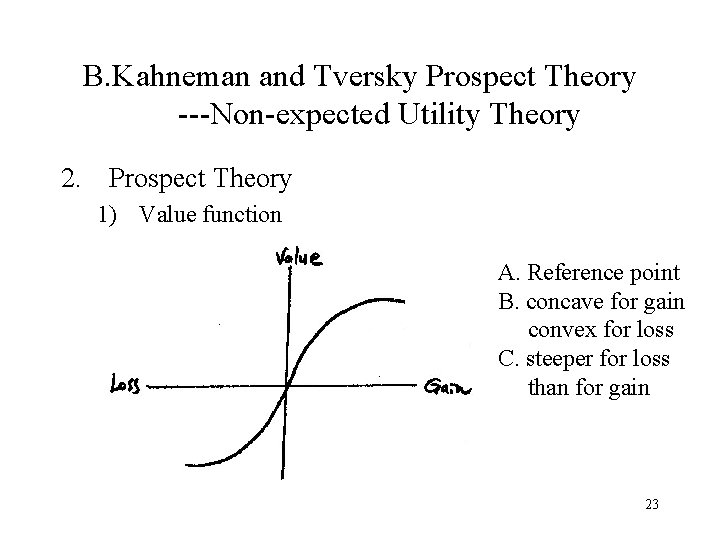
B. Kahneman and Tversky Prospect Theory ---Non-expected Utility Theory 2. Prospect Theory 1) Value function A. Reference point B. concave for gain convex for loss C. steeper for loss than for gain 23

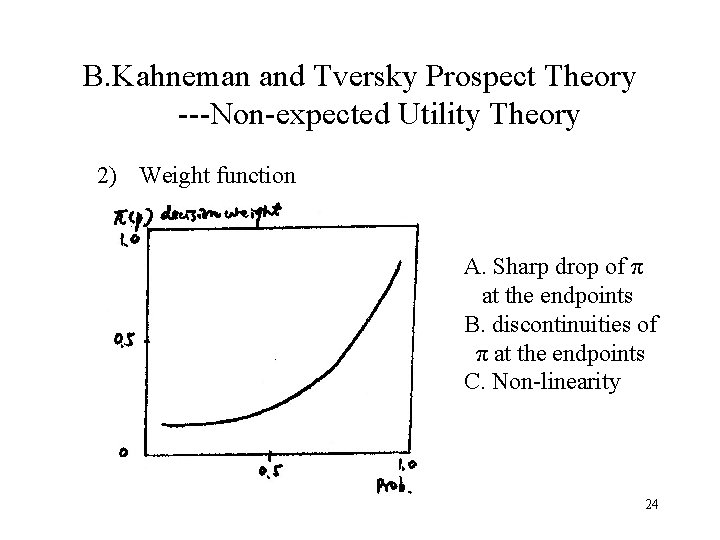
B. Kahneman and Tversky Prospect Theory ---Non-expected Utility Theory 2) Weight function A. Sharp drop of π at the endpoints B. discontinuities of π at the endpoints C. Non-linearity 24