Chapter 2 Particle Properties of Waves Electromagnetic Waves

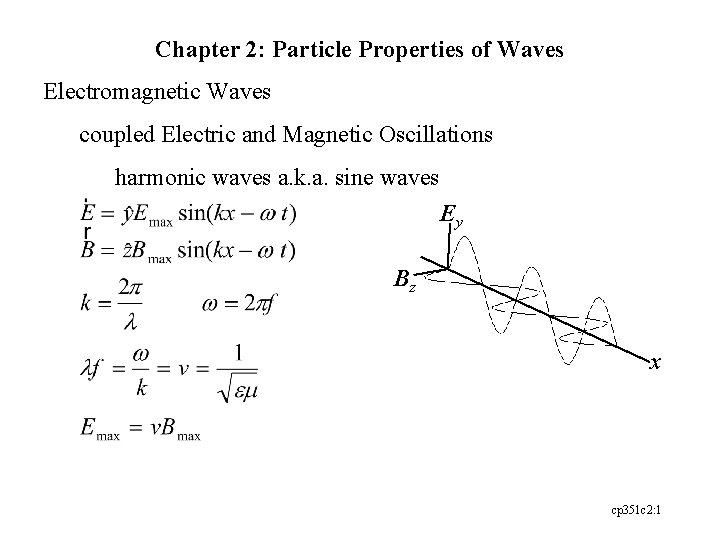
Chapter 2: Particle Properties of Waves Electromagnetic Waves coupled Electric and Magnetic Oscillations harmonic waves a. k. a. sine waves Ey Bz x cp 351 c 2: 1

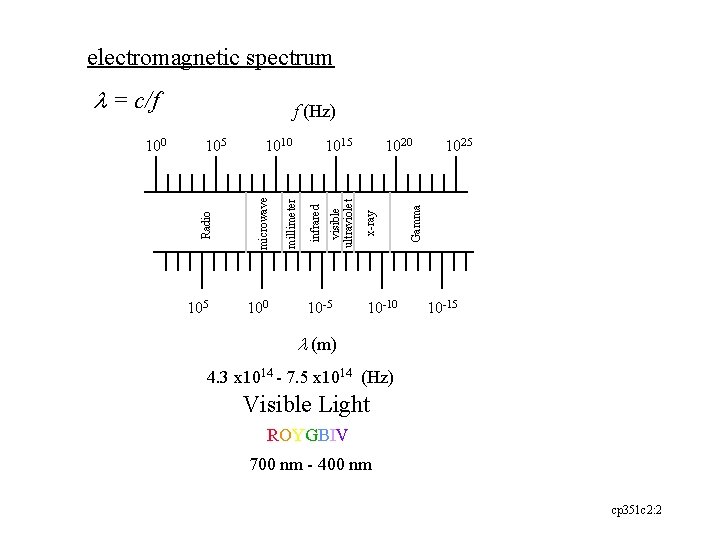
electromagnetic spectrum l = c/f 105 100 10 -5 10 -10 1025 Gamma 1020 x-ray visible ultraviolet infrared 1015 millimeter 1010 microwave 105 Radio 100 f (Hz) 10 -15 l (m) 4. 3 x 1014 - 7. 5 x 1014 (Hz) Visible Light ROYGBIV 700 nm - 400 nm cp 351 c 2: 2

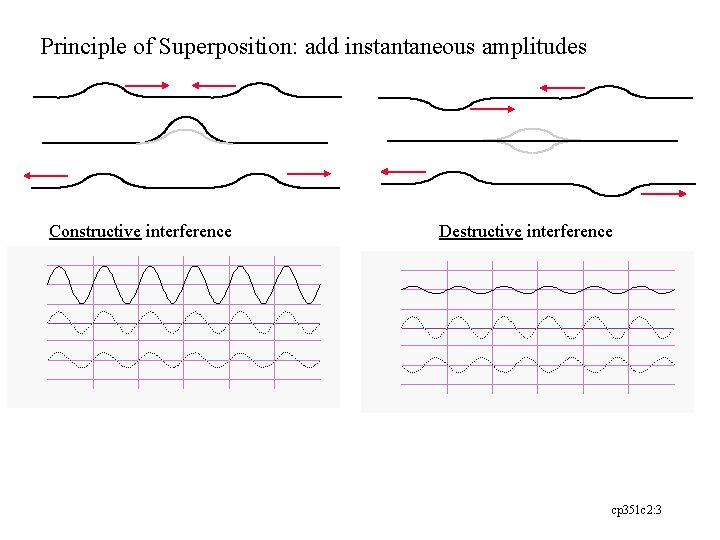
Principle of Superposition: add instantaneous amplitudes Constructive interference Destructive interference cp 351 c 2: 3

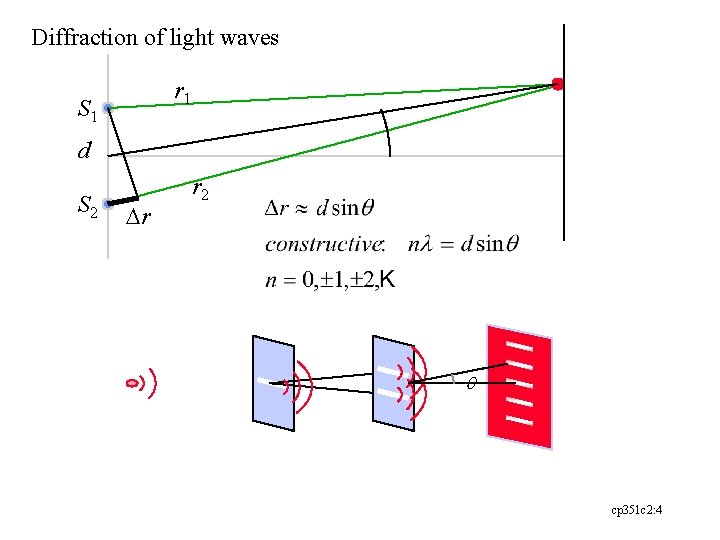
Diffraction of light waves r 1 S 1 d S 2 Dr r 2 q cp 351 c 2: 4

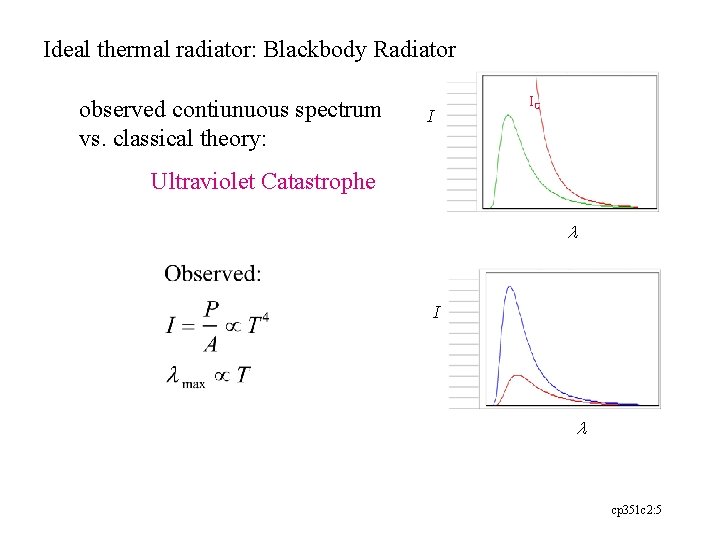
Ideal thermal radiator: Blackbody Radiator observed contiunuous spectrum vs. classical theory: IC I Ultraviolet Catastrophe l I l cp 351 c 2: 5

Theoretical black body: standing wave modes in a (3 -d) cavity cp 351 c 2: 6

Example 2. 1 A certain 660 Hz tuning fork can be considered as a harmonic oscillator with a vibrational energy of 0. 04 J. Compare its energy quantum of energy for the tuning fork with its vibrational energy. Compare the fork’s quantum of energy with those of an atomic oscillator which emits a frequency of 5. 00 x 14 Hz. cp 351 c 2: 7

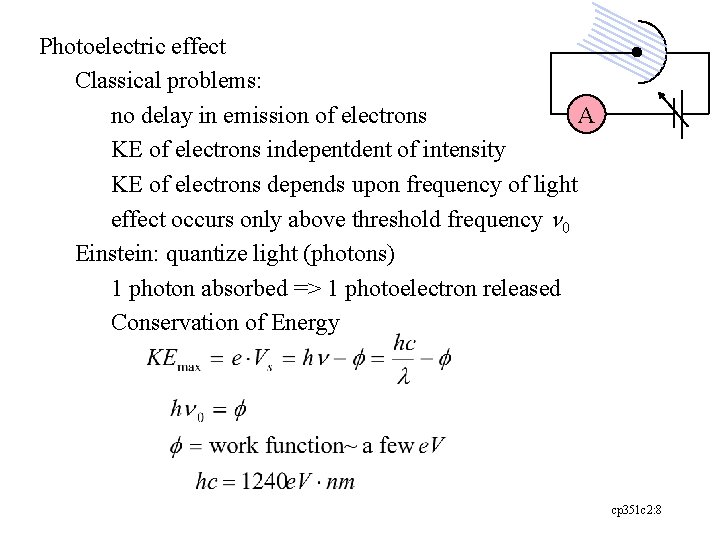
Photoelectric effect Classical problems: A no delay in emission of electrons KE of electrons indepentdent of intensity KE of electrons depends upon frequency of light effect occurs only above threshold frequency n 0 Einstein: quantize light (photons) 1 photon absorbed => 1 photoelectron released Conservation of Energy cp 351 c 2: 8

Example 2. 2 Ultraviolet light of wavelength 350 nm and an intensity of 1. 00 W/m 2 is directed at a potassium surface (f = 2. 2 e. V). (a) Find the maximum KE of the photoelectrons. (b) If 0. 50 percent of the incident photons produce photoelectrons, how many are emitted per second if the potassium surface area is 1. 0 cm 2? Thermionic Emission: k. T ~ f => random motion kicks electrons loose Wave-particle “duality” interference and diffraction: wave phenomena photoelectric effect, etc. : particle phenomena => intensity ~ probability for individual photons cp 351 c 2: 9

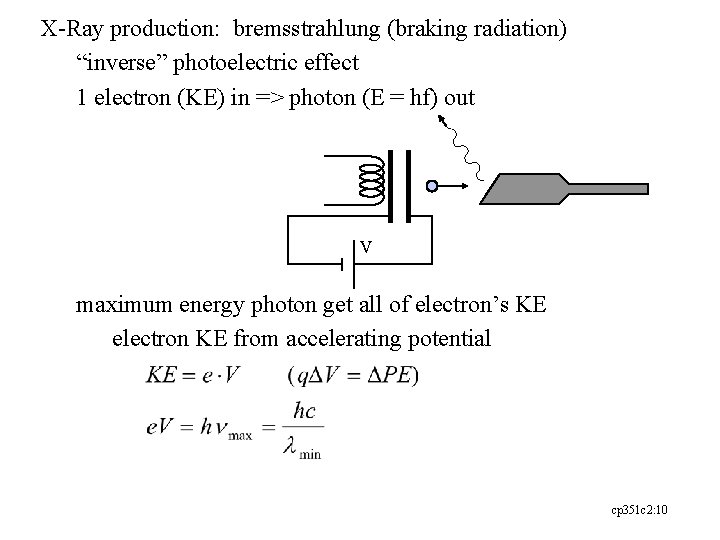
X-Ray production: bremsstrahlung (braking radiation) “inverse” photoelectric effect 1 electron (KE) in => photon (E = hf) out V maximum energy photon get all of electron’s KE electron KE from accelerating potential cp 351 c 2: 10

Example 2. 3 Find the shortest wavelength present in the radiation from an X-ray machine whose accelerating potential is 50 k. V. cp 351 c 2: 11

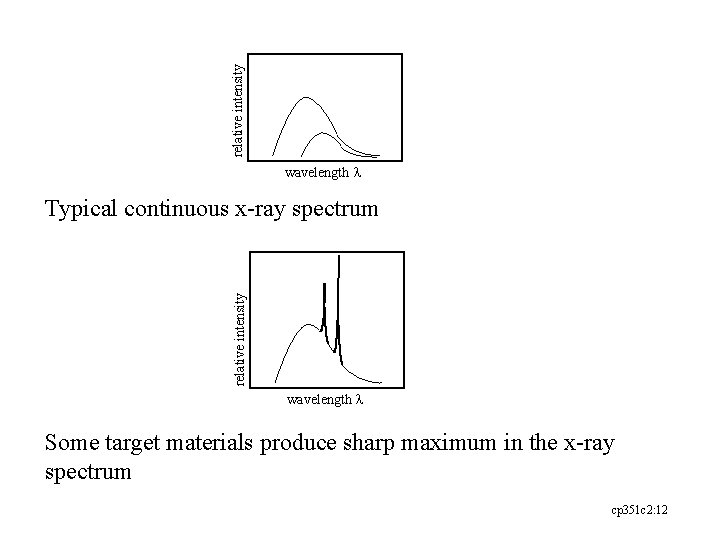
relative intensity wavelength l relative intensity Typical continuous x-ray spectrum wavelength l Some target materials produce sharp maximum in the x-ray spectrum cp 351 c 2: 12

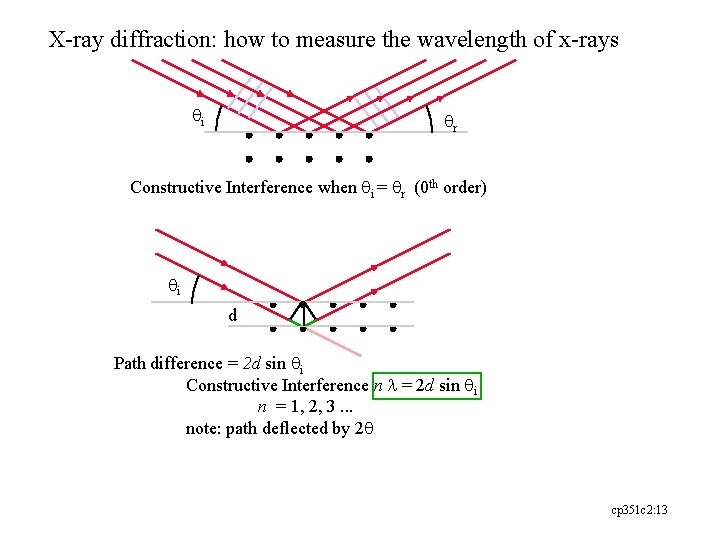
X-ray diffraction: how to measure the wavelength of x-rays qi qr Constructive Interference when qi = qr (0 th order) qi d Path difference = 2 d sin qi Constructive Interference n l = 2 d sin qi n = 1, 2, 3. . . note: path deflected by 2 q cp 351 c 2: 13

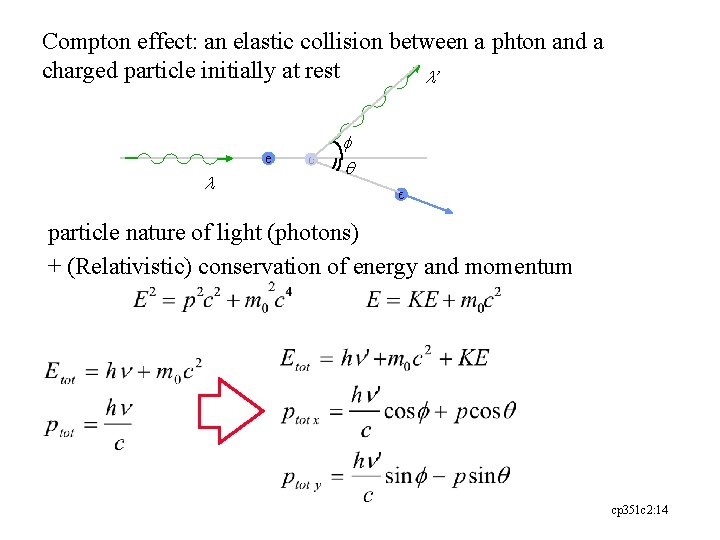
Compton effect: an elastic collision between a phton and a charged particle initially at rest l’ e l e f q e particle nature of light (photons) + (Relativistic) conservation of energy and momentum cp 351 c 2: 14

l. C = 2. 426 pm for electrons cp 351 c 2: 15

Example 2. 4 X-rays of wavelength 10. 0 pm are scattered from a target. (a) Find the wavelength of the x-rays scattered through an angle of 45 degrees. (b) Find the maximum wavelength of the scattered x-rays. (c) Find the maximum KE of the recoil electrons. cp 351 c 2: 16

pair production: conservation of energy, momentum + other conservation laws E = mc 2 l N p e+ e e- creation of particle and antiparticle (antimatter) antiparticle has same mass, opposite charge etc. particle/antiparticle pair can anihilate to create a pair of photons: e + + e - -> g + g cp 351 c 2: 17

Example 2. 5: Show that pair production cannot occur in empty space. (Hint: look at relativistic conservation of energy and momentum) Example 2. 6: An electron and a positron are moving side by side in the +x direction at 0. 500 c when they annihilate each other. Two photons are produced that move along the x -axis. (a) Do both photons move in the +x direction? (b) What is the energy of each photon? cp 351 c 2: 18

Photon Absorption Three chief mechanisms for x-ray and gamma ray photons to interact with matter photoelectric effect (photon absorbed) Compton scattering (photon energy decreased) pair production (photon converted to pair) The dominant mechanism depends upon material and photon energy A slab of material will reduce intensity: cp 351 c 2: 19

Example 2. 7: The linear attenuation coefficient for 2. 0 Me. V gamma rays in water is 4. 9 m-1. (a) Find the relative intensity of the gamma rays after it has passed through 10 cm of water. (b) How far must the beam travel in water before being reduced to 1 percent of its original value? Problems: 2, 5, 6, 8, 11, 12, 15, 17, 19, 20, 21, 22, 23, 26, 27, 29, 32, 39, 43, 45, 46, 47 skip 2. 9 or read at your liesure cp 351 c 2: 20