Chapter 2 Part 3 Antenna Chapter Outlines Chapter

Chapter 2 (Part 3) Antenna

Chapter Outlines Chapter 2 PART 3 Antennas Ø Ø Dipole & Monopole Fundamental Parameters of Antennas Electrically Short Antennas Dipole Antennas Monopole Antennas 2

Introduction Wires passing an alternating current emit or radiate EM energy. The shape and size of the current carrying structure determine how much energy is radiated, direction of propagation and how well the radiation is captured. Henceforth, the structure to efficiently radiate in a preferred direction is called transmitting antenna, while the other side which is to capture radiation from preferable direction is called receiving antenna. In most cases, the efficiency and directional nature for an antenna is the same whether its receiving or transmitting. 3

Introduction (Cont’d. . ) Common types of antennas: 4

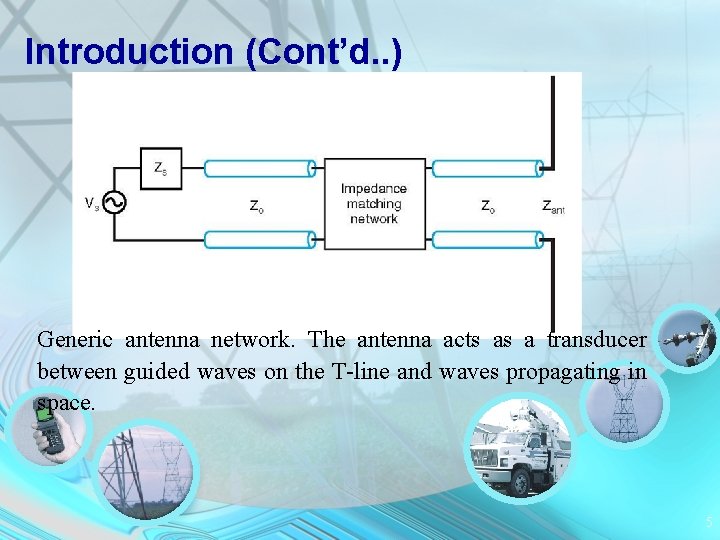
Introduction (Cont’d. . ) Generic antenna network. The antenna acts as a transducer between guided waves on the T-line and waves propagating in space. 5

4. 1 Fundamental Parameters of Antennas To describe the performance of an antenna, definitions of various parameters are discussed. The radiated power, beam pattern, directivity, and efficiency are all important parameters in characterizing antenna. RADIATED POWER Suppose transmitting antenna located at the origin of spherical coordinate. From this coordinate system, there are three components of radiated field, in r, θ and φ. But, the intensities of these components vary with radial distance as 1/r, 1/r 2 and 1/r 3.

Fundamental Parameters of Antennas (Cont’d. . ) For almost all practical applications, a receiving antenna located far enough away from the transmitter (as a point source of radiation) far field region. A distance r from the origin is generally accepted as being in the far field region if : L is the length of the largest dimension on the antenna element, and assumed L>λ. For smaller L, r should at least as large as λ

Fundamental Parameters of Antennas (Cont’d. . ) In the far field, the radiated waves resemble plane waves propagating in ar direction where time harmonic fields related by : The time averaged power density vector of the wave is by Poynting Theorem, Where in the far field,

Fundamental Parameters of Antennas (Cont’d. . ) So, the total power radiated by the antenna, Prad is found by integrating it over a close spherical surface :

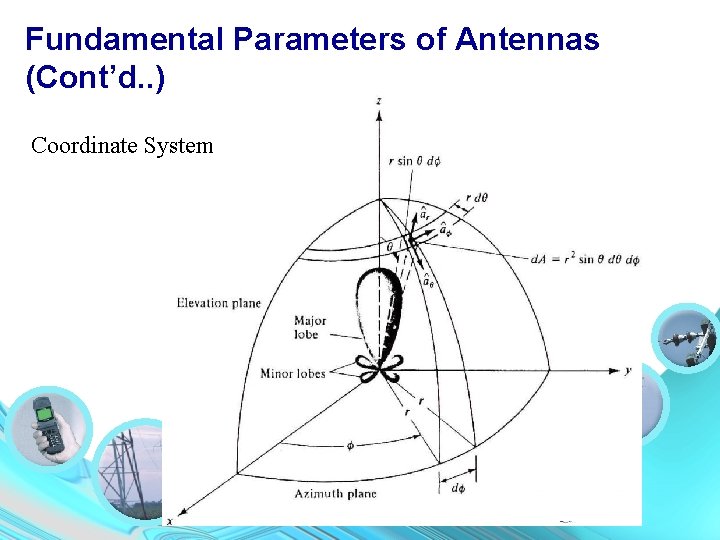
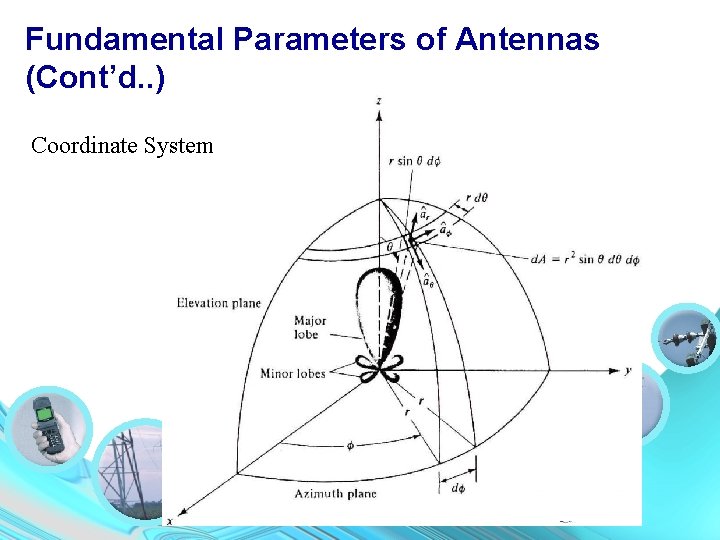
Fundamental Parameters of Antennas (Cont’d. . ) Coordinate System

Example 1 In free space, suppose a wave propagating radially away from an antenna at the origin has: Where the driving current phasor Find: a) ES b) P(r, φ, θ) c) Prad and Rrad 11

Solution to Example 1 To find ES, from time harmonic fields relation: So, Then, to find P(r, φ, θ)

Solution to Example 1 (Cont’d. . ) Then, Solving:

Fundamental Parameters of Antennas (Cont’d. . ) RADIATION PATTERNS A mathematical and/or graphical representation of the radiation properties of an antenna, such as the: • Amplitude • Phase • Polarization, etc. as a function of angular space coordinates θ, φ

Fundamental Parameters of Antennas (Cont’d. . ) Radiation patterns usually indicate either electric field, E intensity or power intensity. Magnetic field intensity, H has the same radiation pattern as E related by η 0. The polarization or orientation of the E field vector is an important consideration in an E field plot. A transmit receive antenna pair must share same polarization for the most efficient communication. Field Pattern Power Pattern A plot of the field (either electric |E| or magnetic |H|) on a linear scale A plot of the power (proportional to either the electric |E|2 or magnetic |H|2) on a linear scale or decibel (d. B) scale

Fundamental Parameters of Antennas (Cont’d. . ) Coordinate System

Fundamental Parameters of Antennas (Cont’d. . ) Since the actual field intensity is not only depends on radial distance, but also on how much power delivered to antenna, we use and plot normalized function divide the field or power component with its maximum value. E. g. the normalized power function or normalized radiation intensity :

Fundamental Parameters of Antennas (Cont’d. . ) If the antenna radiates EM waves equally in all directions, it is termed as isotropic antenna, where the normalized power function is equal to 1. So, In contrast with isotropic antenna, a directional antenna radiates and receives preferentially in some direction.

Fundamental Parameters of Antennas (Cont’d. . ) The normalized radiation patterns for a generic antenna, called polar plot. A 3 D plot of radiation pattern can be difficult to generate and work with, so take slices of the pattern and generate 2 D plots (rectangular plots) for all θ at φ=π/2 and φ=3π/2 Polar plot Rectangular plot (in d. B)

Fundamental Parameters of Antennas (Cont’d. . )

Fundamental Parameters of Antennas (Cont’d. . ) The polar plot also can be in terms of d. B. Where normalized E field pattern, This will be identical to the power pattern in decibels if: whereas

Fundamental Parameters of Antennas (Cont’d. . ) The are some zeros and nulls in radiation pattern, indicating no radiations. These lobes shows the direction of radiation, where main or major lobe lies in the direction of maximum radiation. The other lobes divert power away from the main beam, so that good antenna design will seek to minimize the side and back lobes. Beam’s directional nature is beamwidth, or half power beamwidth or 3 d. B beamwidth. It will shows the angular width of the beam measured at the half power or -3 d. B points.

Fundamental Parameters of Antennas (Cont’d. . ) For linearly polarized antenna, performance is often described in terms of its principal E and H plane patterns. E plane : the plane containing the E field vector & the direction of max radiation H plane : the plane containing the H field vector & the direction of max radiation For next figure, • the x-z plane (elevation plane, φ=0) is the principal E-plane • the x-y plane (azimuthal plane; θ=π/2) is the principal H-plane.

Fundamental Parameters of Antennas (Cont’d. . )

Fundamental Parameters of Antennas (Cont’d. . ) For this figure, • Infinite number of principal Eplanes (elevation plane, φ=φc). • One principal H-plane (azimuthal plane; θ=π/2).

Fundamental Parameters of Antennas (Cont’d. . ) DIRECTIVITY A measure of how well an antenna radiate most of the power fed into the main lobe. Before defining directivity, describe first the antenna’s pattern solid angle or beam solid angle. An arc with length equal to a circle’s radius defines a radian.

Fundamental Parameters of Antennas (Cont’d. . ) An area equal to the square of a sphere’s radius defines a steradian (sr). A differential solid angle dΩ in sr is: For sphere, the solid angle is found by integrating dΩ :

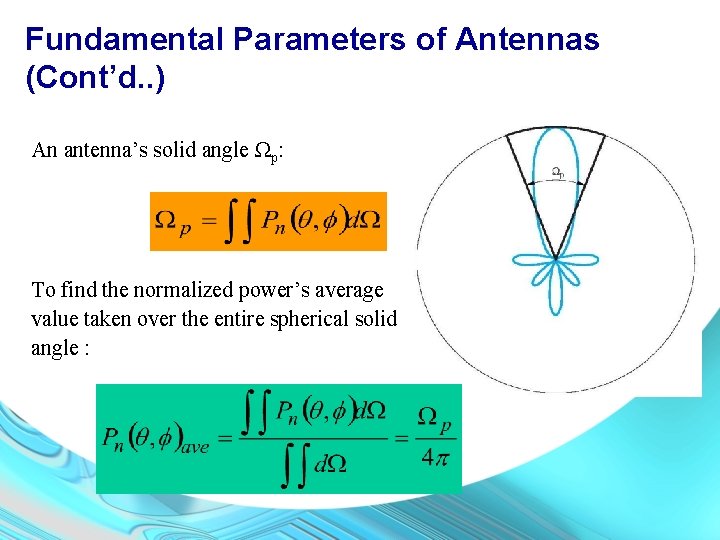
Fundamental Parameters of Antennas (Cont’d. . ) An antenna’s solid angle Ωp: To find the normalized power’s average value taken over the entire spherical solid angle :

Fundamental Parameters of Antennas (Cont’d. . ) The directive gain D(θ, φ) of an antenna is the ratio of the normalized power in particular direction to the average normalized power : The directivity Dmax is the maximum directive gain, So,

Fundamental Parameters of Antennas (Cont’d. . ) Directivity in decibels as: Useful relation: Total radiated power as: Or :

Fundamental Parameters of Antennas (Cont’d. . ) For (a), power gets radiated to the side and back lobes, so the pattern solid angle is large and the directivity is small. For (b), almost all the power gets radiated to the main beam, so pattern solid angle is small and directivity is high.

Example 2 For this normalized radiation intensity, Find the beamwidth, pattern solid angle and the directivity. 32

Solution to Example 2 The beam is pointing in the +y direction. Due to the beam having function in θ and φ, so that: From previous equation, so that a 3 d. B beamwidth is at half of total power = 0. 5. 33

Solution to Example 2 (Cont’d. . ) To find BWθ, we fix φ = π/2 to get: and then set sin 2θ equal to ½. Then, To find BWφ, we fix θ = π/2 to get: 34

Solution to Example 2 (Cont’d. . ) and then set sin 3θ equal to ½. Then, So, The pattern solid angle is:

Solution to Example 2 (Cont’d. . ) Where each integral is solved as follows: Please continue on your own!! So, Finally, and the directivity, 36

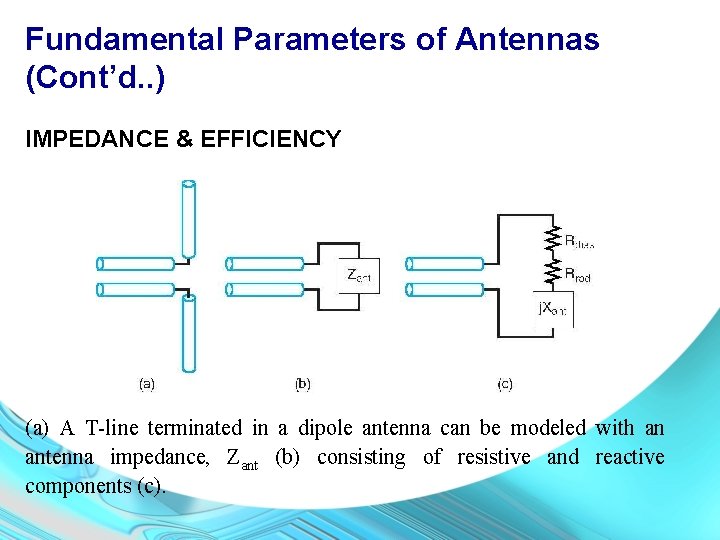
Fundamental Parameters of Antennas (Cont’d. . ) IMPEDANCE & EFFICIENCY (a) A T-line terminated in a dipole antenna can be modeled with an antenna impedance, Zant (b) consisting of resistive and reactive components (c).

Fundamental Parameters of Antennas (Cont’d. . ) The antenna resistance consists of radiation resistance Rrad and a dissipative resistance Rdiss that arises from ohmic losses in the metal conductor. For antenna driven by phasor current, and also For maximum radiated power, Rrad need to be as large as possible but without being too large, for ease of matching with the feedline.

Fundamental Parameters of Antennas (Cont’d. . ) So then the antenna efficiency, e The power gain G(θ, φ) is likely its directive gain plus efficiency, where: And the max power gain is when the directivity is max. It’s been always expressed in d. Bi, indicating d. B with respect to an isotropic antenna.

4. 2 Electrically Short Antennas If the current distribution of a radiating element is known, it’s possible to calculate the radiated fields by a direct integration but, the integrals can be very complex. For time harmonic fields, integration is performed to find a phasor called retarded vector magnetic potential, which then followed by simple differentiation to find the H field. We will begin with a derivation of the retarded vector magnetic potential, then find the radiated fields for Hertzian dipole (infinitesimally short element with uniform current along its length). From that, we can find the fields from longer structures via integration e. g. small loop antenna.

Electrically Short Antennas (Cont’d. . ) Vector Magnetic Potential In working with electric fields, and analogous term for H field is the vector magnetic potential A, often used for antenna calculations. Where in the point form of Gauss Law for magnetic fields, With vector identity that states the div of the curl of any vector A is zero. So, Then we now seek a relation between vector A and a current source.

Electrically Short Antennas (Cont’d. . ) From Biot Savart law, Remember? !? The vector magnetic potential at the observation point (o) results from a current density distributed about the volume vd.

Electrically Short Antennas (Cont’d. . ) Due to long derivation and by using vector identity, we could get: Refer to text book! Then, More properly, Where the vector potential at point o is a function of the position of current element

Electrically Short Antennas (Cont’d. . ) We have yet to consider time dependence, so: Where Jds is the retarded phasor quantity: k = β = 2π/λ

Electrically Short Antennas (Cont’d. . ) Using this current density, the phasor form is: This is what we called as the time harmonic equation for the retarded vector magnetic potential. In phasor notation, the vector magnetic potential is related to the magnetic flux density by :

Electrically Short Antennas (Cont’d. . ) From there, we could find H in free space : Because the radiation is propagating radially away from the source, it is then a simple matter to find E, where: Finally, the time averaged power radiated is:

Electrically Short Antennas (Cont’d. . ) Hertzian Dipole Suppose that a short line of current, It’s placed along the z axis as shown.

Electrically Short Antennas (Cont’d. . ) Here, the phasor current is: To maintain constant current over its entire length, imagine a pair of plates at the ends of the line that can store charge. The stored charge at the ends resembles an electric dipole, and the short line of oscillating current is then ‘Hertzian Dipole’. For Is in the +az direction through a cross sectional S, the current density at the source seen by the observation point:

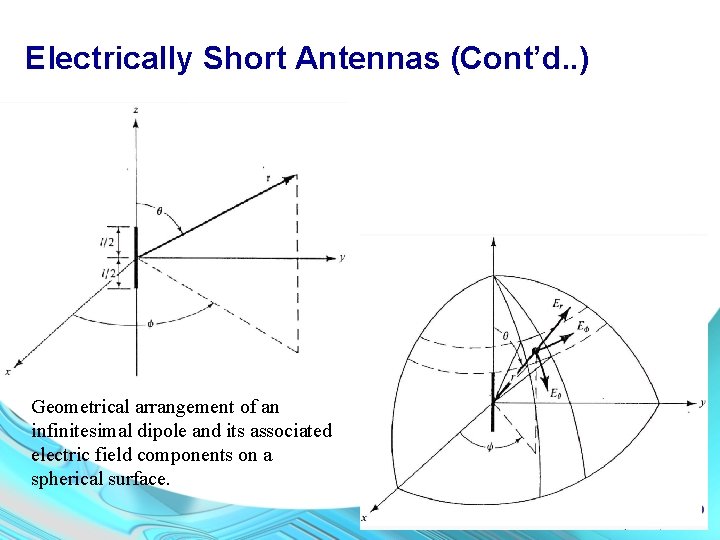
Electrically Short Antennas (Cont’d. . ) Geometrical arrangement of an infinitesimal dipole and its associated electric field components on a spherical surface.

Electrically Short Antennas (Cont’d. . ) A differential volume of this element, So, Therefore, With assumption that the Hertzian dipole is very short, integrate to get A 0 S :

Electrically Short Antennas (Cont’d. . ) The unit vector az can be converted to its equivalent spherical coordinates, so that: It is now a relatively straightforward matter to find B 0 S and then, Regroup to get:

Electrically Short Antennas (Cont’d. . ) The second terms drops off with increasing radius much faster than the first term, where for far field condition: Therefore, Meanwhile, the far field value of E field :

Electrically Short Antennas (Cont’d. . ) The time averaged power density at observation point is: The term in brackets is the max power density. The sin 2θ term is the normalized radiation intensity Pn(θ) plotted as :

Electrically Short Antennas (Cont’d. . ) The normalized radiation intensity can be used to find the pattern solid angle, The directivity is then: The total power radiated by a Hertzian dipole:

Electrically Short Antennas (Cont’d. . ) Also Rrad as: For Hertzian dipole, where l<<λ, Rrad will be very small and the antenna will not efficiently radiate power. Larger dipole antennas, have much higher Rrad and thus more efficient.

Example 3 Suppose a Hertzian dipole antenna is 1 cm long and is excited by a 10 m. A amplitude current source at 100 MHz. What is the maximum power density radiated by this antenna at a 1 km distance? What is the antenna’s radiation resistance? 56

Solution to Example 3 We should calculate the wavelength, The max. power radiated is: The antenna radiation resistance :

Electrically Short Antennas (Cont’d. . ) Small Loop Antenna A small loop of current located in the xy plane centered at the origin small loop antenna or magnetic dipole.

Electrically Short Antennas (Cont’d. . ) Substitute, Giving us, Assume that a<<λ and A 0 s is in far field. It’s discovered that, Where, and thus,

Electrically Short Antennas (Cont’d. . ) The power density vector : Where, Since the normalized power function is the same as Hertzian dipole, Ωp=8π/3, Dmax = 1. 5

Electrically Short Antennas (Cont’d. . ) Calculation of Prad and Rrad yields Try this!! The fields for the small loop antenna is similar to Hertzian dipole. It’s the dual of Hertzian (electric) dipole magnetic dipole. The equations also valid for multi turn loop, as long as the loop is small compared to wavelength. For N circular loop, S=Nπa 2 and for square coil N loops, with each side length b, S=Nb 2

4. 3 Dipole Antennas A drawback to Hertzian dipole as a practical antenna is its small radiation resistance. A longer will have higher radiation resistance, becomes more efficient. It as an L long conductor conveniently placed along the z axis with current distribution i(z, t).

Dipole Antennas (Cont’d. . ) Assume sinusoidal current distribution on each arm, where the antenna is center-fed and the current vanishes at the end points. The distribution: Where, Division of the L long dipole into a series of infinitesimal Hertzian dipoles !!

Dipole Antennas (Cont’d. . ) For simplicity, assume phase term � =0, and make use of current distribution term with magnetic field equation for a Hertzian dipole to get :

Dipole Antennas (Cont’d. . ) For far field, the vectors r and R appear to be parallel, so that θ’=θ and R=r, where: After pulling the components that don’t change with z, use table of integrals and with application to Euler’s identity,

Dipole Antennas (Cont’d. . ) The vector E 0 S is then easily found from : The time averaged power radiated is: Where, the pattern function is given by:

Dipole Antennas (Cont’d. . ) It’s not generally equivalent to the normalized power function since F(θ) can be greater than one. Therefore, the normalized power function is: And the max time averaged power density is then :

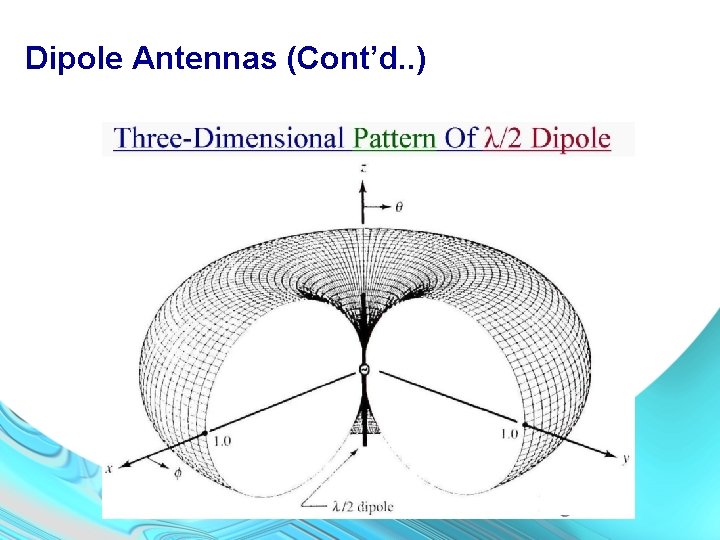
Dipole Antennas (Cont’d. . )

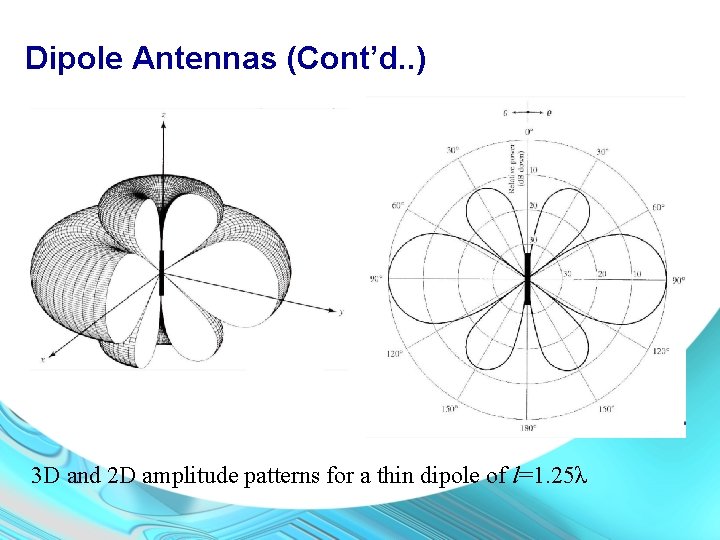
Dipole Antennas (Cont’d. . ) 3 D and 2 D amplitude patterns for a thin dipole of l=1. 25λ

Dipole Antennas (Cont’d. . ) Half Wave Dipole Antennas Because of its convenient radiation resistance, and because it’s a smallest resonant dipole antenna, the half wavelength dipole antenna merits special attention. With k. L/2 = π/2, With the F(θ) is 1, the maximum power density is:

Dipole Antennas (Cont’d. . ) Therefore, the normalized power density is: The current distribution and normalized radiation pattern for a half wave dipole antenna.

Dipole Antennas (Cont’d. . )

Dipole Antennas (Cont’d. . ) For half wave dipole… and with L = λ/2 Try this!! We can then find the directivity as : Which is slightly higher than the directivity of Hertzian dipole, the radiation resistance is given by: Leads to:

Dipole Antennas (Cont’d. . ) This radiation resistance much higher than of Hertzian dipole, where it radiates more efficiently easier to construct an impedance matching network for this antenna impedance. This antenna impedance also contains a reactive components, Xant, where for a λ/2 dipole antenna it is equal to 42. 5Ω. Therefore, total impedance by neglecting Rdiss. For impedance matching, need to make reactance zero (in resonant condition). So, it can be achieved by making the antenna slightly shorter (reduced in length until reactance vanishes).

Example 4 Find the efficiency and maximum power gain of a λ/2 dipole antenna constructed with AWG#20 (0. 406 mm radius) copper wire operating at 1. 0 GHz. Compare your result with a 3 mm length dipole antenna (Hertzian Dipole) if the center of this antenna is driven with a 1. 0 GHz sinusoidal current. 75

Solution to Example 4 We first find the skin depth of copper at 1. 0 GHz, This is much smaller than the wire radius, so the wire area over which current is conducted by: At 1 GHz, the wavelength is 0. 3 m and the λ/2 is 0. 15 m long. The ohmic resistance is then:

Solution to Example 4 (Cont’d. . ) Since the radiation resistance for half wave dipole is 73. 2Ω, we have : A gain of: Meanwhile for Hertzian Dipole, the ohmic resistance of the small dipole is :

Solution to Example 4 (Cont’d. . ) To find the radiation resistance, with value of wavelength is 0. 3 m, thus : Therefore, its efficiency and gain: Thus, the half wave dipole is clearly more efficient with a higher gain than the short dipole.

4. 4 Monopole Antennas Consider the construction of half wave dipole for an AM radio station broadcasting at 1 MHz. At this f, the wavelength is 300 m long and the half wave dipole antenna must be 150 m tall. We can cut this in half, by employing image theory to build a quarter wave monopole antenna that is only 75 m tall!!

Monopole Antennas (Cont’d. . ) Consider pair of charges, +Q and –Q (as electric dipole), where the dashed line shows the location of zero potential surface. If we slide a conductive plane over the zero potential surface, the field lines in the upper half plane are unchanged.

Monopole Antennas (Cont’d. . ) Note that the charge can be in any distribution (point charge, line charge, surface or volume charge) and the image charge is a mirror image of opposite polarity. A monopole antenna is excited by a current source at its base. By image theory, the current in the image will be the same with the current in actual monopole. The pair of monopole resembles a dipole antenna. A monopole antenna placed over a conductive plane and half the length of a corresponding dipole antenna will have identical field patterns in the upper half plane.

Monopole Antennas (Cont’d. . ) For the upper half plane (00< θ<900), the time averaged power, max power density and normalized power density for the quarter wave monopole is the same with half wave dipole. But the pattern solid angle is different.

Monopole Antennas (Cont’d. . ) Since the normalized power density is zero for (900< θ<1800), the pattern solid angle: Integrate over all space will be half value of Ωp for half wave dipole. So, for quarter wave monopole, See that the radiation resistance is halved, and the antenna impedance :

Summary of Key Antenna Parameters

Antenna End