Chapter 2 Parity checks Modular arithmetic Weighted codes

Chapter 2 Parity checks Modular arithmetic Weighted codes

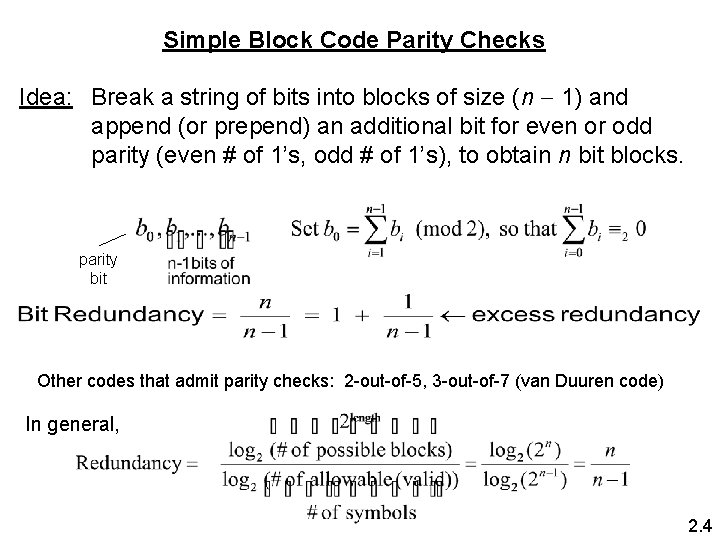
Simple Block Code Parity Checks Idea: Break a string of bits into blocks of size (n 1) and append (or prepend) an additional bit for even or odd parity (even # of 1’s, odd # of 1’s), to obtain n bit blocks. parity bit Other codes that admit parity checks: 2 -out-of-5, 3 -out-of-7 (van Duuren code) In general, 2. 4

Error Probabilities Assume independent error probability p for each bit. The probability of no error = (1 – p)n. The probability of one error = np(1 – p)n-1. i In general 1 √ … √ n √ … √

Burst Code Parity Checks Assume noise comes in “bursts” of length ≤ L, and is otherwise independently distributed. Instead of computing a parity check over contiguous sequences of bit positions, use a “checksum” over words of length L. physical noise b 1 … b. L+1 … b 2 L . . . c 1 … c. L checksum 2. 6

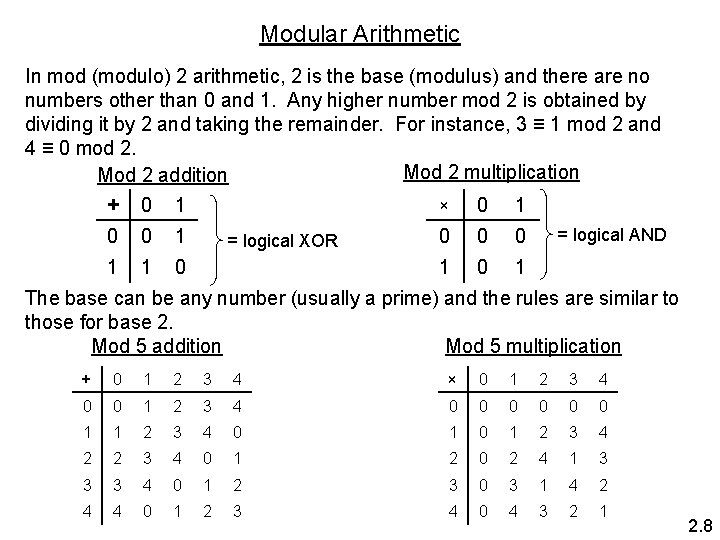
Modular Arithmetic In mod (modulo) 2 arithmetic, 2 is the base (modulus) and there are no numbers other than 0 and 1. Any higher number mod 2 is obtained by dividing it by 2 and taking the remainder. For instance, 3 ≡ 1 mod 2 and 4 ≡ 0 mod 2. Mod 2 multiplication Mod 2 addition × + 0 1 0 0 1 1 1 0 = logical XOR 0 0 0 1 = logical AND The base can be any number (usually a prime) and the rules are similar to those for base 2. Mod 5 addition Mod 5 multiplication + 0 1 2 3 4 × 0 1 2 3 4 0 0 0 0 1 1 2 3 4 0 1 2 3 4 2 2 3 4 0 1 2 0 2 4 1 3 3 3 4 0 1 2 3 0 3 1 4 2 4 4 0 1 2 3 4 0 4 3 2 1 2. 8

Rules for Modular arithmetic Fact: If a ≡m a′ and b ≡m b′, then a + b ≡m a′ + b′ and a ∙ b ≡m a′ ∙ b′. Proof: a ≡m a′ and b ≡m b′ means that a = a′ + im and b = b′ + jm, so a + b = a′ + b′ + (i + j)m and a ∙ b = a′ ∙ b′ + a′jm + b′im + ijm 2. QED Multiplicative inverses may not exist for some numbers. Example: 2 × 5 ≡ 0 mod 10. Does 2 have a multiplicative inverse? Suppose it does, then 2 × 2− 1 ≡ 1 mod 10. However, multiplying both sides by 5 yields 0 ≡ 5 mod 10, which is false. Note: If the modulus is a prime, p, then numbers not congruent to p can’t multiply together to be congruent to p, so you don’t have the problem in the above example. Here is a proof that multiplicative inverses (for nonzero) numbers always exist in a prime modulus, p: Let q , 0 < q < p, then GCD(p, q) = 1. (They are relatively prime). By the Euclidean Algorithm, we can always 2. 8 find k, l such that kp + lq = 1, lq ≡ 1 mod p l = q− 1.

Weighted Codes Deals with transcription errors (i. e. human non-binary error): Example: Assign numerical values 1 … 37 to the symbols consisting of letters, digits, and a space. Take a message of length less than 37 and weight each symbol therein according to its position in the message, appending a final check symbol s 1 chosen so the weighted sum is congruent to zero: For n < 37, sn… … s 1 transposing adjacent digits [e. g. 67 → 76]: ksk + (k+1)sk+1 becomes (k+1)sk + ksk+1 whose difference is sk+1 − sk ≢ 0 (mod 37) repeating an adjacent digit [e. g. 667 → 677]: difference is ksk − ksk+1 = k(sk − sk+1) ≢ 0 provided 0 < k < 37 and sk ≠ sk+1

ISBN Numbers 10 digit weighted code (mod 11) where X stands for ten in the check (last) digit 10 9 8 7 6 5 4 3 2 1 0 1 3 2 1 2 5 7 1 4 message highest weight: w sum → w sum of sums → ↓ x → w+x ↓ → ↓ y → w+x+y z → w+x+y+z 2 w + x ↓ → ↓ check digit (weight 1): w 3 w + 2 x + y ↓ → 4 w + 3 x + 2 y + z 2. 9