Chapter 2 Operational Amplifier Circuits 2 1 Bias

Chapter 2 Operational Amplifier Circuits

2. 1 Bias Circuit Suitable for IC Design w The bias circuits used to bias discrete BJT need large number of resistors as well as large coupling and bypass capacitors w Biasing in integrated circuit design is based on the use of constant current sources w On an IC chip with a number of amplifier stages a constant dc current is generated at one location and is then reproduced at various other locations of biasing the various amplifier stages

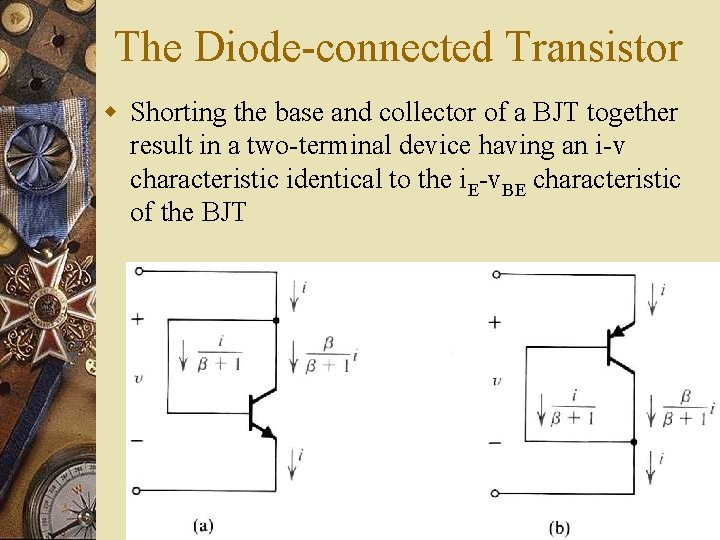
The Diode connected Transistor w Shorting the base and collector of a BJT together result in a two terminal device having an i v characteristic identical to the i. E v. BE characteristic of the BJT

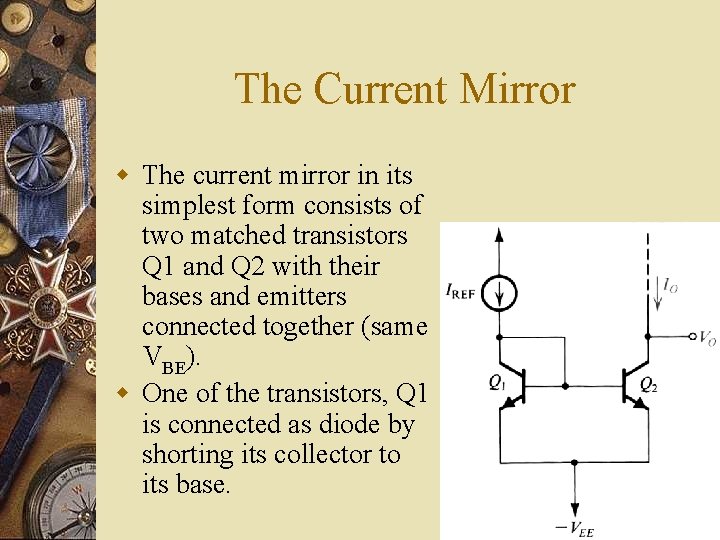
The Current Mirror w The current mirror in its simplest form consists of two matched transistors Q 1 and Q 2 with their bases and emitters connected together (same VBE). w One of the transistors, Q 1 is connected as diode by shorting its collector to its base.

Derivation w Since Q 2 is identical to Q 1, IE 2 = IE 1 = Iref. Therefore, Io is approximately equal to Iref (as long as Q 2 is maintained in the active region. ) [ic=Is e. VBE/VT (1+VCE/VA)]

Effect of Finite w IREF = (2+ ) / (1+ ) IE and w I 0 = / (1+ ) IE w Therefore I 0 / IREF = /( +2) = 1 / (1+2/ ) which approaches unity for >>1. w = 100 results in 2% error.

Practical Side w Another factor that makes I 0 unequal to IREF is the linear dependence of the collector current of Q 2 , which is I 0, on the collector voltage of Q 2. w In fact, even if we ignore the effect of finite and assume that Q 1 and Q 2 are perfectly matched, the current I 0 will be equal to IREF only when the voltage at the collector of Q 2 is equal to the base voltage. w As the collector voltage is increased, I 0 increases. The dependence of I 0 on V 0 is determined by r 0 of Q 2.

2. 2 The Widlar Current Source w Simple current source w IREF, determined by a resistor R connected to the positive power supply VCC. The current IREF is given by w IREF = (VCC – VBE)/R w The circuit will operate as a constant current source as long as Q 2 remains in the active region that is, for V 0 VBE. The output resistance of this current source is r 0 of Q 2.

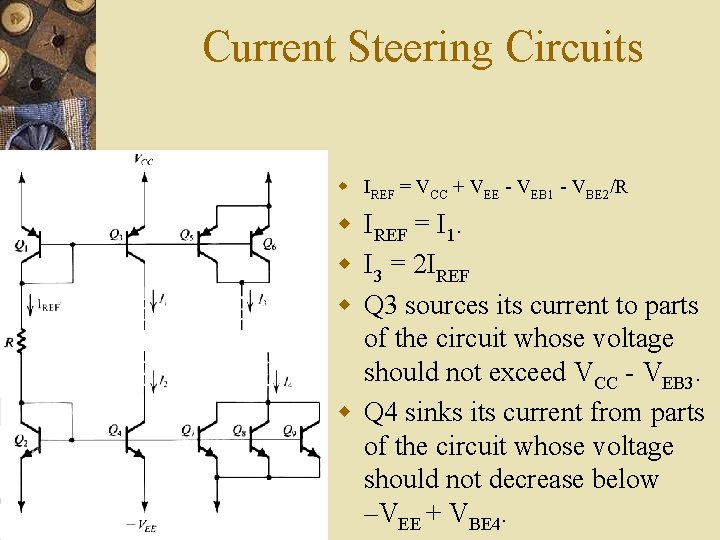
Current Steering Circuits w IREF = VCC + VEE VEB 1 VBE 2/R w IREF = I 1. w I 3 = 2 IREF w Q 3 sources its current to parts of the circuit whose voltage should not exceed VCC VEB 3. w Q 4 sinks its current from parts of the circuit whose voltage should not decrease below –VEE + VBE 4.

Improved Current Source Circuit w I 0/IREF 1/(1+2/ 2) w which means that the error due to finite has been reduced from 2/ to 2/ 2, a tremendous improvement w An alternative mirror circuit that achieves both base current compensation and increased output resistance is the Wilson mirror

The Widlar Current Source w VBE 1 = VT ln (IREF/IS) w VBE 2 = VT ln (I 0/IS), w VBE 1 VBE 2 = VT ln (IREF/I 0) w From the circuit, w VBE 1 = VBE 2 + I 0 RE w and so, I 0 RE = VT ln (IREF/IO)

The Widlar Current Source w Widlar circuit allows generation of a small constant current using relatively small resistors which results in considerable savings in chip area. Another characteristic of a Widlar circuit is that its output resistance is high due to the presence of emitter resistance RE

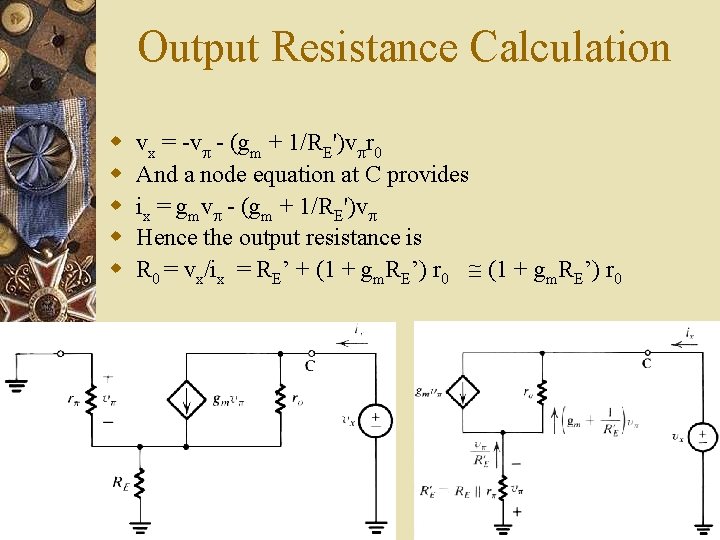
Output Resistance Calculation w w w vx = v (gm + 1/RE')v r 0 And a node equation at C provides ix = gmv (gm + 1/RE')v Hence the output resistance is R 0 = vx/ix = RE’ + (1 + gm. RE’) r 0

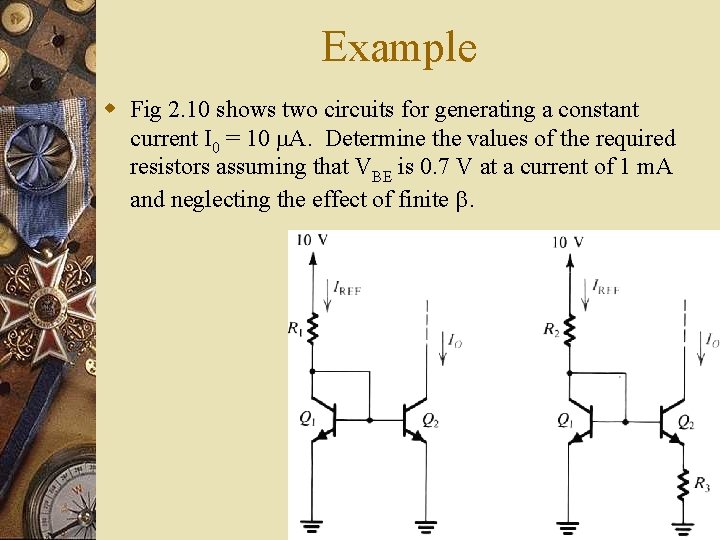
Example w Fig 2. 10 shows two circuits for generating a constant current I 0 = 10 A. Determine the values of the required resistors assuming that VBE is 0. 7 V at a current of 1 m. A and neglecting the effect of finite .

2. 3 The Differential Amplifier w The output of a differential amplifier is proportional to the difference between the two input voltages

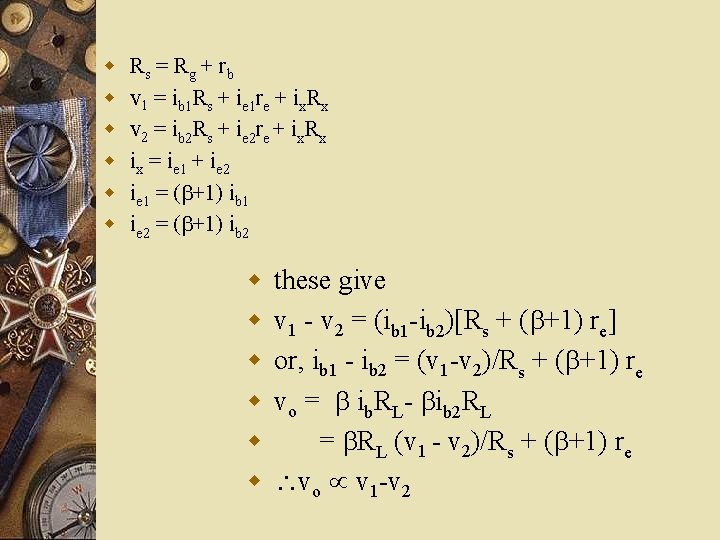
w w w Rs = R g + rb v 1 = ib 1 Rs + ie 1 re + ix. Rx v 2 = ib 2 Rs + ie 2 re + ix. Rx ix = ie 1 + ie 2 ie 1 = ( +1) ib 1 ie 2 = ( +1) ib 2 w w w these give v 1 v 2 = (ib 1 ib 2)[Rs + ( +1) re] or, ib 1 ib 2 = (v 1 v 2)/Rs + ( +1) re vo = ib. RL ib 2 RL = RL (v 1 v 2)/Rs + ( +1) re vo v 1 v 2

Small Signal Analysis w Assume two perfectly matched transistors Q 1 and Q 2 (have identical values of , re etc. ) connected in differential amplifier configuration. Consider a small signal vi 1 applied to input 1, and input 2 grounded. Assuming the constant current source to be ideal, it presents an infinite impedance (open circuit) to an ac signal [since the current has to be constant ac signal cannot flow through it], so its presence need not be considered.

Small Signal Analysis w Take re 1 = re 2, then vbe 1 = vbe 2 = vi 1/2 [(vi 1/2 re) re] w Vbe 1 is in phase with, and one half the magnitude of vi 1. vbe 2 is out of phase with vi 1. The output voltage vo 1 is amplified and inverted version of the input vi 1 [common emitter amplifier action]. w There will also be an output voltage at the collector of Q 2 (vo 2) and it is out of phase with ve 2 ( out of phase with vo 1). However, the magnitude of vo 2 is equal to that of vo 1, because the transistors Q 1 and Q 2 are matched.

Graphical Illustration w By superposition principle, it follows that, if both vi 1 and vi 2 were present at the same time, the resulting outputs would be exactly twice the level w Note that the voltage at each collector will be exactly 0, if the inputs are driven by in phase voltages of equal magnitude. In such a case, the input differential voltage as well as the output differential voltage will also be 0

Derivation in terms of circuit parameters w With Q 2 base grounded, the resulting circuit is shown in figure. Neglecting ro at the collector of Q 1, vo 1/vbe 1 RC/re w Therefore, the voltage gain, vo 1/vi 1= Rc/2 re w Hence, (vo 1 vo 2)/(vi 1 vi 2) = RC/re and vo 1/(vi 1 vi 2) = RC/2 re

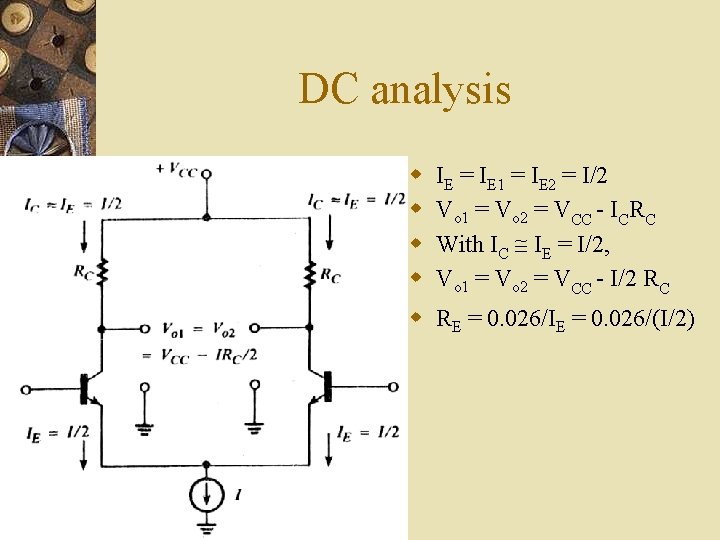
DC analysis w w IE = IE 1 = IE 2 = I/2 Vo 1 = Vo 2 = VCC ICRC With IC IE = I/2, Vo 1 = Vo 2 = VCC I/2 RC w RE = 0. 026/IE = 0. 026/(I/2)

2. 4 Active Loads w Transistors occupy much less silicon area than resistors, so many BJT ICs use BJT loads in place of the resistive loads, RC. In such circuits, the BJT load transistor is usually connected as a constant current source and thus presents the amplifier transistor with a very high resistance load (the output resistance of the current source). Thus amplifiers that utilize active loads can achieve higher voltage gains than those with passive (resistive) loads

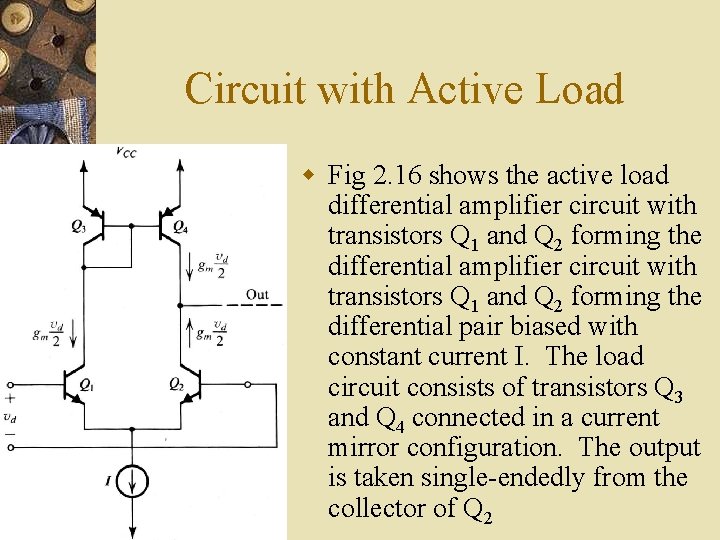
Circuit with Active Load w Fig 2. 16 shows the active load differential amplifier circuit with transistors Q 1 and Q 2 forming the differential pair biased with constant current I. The load circuit consists of transistors Q 3 and Q 4 connected in a current mirror configuration. The output is taken single endedly from the collector of Q 2

w Consider the first case when no input signal is applied (that is the two input terminals are grounded). The current I splits equally between Q 1 and Q 2. Thus Q 1 draws a current approximately equal to I/2 from the diode connected transistor Q 3. Assuming >>1, the mirror supplies an equal current I/2 through the collector of Q 4. Since this current is equal to that through the collector of Q 2, no output current flows through the output terminal. [In practical circuits, the dc quiescent voltage at the output terminal is determined by the subsequent amplifier stage]

w Next consider a differential signal vd is applied at the input. Current signals gm(vd/2) will result in the collector of Q 1 and Q 2 with polarities indicated in figure. The current mirror reproduces the current signal gm(vd/2) through the collector of Q 4. Thus at the output node we have two current signals that add together to produce a total current signal of gmvd. Now if the resistance presented by the subsequent amplifier stage is very large, the voltage signal at the output terminal will be determined by the total signal current and the total resistance between the output terminal and ground Ro; that is w vo = gmvd Ro w Ro = parallel equivalence of the output resistance of Q 2 and the output resistance of Q 4.

w Since Q 2 is operating in common emitter configuration, its output resistance will be equal to r 02. Also, the output resistance of basic current mirror is equal to ro of Q 4, that is ro 4. w Ro = ro 2||ro 4 = ro/2 w and vo = gmvd(ro/2) w voltage gain vo/vd = gmro/2 w Substituting gm = IC/VT and ro = VA/IC, where IC = I/2, w gmro = VA/VT = constant for given transistor. w Typically VA =100 v, leading to gmro = 4000 and a stage voltage gain of about 2000. w Without the current mirror (that is, using only a simple current source) the voltage gain would be half the value found above

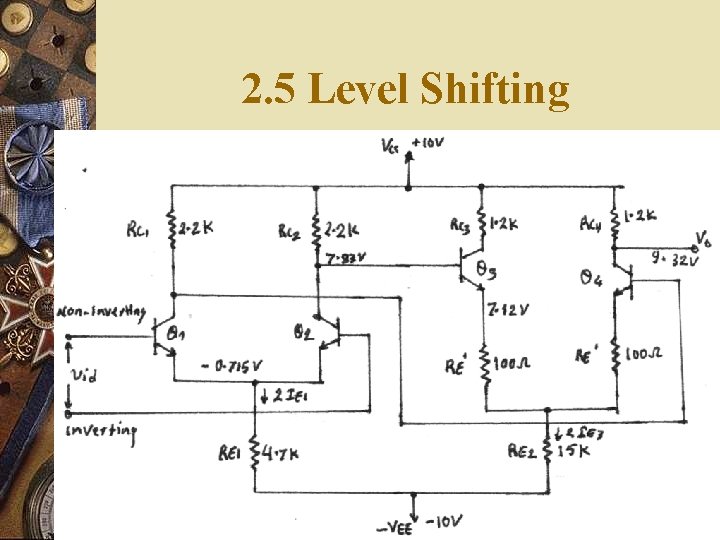
2. 5 Level Shifting

Circuit Calculations w w w w w 2 IE 1 = (VEE VBE)/RE 1 IE 1 = 0. 988 m. A IC 1 = IC 2 VC 1 = VC 2 = VCC IC 1 RC 1 = 7. 83 V 100 * IE 3 + 15 k * 2 IE 3 = 17. 12 IE 3 = 0. 569 m. A = IE 4 VC 3 = VC 4 = VCC RC 3 IC 3 = 9. 32 V VCE 1 = VCE 2 = 8. 545 V VCE 3 = VCE 4 = 2. 2 V

Findings w Because of direct coupling, the dc levels at the emitters rises from stage to stage. This increase in dc level tends to shift the operating point of the succeeding stages and, therefore, limits the output voltage swing and may even distort the output signal. w The voltage at the output terminal of the second stage is well above ground. This dc level is undesirable because it tends to limit the p to p output voltage swing without distortion and also contributes to the error in the dc output signal. w Therefore a final stage should be included to shift the output dc level at the second stage down to zero volts. Such a stage is referred to as a level translator of shifter.

Level Shifting Circuits w There a variety of level shifting circuits. An emitter follower with a voltage divider is the simplest among them. The output of the second differential stage is input to Q 5. Thus a positive 9. 32 V at the output terminal (VC 4) of the second stage can produce zero volts at the junction of R 1 and R 2 with proper selection of components.

Better Level Shifting Circuits w RE = 0. 7/3 m. A = 233. 3 (use 270 ) w Taking I 2 = IE 6 w R 2 = (VEE 1. 4)/IE 6 =2. 87 k (use 2. 7 k ) w Take VBE 5 = 0. 7 V which gives w VE 5 = 9. 32 0. 7 = 8. 62 V w IE 5 = IC 6 3 m. A; VC 6 = 0 V w R = 8. 62/3 m. A = 2. 87 k (use 3 k potentiometer)

Better Level Shifting Circuits w I 2 = (VEE 0. 7)/R 2 w R 2 = 9. 3/3 m. A = 3. 1 k w and R = 8. 62/3 m. A = 2. 87 k w Better results are attained by using an emitter follower with a diode constant current bias or a current mirror instead of the voltage divider.

2. 6 Output Stages w The purpose of the output stage is to provide the amplifier with a low output resistance. In addition, the output stage should be able to supply relatively large load currents without dissipating a large amount of power in the IC.

Circuit Analysis of an operational amplifier w Q 1 and Q 2 form the input differential stage. The signal inputs are grounded for the purpose of dc analysis and we wish to verify that the output is zero V under those conditions. The 50 resistor in the emitters of Q 1 and Q 2 serve to increase the amplifier’s input impedance and to make the stage less sensitive to variations in re. Q 3 and Q 4 form an unbalanced differential stage that provides additional voltage gain. Q 5 performs the level shifting function. Q 6 is an emitter follower whose output is the output of the operational amplifier. Q 7 and Q 8 are constant current sources that bias the two differential stages. These sources share a common voltage divider across the transistor bases.

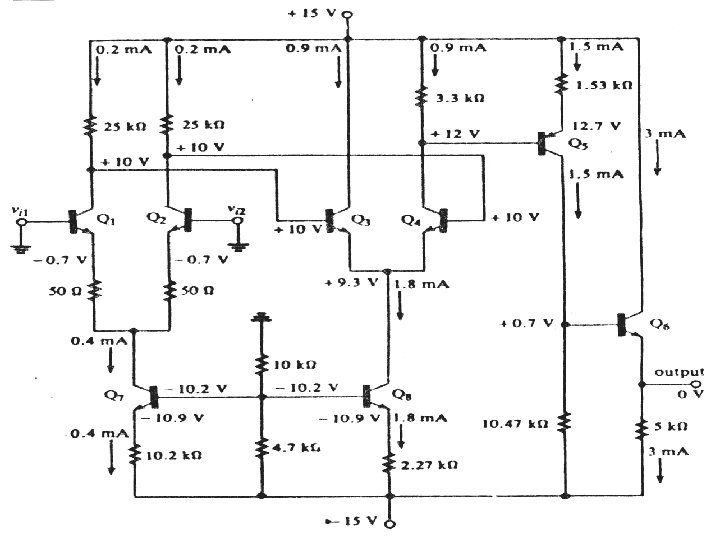
DC analysis w The voltage divider across the base of Q 7 sets the base voltage to w VB 7 = [10 k /(10 k + 4. 7 k )]( 15 V) = 10. 2 V w Therefore, the emitter voltage of Q 7 is VB 7 0. 7 = 10. 9 V, and the emitter current is w IE 7 = (|VEE| |VE 7|)/RE 7 = (15 10. 9)V/10. 2 k = 0. 4 m. A

DC Analysis Contd. w Assuming matched conditions, this current divides equally between Q 1 and Q 2, and, since IC 1 = IC 2 IE 2 = (0. 4 m. A)/2 = 0. 2 m. A, the collector voltages at Q 1 and Q 2 are VC 1 = VC 2 = VCC ICRC = 15 (0. 2 m. A)(25 k ) = 10 V. Since the bases of Q 1 and Q 2 are grounded, their emitters are at approximately 0 0. 7 V = 0. 7 V, and the small drop across each 50 resistor [(50 ) x (0. 2 m. A) = 0. 01 V] sets the collector of Q 7 at about the same voltage ( 0. 71 V).

DC Analysis Contd 2. w We can now analyze the bias of the second differential stage. Since VB 8 = VB 7 = 10. 2 V, the emitter of Q 8 is at VE 8 = VB 8 – 0. 7 = 10. 9 V. Then w IE 8 = (|VEE| |VE 8|)/RE 8 = (15 10. 9)/2. 27 k = 1. 8 m. A w The 1. 8 m. A divides equally between Q 3 and Q 4, so the collector voltage of Q 4 is VC 4 = VCC ICRC = 15 (0. 9 m. A)(3. 3 k ) = 12 V. Since the bases of Q 3 and Q 4 are directly coupled to the collectors of Q 1 and Q 2, the base voltages are VB 3 = VB 4 =10 V. The emitter voltages are VE 3 = VE 4 = 10 0. 7 = 9. 3 V.

DC Analysis Contd 3. w The base of the level shifting PNP transistor, Q 5, is direct coupled to Q 4, so VB 5 = 12 V. Therefore, Q 5 has emitter voltage VE 5 = VB 5 + 0. 7 = 12. 7 V. The emitter current in Q 5 is w IE 5 = (VCC VE 5)/RE 5 = (15 12. 7) / 1. 53 = 1. 5 m. A w Since IC 5 IE 5, the collector of Q 5 is at VC 5 = (IC 5)(10. 47 k ) VEE = (1. 5 m. A)(10. 47 k ) – 15 = +0. 7 V. w Q 5 accomplishes level shifting because its collector can go both positive and negative. w Since the base of the output transistor, Q 6, is at 0. 7 V, its emitter is at 0 V, and we see that the amplifier output is 0 V. The bias current in Q 6 is (0 – VEE) / 5 = 15 / 5 = 3 m. A.