Chapter 2 Number Systems Operations and Code DECIMAL

Chapter 2 Number Systems, Operations and Code

DECIMAL NUMBER • The decimal number composed of 10 symbols. • Ex: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; these symbols as digits of the numbers. The decimal number also called the base 10 number because it has ten digits.

Positional values MSB = Most Significant Bit LSB = Least Significant Bit

Express the decimal number below as a sum of the value of each digit a) 57 b) 387. 31 c) 13. 542 EXERCISE 1

BINARY NUMBER • Almost every digital system uses the binary (base 2) number system as the basic number system of its operations. • In the binary number only have two possible digit values, 0 and 1. Each binary digit has its own value or weight expressed as a power of 2.

Binary Weight 28 27 26 25 24 23 22 21 20 . 2 -1 2 -2 256 128 64 32 16 8 4 2 1 Decimal point 0. 5 0. 25 The left most bit is the MSB and the right most bit is LSB. The value of a bit is determined by its position in the number. In general, with n bits you can count up to a number equal to 2 n – 1. For example, with three bits (n = 3), you can count from 0 to 7. = 2 n – 1 = 23 – 1 =7

Binary to decimal conversion Example Convert the binary whole number 1101101 to decimal Weight: 26 25 24 23 22 21 20 Binary Number : 1 1 0 1 1101101 = 26 + 25 + 23 + 22 + 20 = 64 + 32 + 8 + 4 + 1 = 109

• EXERCISE Convert the binary number below to decimal a) 0. 1101 b) 1010111 c) 101011. 011

Decimal to Binary Conversion • Two ways to convert a decimal number to binary number: 1. using Sum of Weights method 2. using the repeated division by 2

Sum of Weights Method • To get the binary number for a given decimal, find the binary weights that add up to the decimal number. • Example The decimal number is 11. So you can expressed as the sum of binary weight as follows 11 = 8 + 2 + 1 or 11 = 23 + 21 + 20 Placing 1 s in appropriate weight 23 22 21 20 1 1 So, the binary number for 11 is 1011

Repeated Division by 2 Method • Another method for converting decimal integers uses repeated division by 2. • It requires repeatedly dividing the decimal number by 2 and writing down the reminder after each division until a quotient of 0 is obtained.

Example Convert decimal numbers 13 to binary 1 0 1 1 MSB 1101 LSB

Converting decimal fractions to Binary • Two ways to convert a decimal number to binary number: 1. using sum of weights method 2. using the repeated multiplication by 2

1. Using Sum of Weight Method • To get the binary number for a given fractional decimal, find the binary weights that add up to the decimal number. • Example The decimal number is 0. 625. So you can expressed as the sum of binary weight as follows 0. 625 = 0. 5 + 0. 125 or 0. 625 = 2 -1 + 2 -3 Placing 1 s in appropriate weight 2 -1 2 -2 2 -3 1 So, the binary number for 0. 625 is 0. 101 0 1

2. Using the Repeated Multiplication by 2 • Multiplying by 2 until the fractional product is zero or until the desired number of decimal places is reached. • The carry digits, or carries, generated by the multiplications produce the binary number. The first carry produced is the MSB, and the last carries is the LSB.

Example Convert decimal numbers 0. 3125 to binary Carry 0. 3125 x 2 = 0. 625 0 0. 625 x 2 = 1. 25 1 0. 25 x 2 = 0. 50 0 0. 5 x 2 = 1. 00 1 MSB 0. 0101 LSB

BINARY ADDITION The rules for binary addition are 0+0=0 Sum = 0, carry = 0 0+1=1 Sum = 1, carry = 0 1+0=1 Sum = 1, carry = 0 1+1=0 Sum = 0, carry = 1 When an input carry = 1 due to a previous result, the rules are 1 + 0 = 01 Sum = 1, carry = 0 1 + 0 + 1 = 10 Sum = 0, carry = 1 1 + 0 = 10 Sum = 0, carry = 1 1 + 1 = 11 Sum = 1, carry = 1

EXERCISE 2 Add the following binary numbers a) 11 + 11 b)100 + 10 c) 111 + 11 d)110 + 100

BINARY SUBTRACTION • The 4 basic rules for subtracting bits are follows: 0– 0=0 1– 1=0 1– 0=1 10 – 1 = 1 with a borrow of 1 REMEMBER 10 – 1 = 1, not 9

• EXERCISE 3 a) b) c) d) 11 -01 011 -101 1001 -0111 10101 -00111

BINARY MULTIPLICATION • The four basic rules for multiplying bits are as follows: 0 x 0=0 0 x 1=0 1 x 0=0 1 x 1=1 BINARY DIVISON • Division in binary follows the same procedure as division in decimal.

• • a) 1101 x 11 b) 101 x 101 c) 1110 ÷ 10 d) 10010 ÷ 110 EXERCISE 4

1’s and 2’s Complement of Binary Numbers • The 1’s complement of a binary number is found by changing all 1 s to 0 s and all 0 s to 1 s.

2’s Complement The 2’s complement of binary is found by adding 1 to the LSB on the 1’s complement. 2’s complement = (1’s complement) + 1 Example Find the 2’s complement of 10110010 1 1 0 0 1 1 0 1 + 1 0 0 1 1 1 0 Binary Number 1’s complement Add 1 2’s complement

• Find 1’s complement and 2’s complement for binary number below • a) 10101011 • b) 10001101 • c) 00010111 EXERCISE 5

SIGNED NUMBER • Sign bit The left most bit in a signed binary number is the sign bit, which tell you whether then number is positive or negative. 0 sign bit indicates a positive number 1 sign bit indicates a negative number. • Sign Magnitude Form • When a signed binary number is represented in sign magnitude, the left most bit is the sign bit and the remaining bits are the magnitude bits. The magnitude bits are in true (uncomplemented) binary for both positive and negative numbers.

Example + 25 = 0 0011001 Magnitude bit Signed bit -25 = 1 0011001 Magnitude bit Signed bit In signed magnitude form, a negative number has same magnitude bits as corresponding positive number but the sign bit is a 1 rather than zero

1’s Complement Form In the 1’s complement form, negative number is the 1’s complement of corresponding positive number. Example Using 8 -bits, decimal number for -25 is expressed as 1’s complement of +25 = 00011001 So, in 1’s complement form -25 = 1’s complement of +25 = 11100110

2’s Complement Form In the 2’s complement form, negative number is the 2’s complement of corresponding positive number. Example Using 8 -bits, decimal number for -25 is expressed as 2’s complement of +25 = 00011001 So, in 2’s complement form -25 = 2’s complement of +25 = 11100111

EXERCISE 6 Express the decimal number -39 as an 8 bit number in the sign magnitude, 1’s compliment form & 2’s compliment form

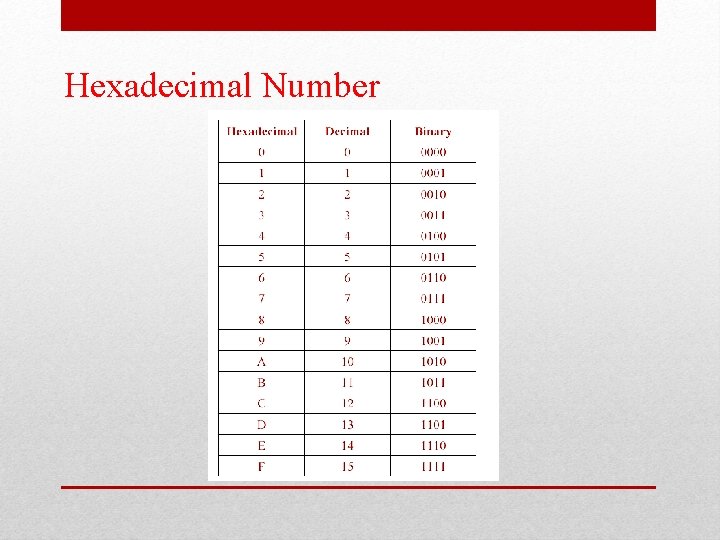
Hexadecimal Number

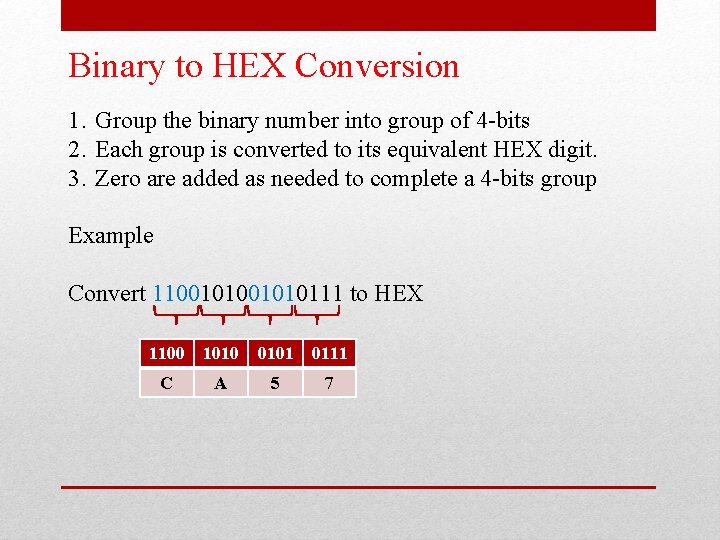
Binary to HEX Conversion 1. Group the binary number into group of 4 -bits 2. Each group is converted to its equivalent HEX digit. 3. Zero are added as needed to complete a 4 -bits group Example Convert 11001010111 to HEX 1100 1010 C A 0101 0111 5 7

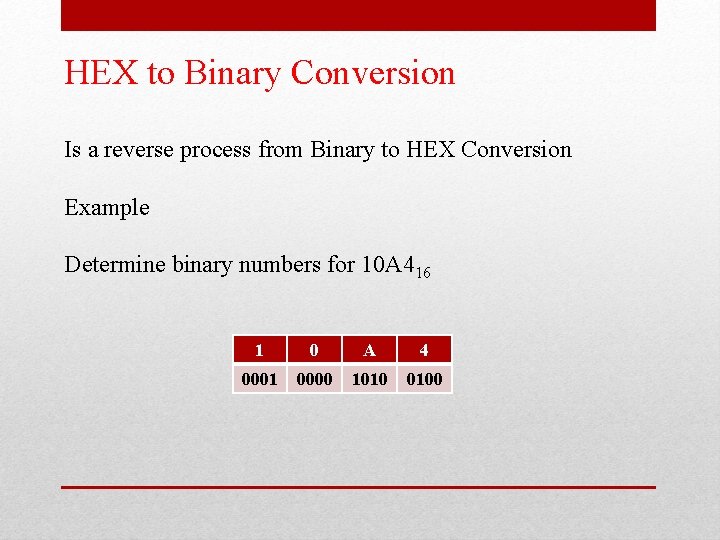
HEX to Binary Conversion Is a reverse process from Binary to HEX Conversion Example Determine binary numbers for 10 A 416 1 0 A 4 0001 0000 1010 0100

HEX to Decimal Conversion Multiply the decimal value of each hex digit by its weight and then take the sum of these product. Example Convert 1 C 16 to decimal 1 C 16 = (1 x 16) + (C x 1) = (1 x 16) + (12 x 1) = 2810 C 16 = 1210 161 160 1 C

Decimal to HEX Conversion Example • Convert 65010 to HEX Reminder Stop when whole number quotient is zero A 8 2 MSB 28 A LSB

a) b) c) d) Convert 11110101001001012 to HEX Convert F 85 C 16 to binary Convert 6 A 16 to decimal Convert 67410 to HEX EXERCISE 7

Binary Coded Decimal (BCD) Each decimal digit represented by 4 -bits binary coded. Designation 8421 indicate the binary weight of 4 -bits. (23, 22, 21, 20) Decimal Digit 0 1 2 3 4 5 BCD 0000 0001 0010 0011 0100 0101 Invalid Code The six code combination are not in used 1010, 1011, 1100, 1101, 1110, 1111 6 7 0110 0111 8 9 1000 1001

Convert each of the following decimal number to BCD a) 35 b) 170 Convert each of the following BCD codes to decimal a) 10000110 EXERCISE 8

BCD Addition • BCD is numerical code and can be used in arithmetic operation. • Step: 1. Add the two BCD numbers, using the rules for binary addition 2. If a 4 bit sum is equal to or less than 9, it is a valid BCD number 3. If a 4 bit sum is greater than 9, or if a carry out of the 4 bit is generated, it is an invalid result. Add 6(0110) to the for bit sum in order to skip the six invalid states and return the code to 8421. If a carry results when 6 is added, simply add the carry to the next 4 bit group.

a) 0011 + 0100 b) 1001 + 0100 0011 + 0100 0111 1001 + 0100 1101 + 0110 0001 0011 1 EXAMPLE 3 Invalid BCD number (>9) Add 6(0110) Valid BCD number

Add the following BCD numbers a) 0011 + 0100 b) 1001 + 0100 c) 10000110 + 00010011 d) 01100111 + 01010011 e) 00010110 + 00010101 EXERCISE 9