Chapter 2 Number Systems Introduction A number system

Chapter 2 Number Systems

Introduction A number system is a set of symbols used to express quantities as the basis for counting, determining order, comparing amounts, performing calculations.

The Decimal Number System The decimal number system is used in our everyday life. It has values from 0 – 9. Decimal number system has a base of 10. This means that each digit in the number is multiplied by 10 raised to a power corresponding to that digit’s position.

Decimal Number System (con’t. ) (47)10 7 x 100 = 7 X 1 4 x 101 = 4 X 10

Decimal Number System (con’t. ) (4928)10 8 2 9 4 x x 100 = 101 = 102 = 103 = 8 x 1 1 x 10 9 x 100 4 x 100

The Binary Number System Binary is a number system used by digital devices like computers. In the binary system, there are only two digits, 0 and 1. The binary system is said to have a base of 2.

Binary Number System (con’t. ) (1001)2 1 0 0 1 x x 20 21 22 23 = 1 x 1 = 0 x 2 = 0 x 4 = 1 x 8

The Hexadecimal Number System Hexadecimal number system is a numeral system with a base of 16. The values are represented by 0 -9, A, B, C, D, E, F. Each hexadecimal digit represents four (4) binary bits.

The Octal Number System Octal number system is a numeral system with a base of 8. The values are represented by 0 -7. Each octal digit represents three (3) binary bits.

Conversions between Binary and Decimal Number System (10011)2 1 1 0 0 1 x x x 20 = 21 = 22 = 23 = 24 = 1 x 1 1 x 2 0 x 4 0 x 8 1 x 16 (19)10

Conversions between Binary and Decimal Number System (101001)2 1 0 0 1 x x x 20 = 21 = 22 = 23 = 24 = 25 = 1 x 1 0 x 2 0 x 4 1 x 8 0 x 16 1 x 32 (41)10

Conversions between Binary and Decimal Number System (con’t. ) (101. 011)2 1 x 2 -3 = 1 x 1/8 = 1 x 0. 125 1 x 2 -2 = 0 x 1/4 = 1 x 0. 250 0 x 2 -1 = 0 x 1/2 = 0 x 0. 500 1 x 21 = 0 x 1 0 x 22 = 1 x 2 1 x 23 = 1 x 4 =1 =0 =4 (5. 375)10

Conversions between Binary and Decimal Number System (con’t. ) (1100. 1011)2 1 1 0 0 1 1 x x x x 2 -4 = 1 x 1/8 2 -3 = 1 x 1/8 2 -2 = 0 x 1/4 2 -1 = 0 x 1/2 20 = 0 x 1 21 = 0 x 2 22 = 1 x 4 23 = 1 x 8 = 1 x 0. 0625 = 1 x 0. 125 = 0 x 0. 250 = 1 x 0. 500 =0 =0 =4 =8 (12. 6875)10

Conversions from Decimal to Binary Number Systems To convert a decimal number to its binary equivalent, we should repeatedly divide the decimal number by 2.

Conversions from Decimal to Binary Number Systems (con’t. ) (18)10 2 Use = N A R 2 2 18 0 (LSD) 9 1 4 0 2 0 1 (MSD) (10010)2

Conversions from Decimal to Binary Number Systems (con’t. ) (43)10 = 2 2 2 43 1 (LSD) 21 1 10 0 5 1 2 0 1 (MSD) (101011)2

Conversions from Decimal to Binary Number Systems (con’t. ) To convert the decimal fraction to a binary number, repeatedly multiply the decimal fraction by 2.

Conversions from Decimal to Binary Number Systems (con’t. ) (0. 375)10 0. 375 * 2 = 0. 75 * 2 = 1. 5. 50 * 2 = 1. 0 (0. 011)2 (MSD) (LSD)

Conversions from Decimal to Binary Number Systems (con’t. ) (0. 432)10 0. 432 * 2 = 0. 864 * 2 = 1. 728 * 2 = 1. 456 * 2 = 0. 912 * 2 = 1. 824 (0. 01101)2 (MSD) (LSD)

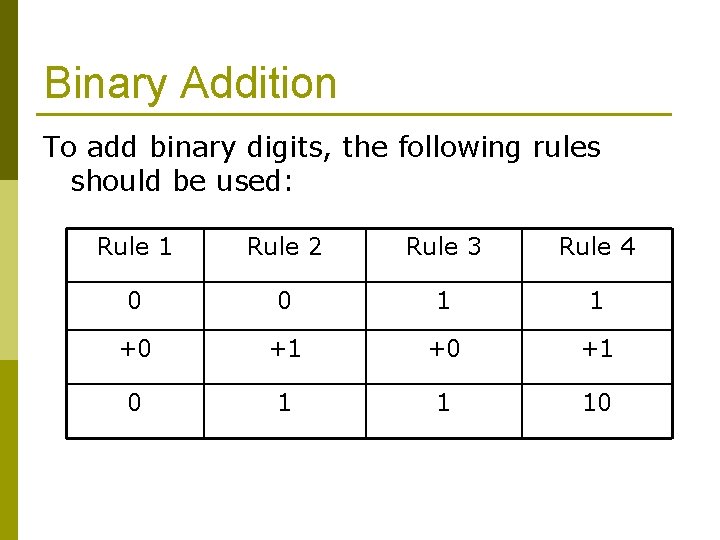
Binary Addition To add binary digits, the following rules should be used: Rule 1 Rule 2 Rule 3 Rule 4 0 0 1 1 +0 +1 0 1 1 10

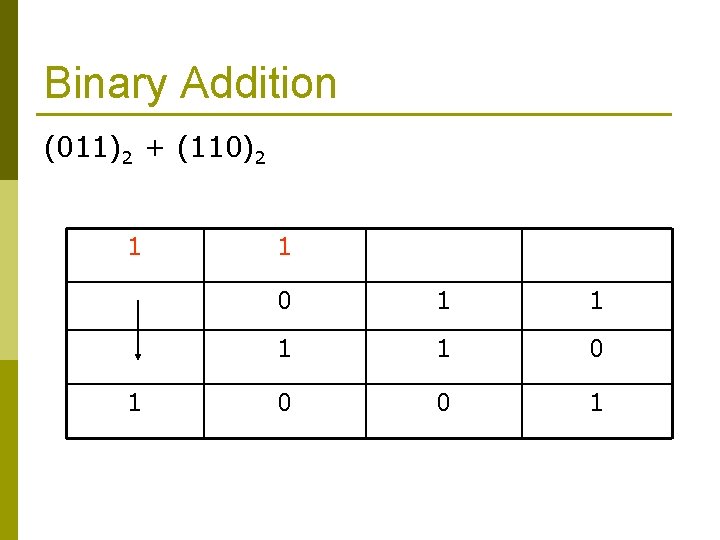
Binary Addition (011)2 + (110)2 1 1 1 0 0 0 1