Chapter 2 Motion in One Dimension 1 Kinematics

Chapter 2 Motion in One Dimension 1

Kinematics n Describe motion while ignoring the agents that caused the motion n n For now, consider motion in one dimension n n Motion represents a continual change in an object’s position Along a straight line Use the particle model n A particle is a point-like object, has mass but infinitesimal size 2

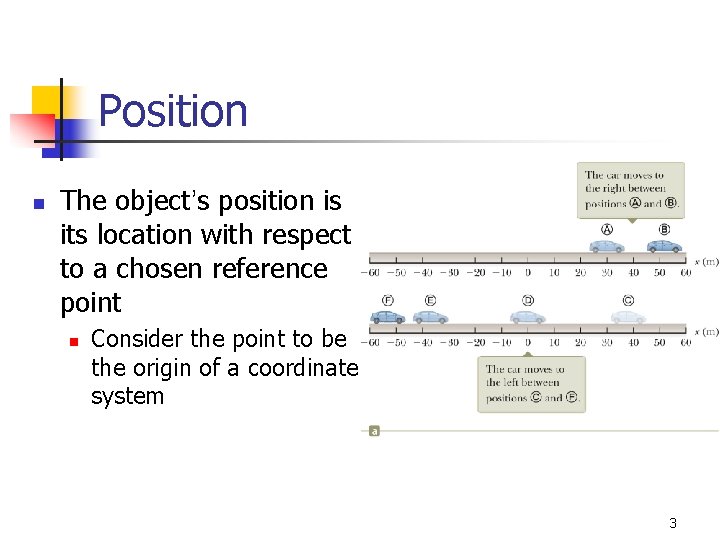
Position n The object’s position is its location with respect to a chosen reference point n Consider the point to be the origin of a coordinate system 3

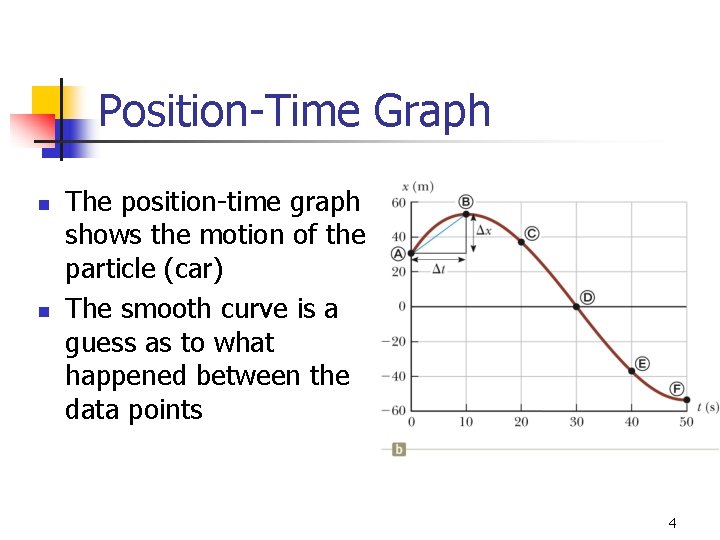
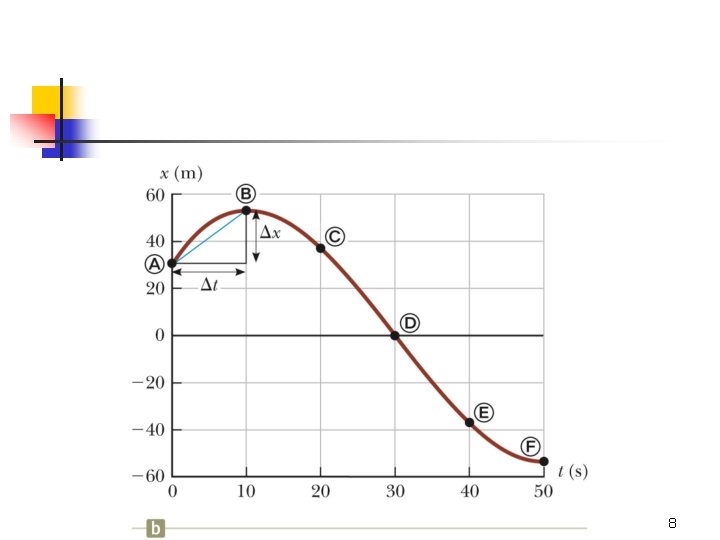
Position-Time Graph n n The position-time graph shows the motion of the particle (car) The smooth curve is a guess as to what happened between the data points 4

Displacement n Defined as the change in position during some time interval n n Represented as x x = xf – xi , where xi is the initial position and xf is the final position SI units are meters (m) x can be positive or negative Different than distance n Distance is the length of a path followed by a particle 5

Vectors and Scalars n Vector quantities need both magnitude (size or numerical value) and direction to completely describe them n n use + and – signs to indicate vector directions Scalar quantities are completely described by magnitude only 6

Average Velocity n n The average velocity is rate at which the displacement occurs The dimensions are length / time [L/T] The SI units are m/s Average velocity is also the slope of the line in the position – time graph 7

8

Average Speed n Speed is a scalar quantity same units as velocity n total distance / total time (average velocity=the particle’s displacement / its required time) n n The average speed is not (necessarily) the magnitude of the average velocity 9

Instantaneous Velocity n n n The general equation for instantaneous velocity is The instantaneous velocity indicates what is happening at every point of time The instantaneous velocity can be positive, negative, or zero 10

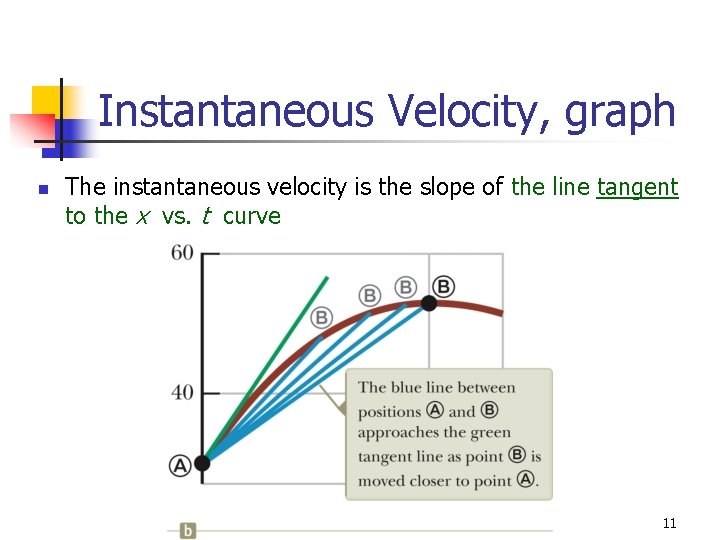
Instantaneous Velocity, graph n The instantaneous velocity is the slope of the line tangent to the x vs. t curve 11

A Note About Slopes n The slope of a graph of physical data n The ratio of change in the quantity represented on the vertical axis to the change in the quantity represented by the horizontal axis. n The slope has units n Unless both axes have the same units 12

Instantaneous Speed n n The instantaneous speed is the magnitude of the instantaneous velocity Remember that the average speed is not the magnitude of the average velocity 13

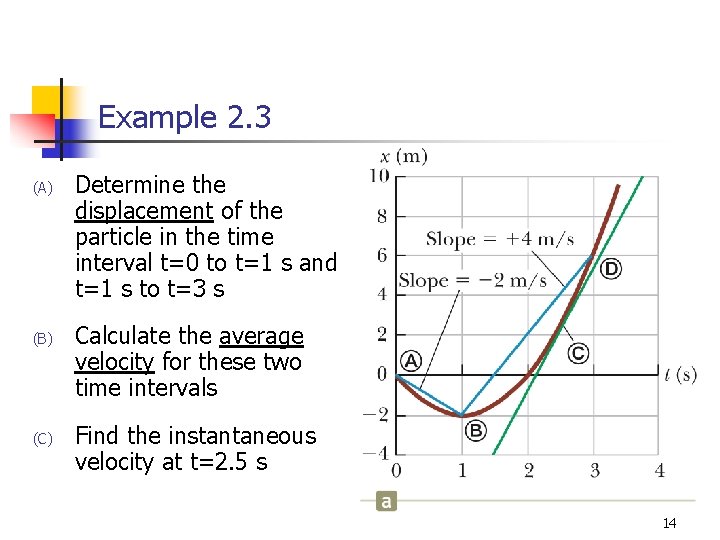
Example 2. 3 (A) (B) (C) Determine the displacement of the particle in the time interval t=0 to t=1 s and t=1 s to t=3 s Calculate the average velocity for these two time intervals Find the instantaneous velocity at t=2. 5 s 14

Particle Under Constant Velocity n Constant velocity indicates the instantaneous velocity at any instant during a time interval is the same as the average velocity during that time interval n vx = vx, avg n The mathematical representation n Common practice is to let ti = 0 and the equation becomes: xf = xi + vx t (for constant vx) 15

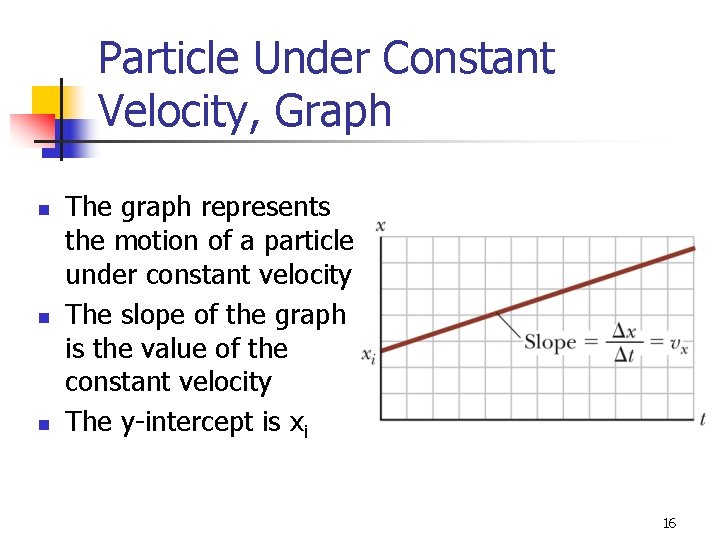
Particle Under Constant Velocity, Graph n n n The graph represents the motion of a particle under constant velocity The slope of the graph is the value of the constant velocity The y-intercept is xi 16

Average Acceleration n n Acceleration is the rate of change of the velocity Dimensions are L/T 2 SI units are m/s² In one dimension, positive and negative can be used to indicate direction 17

Instantaneous Acceleration n The instantaneous acceleration is the limit of the average acceleration as t approaches 0 18

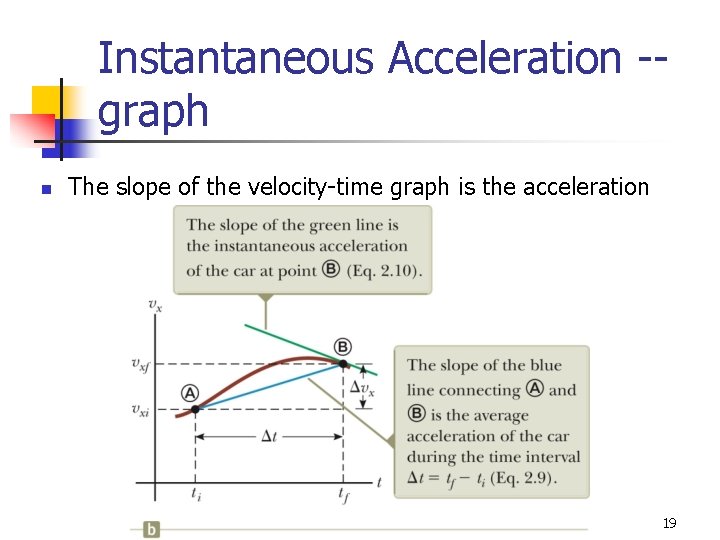
Instantaneous Acceleration -graph n The slope of the velocity-time graph is the acceleration 19

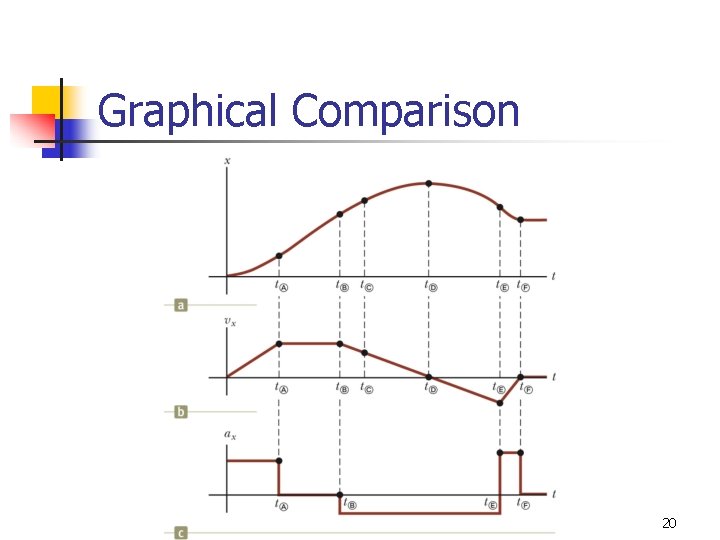
Graphical Comparison 20

Acceleration and Velocity, 1 n When an object’s velocity and acceleration are in the same direction, the object is speeding up n When an object’s velocity and acceleration are in the opposite direction, the object is slowing down 21

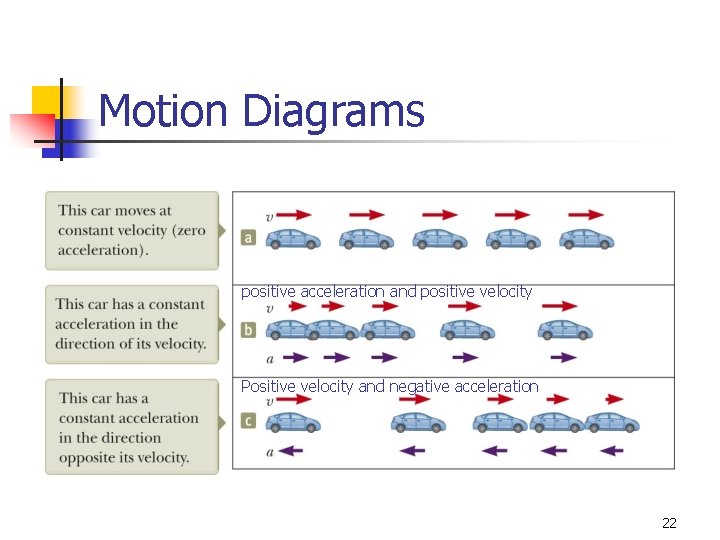
Motion Diagrams positive acceleration and positive velocity Positive velocity and negative acceleration 22

Kinematic Equations n n n The kinematic equations may be used to solve any problem involving one-dimensional motion with a constant acceleration You may need to use two of the equations to solve one problem Many times there is more than one way to solve a problem 23

Kinematic Equations, 1 n n n Can determine an object’s velocity at any time t when we know its initial velocity and its acceleration Does not give any information about displacement 24

Kinematic Equations, 2 n n For constant acceleration, The average velocity can be expressed as the arithmetic mean of the initial and final velocities 25

Kinematic Equations, 3 n n n For constant acceleration, This gives you the position of the particle in terms of time and velocities Doesn’t give you the acceleration 26

Kinematic Equations, 4 n n n For constant acceleration, Gives final position in terms of velocity and acceleration Doesn’t tell you about final velocity 27

Kinematic Equations, 5 n n n For constant a, Gives final velocity in terms of acceleration and displacement Does not give any information about the time 28

Kinematic Equations -summary 29

When a = 0 n When the acceleration is zero, n n n vxf = vxi = vx xf = x i + v x t The constant acceleration model reduces to the constant velocity model 30

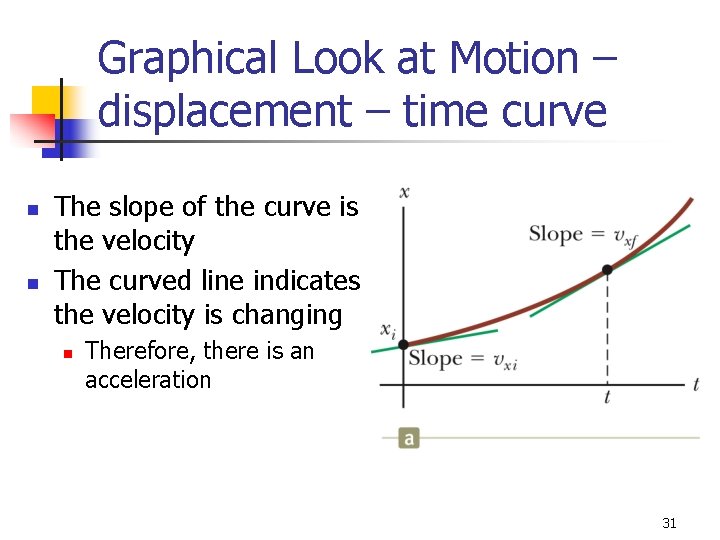
Graphical Look at Motion – displacement – time curve n n The slope of the curve is the velocity The curved line indicates the velocity is changing n Therefore, there is an acceleration 31

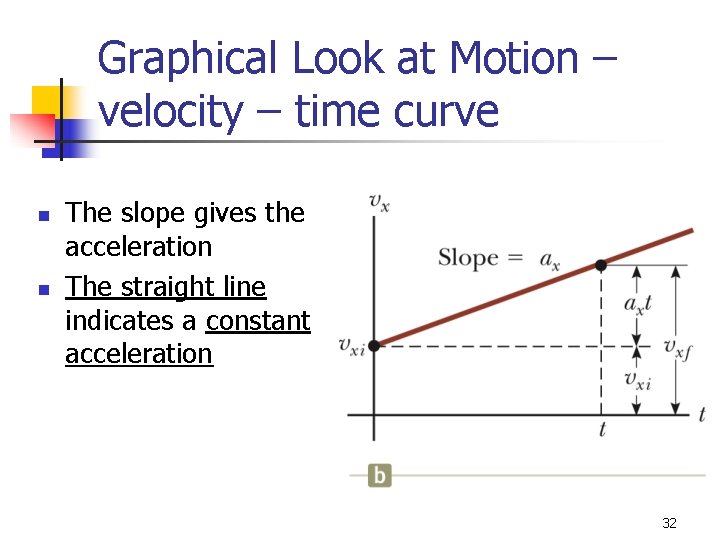
Graphical Look at Motion – velocity – time curve n n The slope gives the acceleration The straight line indicates a constant acceleration 32

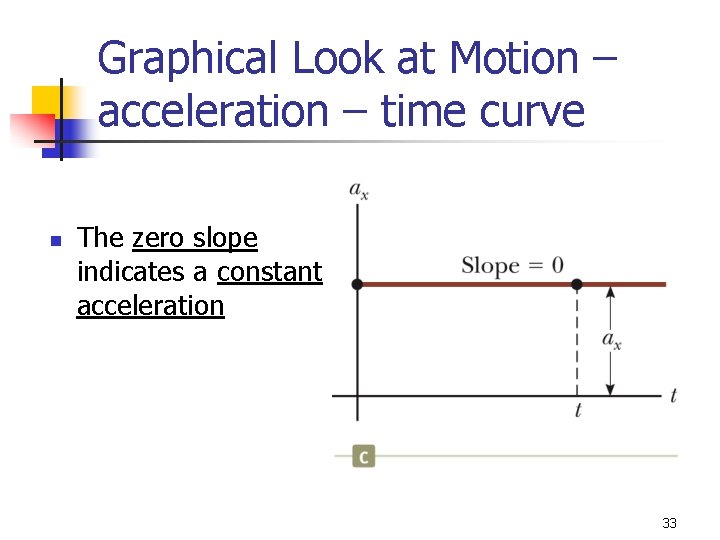
Graphical Look at Motion – acceleration – time curve n The zero slope indicates a constant acceleration 33

Freely Falling Objects n A freely falling object is any object moving freely under the influence of gravity alone regardless of its initial motion of the object n n n Dropped – released from rest Thrown downward Thrown upward 34

Acceleration of Freely Falling Object n The acceleration of an object in free fall is directed downward, regardless of the initial motion n The magnitude of free fall acceleration is g = 9. 80 m/s 2 n g decreases with increasing altitude g varies with latitude n 9. 80 m/s 2 is the average at the Earth’s surface n 35

Acceleration of Free Fall, cont. n We will neglect air resistance Free fall motion is constantly accelerated motion in one dimension n Let upward be positive n n Use the kinematic equations with ay = -g = -9. 80 m/s 2 36

Free Fall Example n n Initial velocity at A is upward (+) and acceleration is -g (-9. 8 m/s 2) At B, the velocity is 0 and the acceleration is -g (-9. 8 m/s 2) At C, the velocity has the same magnitude as at A, but is in the opposite direction The displacement is – 50. 0 m (it ends up 50. 0 m below its starting point) 37

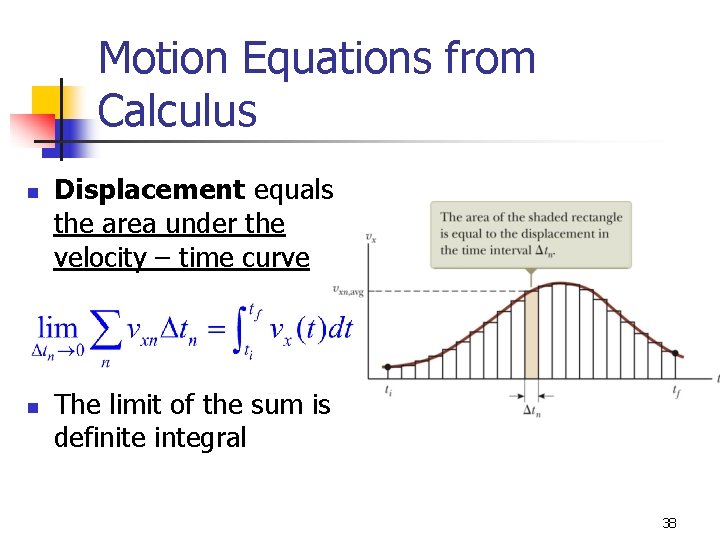
Motion Equations from Calculus n n Displacement equals the area under the velocity – time curve The limit of the sum is a definite integral 38

Kinematic Equations – General Calculus Form 39

Kinematic Equations – Calculus Form with Constant Acceleration n The integration form of vf – vi gives n The integration form of xf – xi gives 40

General Problem Solving Strategy n n Conceptualize Categorize Analyze Finalize 41

Problem Solving – Conceptualize n n n Think about and understand the situation Make a quick drawing of the situation Gather the numerical information n n Focus on the expected result n n Include algebraic meanings of phrases Think about units Think about what a reasonable answer should be 42

Problem Solving – Categorize n Simplify the problem n n Can you ignore air resistance? Model objects as particles Classify the type of problem Try to identify similar problems you have already solved 43

Problem Solving – Analyze n n Select the relevant equation(s) to apply Solve for the unknown variable Substitute appropriate numbers Calculate the results n n Include units Round the result to the appropriate number of significant figures 44

Problem Solving – Finalize n Check your result n n Does it have the correct units? Does it agree with your conceptualized ideas? Look at limiting situations to be sure the results are reasonable Compare the result with those of similar problems 45

Problem Solving – Some Final Ideas n n When solving complex problems, you may need to identify sub-problems and apply the problem-solving strategy to each subpart These steps can be a guide for solving problems in this course 46