Chapter 2 Measurement Ch 2 1 Measurement A

Chapter 2 Measurement

Ch 2. 1 - Measurement A. Measurement is a way to describe the world with numbers 1. Answers questions such as how much, how long, how far, etc. 2. Can answer questions of volume, mass weight, temperature and speed

a) Volume – the amount of space an object occupies b) Mass – how much matter is in an object c) Weight – magnitude of gravitational force acting on an object d) Speed – relationship between a distance traveled and time taken to travel

B. Estimation 1. Is a means of making a rough measurement of an object

C. Precision & Accuracy 1. Precision – a description of how close measurements are to each other ex: If you measure the same object 5 times and get the exact same result you have been precise

2. Precision (continued) - also how small of a unit an object was measured to ex: a ruler that shows mm is more precise than one that only shows cm

3. Accuracy – how close your measured value is to the accepted value (correctness) ex: A clock with a second hand is very precise, however if it is set an hour off, the time would not be accurate ex: If you measure the length of a table to be 1. 95 m you have been more precise than if you just said 2 m; however if the table is 3 m you were not very accurate

Precision vs. Accuracy High Precision / Low Accuracy High Accuracy / Low Precision

4. Significant Digits - the # of digits that reflect the precision of a measurement a) Digits other than 0 are always significant b) Final 0’s after a decimal are significant ex: 6. 545600 (shows this was measured to the millionths place)

c) 0’s between any other digits are significant ex: 507. 0301 (present as place holders) d) 0’s in a whole # may or may not be sig. ex: 1650 (depends on if it was a rounded # or not) e) A # obtained by counting instead of measuring is significant ex: number of people in a room

D. Rules for Significant Figures 1. For x and ÷ you must determine the amount of sig. digits in each # of the problem. The # of sig. digits in the answer will be the lesser number from the problem. ex: 6. 23 x 3. 1 = 19. 313 3 2 2

2. For + and – you must determine the place value of each # in the problem. The sig. digits of the answer is determined by the # that is least precise. ex: 6. 23 + 3. 1 9. 33 Hundredths place Tenths place

Ch 2. 2 – SI Units A. SI - Stands for the International System of Units aka the Metric System 1. Developed by French scientists in 1793 commissioned under Louis XVI 2. Today has become the most widely used system of measurement in the world for both commerce and science

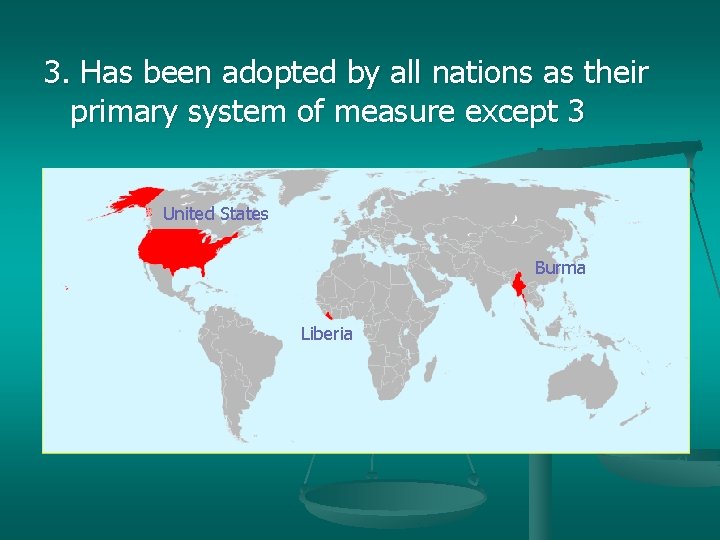
3. Has been adopted by all nations as their primary system of measure except 3 United States Burma Liberia

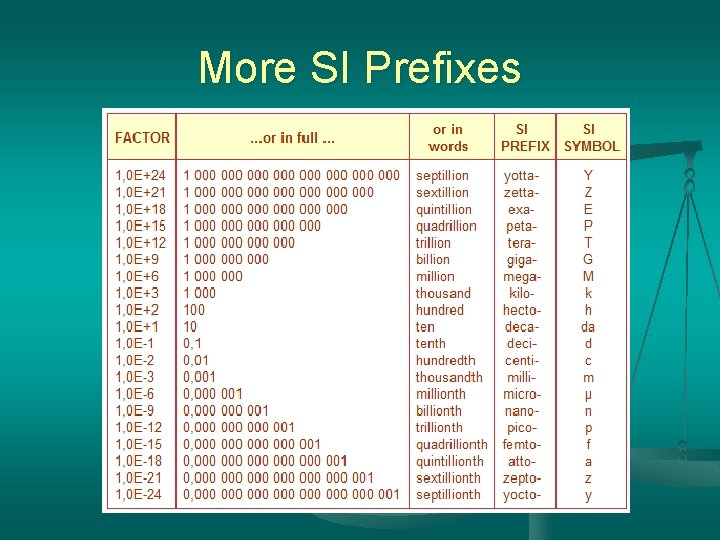
4. Units are based on the number 10 5. Uses base units which may have an attached prefix to change the base into a larger or smaller unit ilo K He o ct a c e D E i c S De BA i C t n e lli i M K H D * d c m 1000 10 1 0. 01 0. 001

More SI Prefixes

B. SI Units 1. Length – meter (m) 2. Volume – liter (l or m 3) 3. Mass – gram (g) o 4. Temperature – Kelvin (K) or Celsius ( C)

5. Time – second (s) 6. Rate/Speed – meters/second (m/s) 7. Weight – Newton (N) 8. Electric Current – Ampere (A) 9. Pressure – Pascal (Pa)

C. SI Units vs. US Customary System 1. 1 m = 3. 28 ft (about 3’ 3”) 2. 1 km = 0. 62 miles (1 mi = 1. 6 km) 3. 1 0 C = 33. 8 0 F (1 0 F = -17. 2 0 C) 4. 1 K = -457. 6 0 F (1 0 F = 255. 7 K)

Ch 2. 3 – Drawings, Tables & Graphs A. Are used to represent data in an organized manner 1. Tables – display information in rows and columns so that it is easier to read and understand

Which is Easier to Interpret? n In container A, the water temperature was recorded to be 40 C and there was 56 guppy movements. In Container B, the water was at 42 C and the number of guppy movements increased to 70. In container C, the water temperature was reduced to 36 C and the number of times the guppy moved also dropped bringing the count to 46. . OR

2. Graph – used to collect, organize and summarize data in a visual way a) Generally the relationships between data are seen more clearly in a graph form b) There are 3 basic types of graphs: line, bar, circle

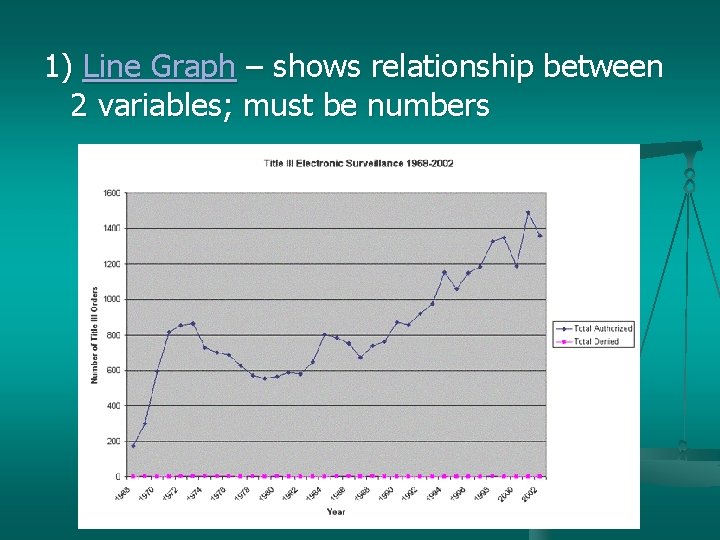
1) Line Graph – shows relationship between 2 variables; must be numbers

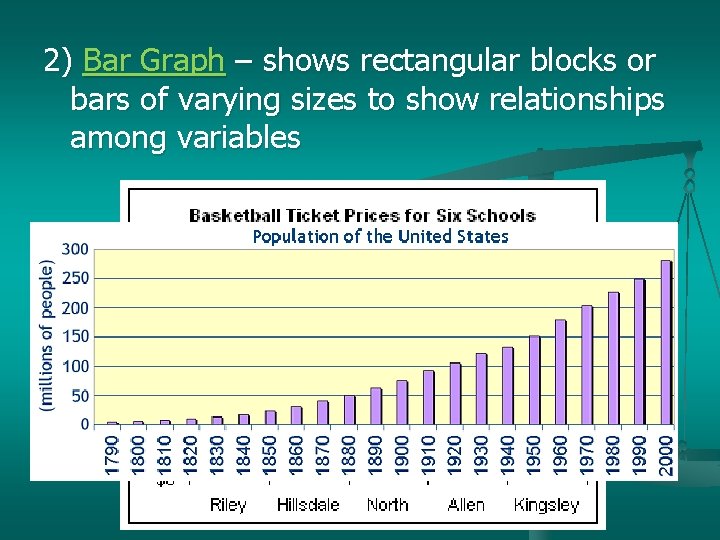
2) Bar Graph – shows rectangular blocks or bars of varying sizes to show relationships among variables

3) Circle Graph - (aka Pie Graph) shows the parts of a whole; each section represents a fraction of the total - A circle graph has 3600 You must determine what part of that 360 each section will be equal to (**See example p. 58)