Chapter 2 Matrix Algebra 2 1 Matrix operations

Chapter 2 Matrix Algebra • 2. 1 Matrix operations 矩阵运算 • 2. 2 The inverse of matrix 矩阵的逆 • 2. 3 Characterizations of invertible matrices 1

A=[a 1 a 2 … an] = =( aij )m n = [ aij ] m n aj―the jth column vector of A aij―the scalar entry in the ith row and jth column of A. 2

• a 11, a 22, a 33, …――diagonal entries, main diagonal of A • A diagonal matrix is a square matrix whose nondiagonal entries are zero 3

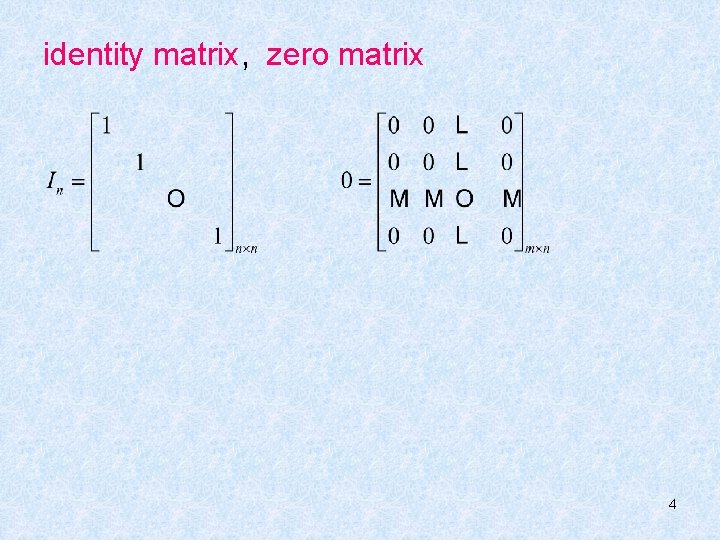
identity matrix, zero matrix 4

Sums and Scalar Multiples • • • Equal sum A+B scalar multiple r. A, -A = (-1)A A-B=A+(-B) 相等 相加，和 数乘，数量积 负矩阵 相减，差 5

• THEOREM 1 Let A, B, C be matrices of the same size, and let r and s be scalars. a. A+B=B+A d. r(A+B) = r. A + r. B b. A+(B+C) = (A+B)+C e. (r + s) A = r. A + s. A c. A+O = A f. r ( s A ) = (r s)A 6

Matrix Multiplication 矩阵乘法 • DEFINITION AB = A [b 1 b 2 … bp] = [Ab 1 Ab 2 … Abp] 7

Row-Column Rule For Computing AB cij=(AB)ij = ai 1 b 1 j + ai 2 b 2 j + … + ainbnj 8

Properties of Matrix Multiplication • THEOREM 2 a. Am n(Bn l. Cl k) = (AB)C b. A ( B + C ) = AB + AC c. ( B + C ) A = BA + CA d. r(AB) = (r. A)B = A (r. B) e. Im. A = AIn If AB = BA, then we say that A and B commute with one another. 9

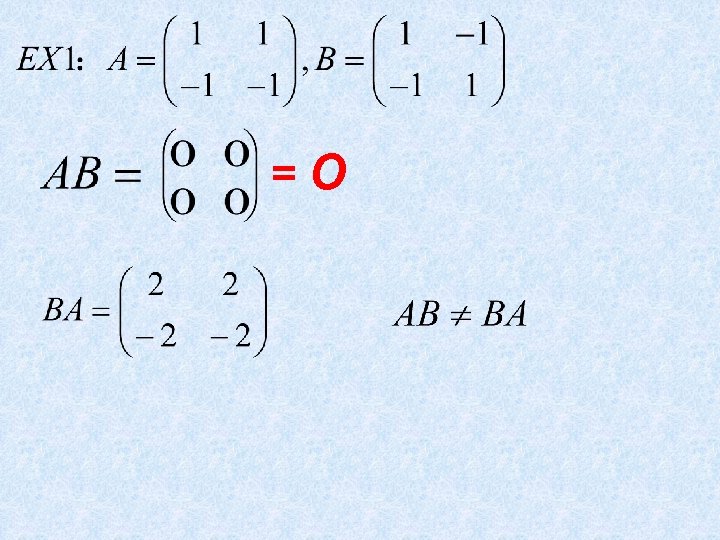
=O

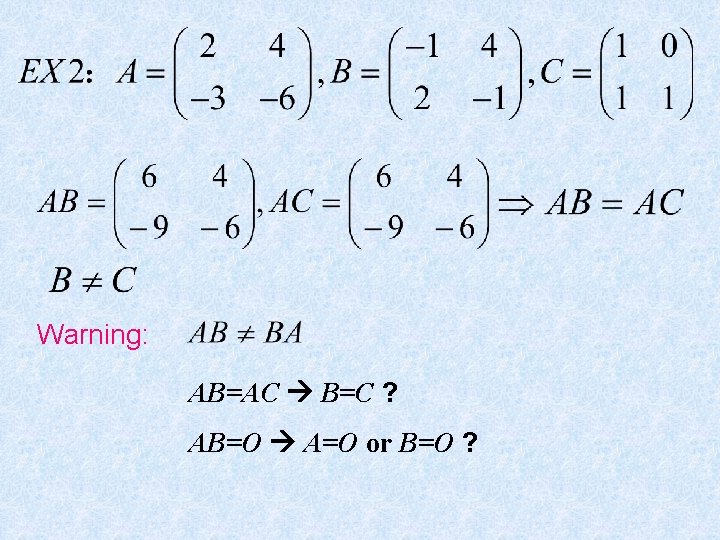
Warning: AB=AC B=C ? AB=O A=O or B=O ?

Powers of a Matrix 幂 • An n , Ak = A·A·…·A I n = I, 0 n = 0 12

The Transpose of a Matrix 矩阵的转置 • Given an m×n matrix A, the transpose of A is the n×m matrix, denoted by AT, whose columns are formed from the corresponding rows of A. 13

• THEOREM 3 a. (AT )T = A b. (A+B)T = AT + BT c. (r. A)T = r. AT d. (AB)T = BTAT 14

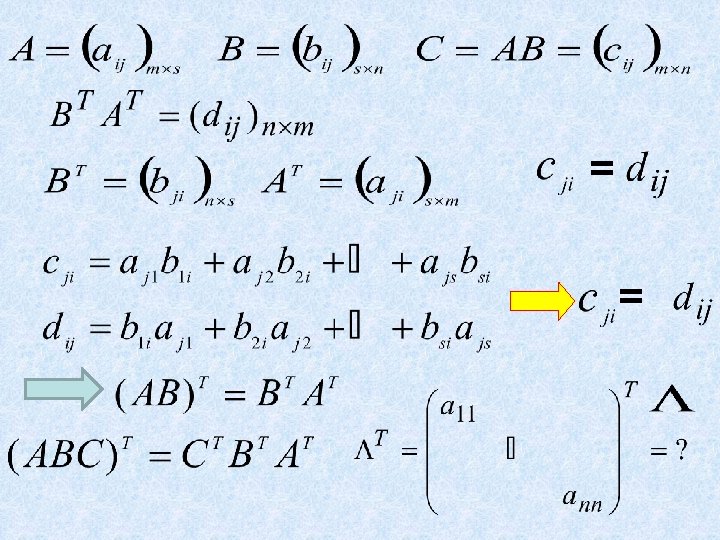
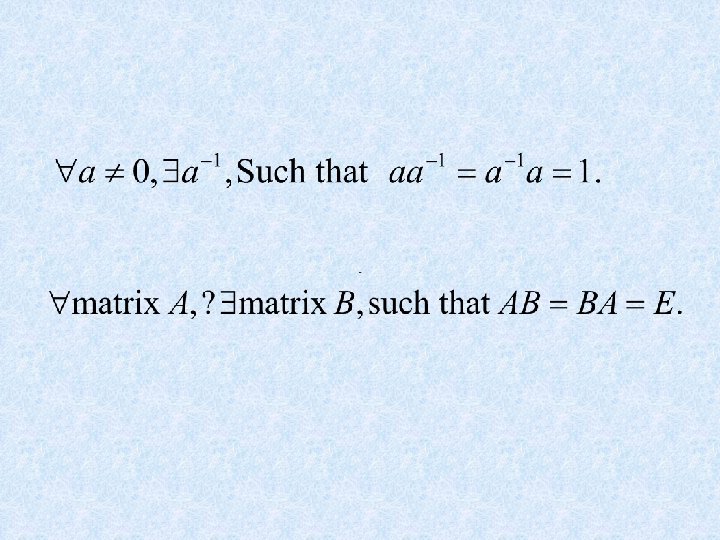
2. 2 The Inverse of a Matrix 矩阵的逆 • DEFINITION An n×n matrix A is said to be invertible if there is an n×n matrix C such that CA=In and AC=In. In this case, C is an inverse of A. A matrix that is not invertible is called a singular matrix, and an invertible matrix is called a nonsingular matrix. 奇异矩阵，非奇异矩阵 If C = A-1, C is uniquely determined by A. WHY? If B= A-1 , then B=IB=(CA)B=C(AB)=CI=C. 17

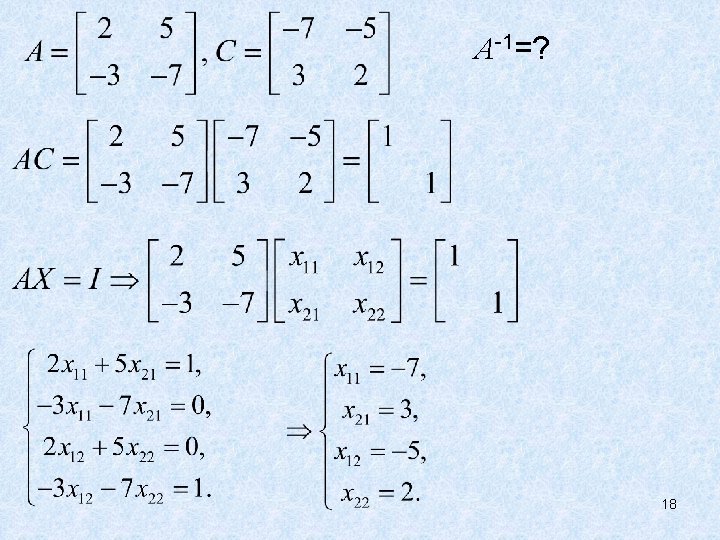
A-1=? 18

• THEOREM 4 Let , if ad – bc 0, then A is invertible and. If ad – bc = 0, then A is not invertible 19

Proof: If ad – bc = 0, then A is not invertible Let , then or Ax=0 has many solutions. 20

• The quantity ad – bc is called the determinant of A, and we write det A = ad – bc. 行列式 21

• THEOREM 5 If A is an invertible n×n matrix, then for each b in Rn, the equation Ax = b has the unique solution x =A-1 b. 22

• THEOREM 6 a. If A is an invertible matrix, then A-1 is invertible, and (A-1)-1 = A b. If A an B are invertible n×n matrices , then so is AB , and (AB)-1 = B-1 A -1 c. If A is an invertible matrix, then so is AT, and ( AT )-1 = ( A-1 )T. 23

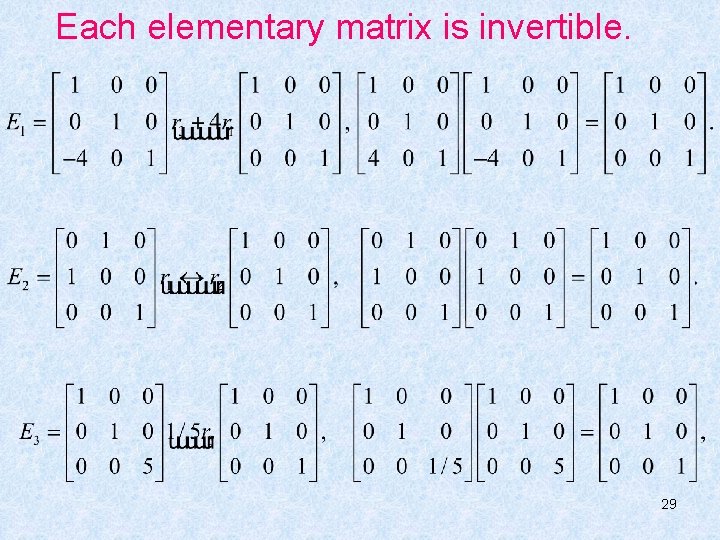
• Elementary Matrices An elementary matrix is one that is obtained by performing a single elementary row operation on an identity matrix. Each elementary matrix is invertible. 24

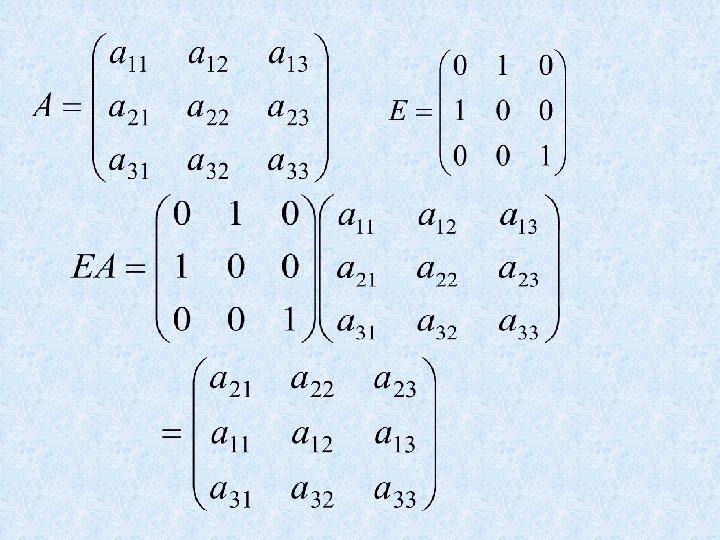
• If an elementary row operation is performed on an m×n matrix A, the resulting matrix can be written as EA, where the m×m matrix E is created by performing the same row operation on Im. 26

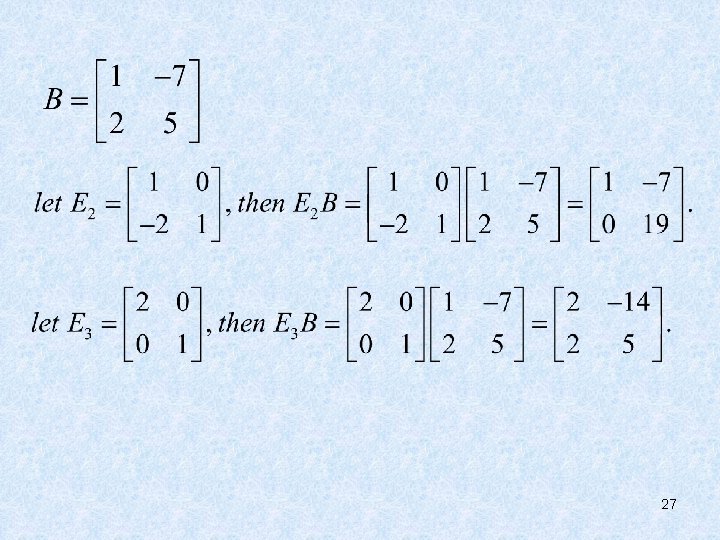
27

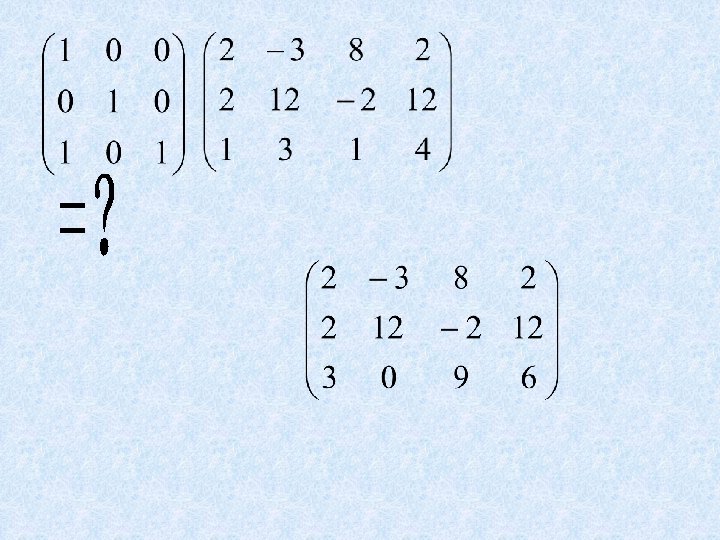
Each elementary matrix is invertible. 29

Each elementary matrix is invertible. 30

• THEOREM 7 An n×n matrix A is invertible if and only if A is row equivalent to In, and in this case, any sequence of elementary row operations that reduce A to In also transforms In into A-1. 31

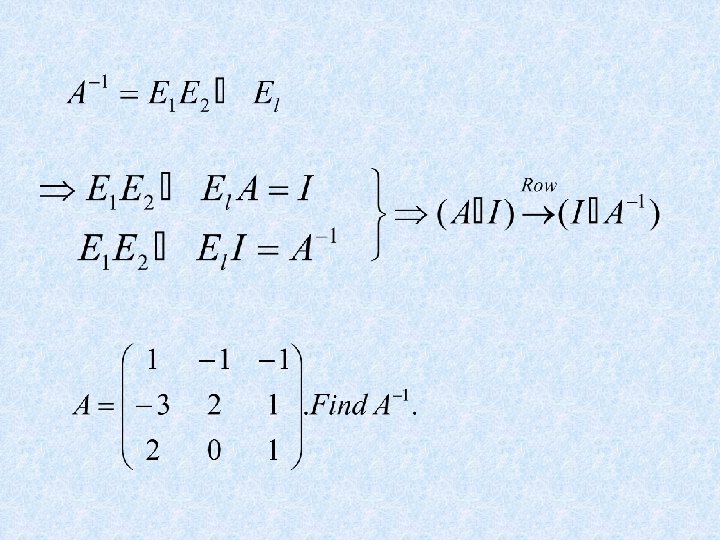
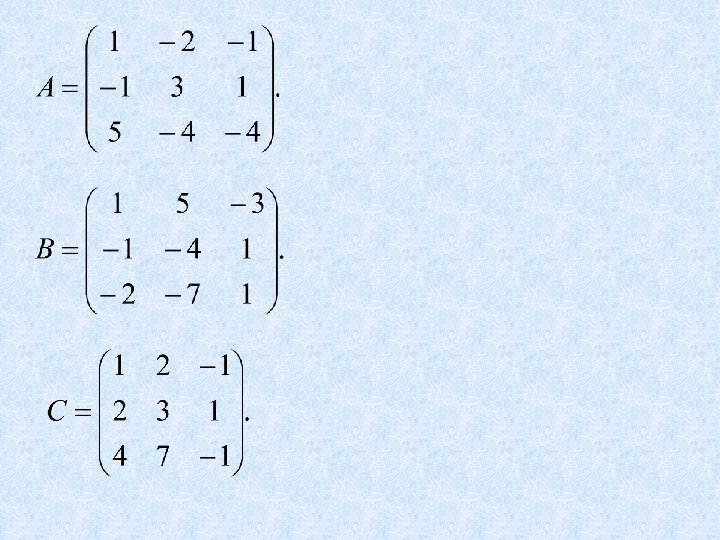
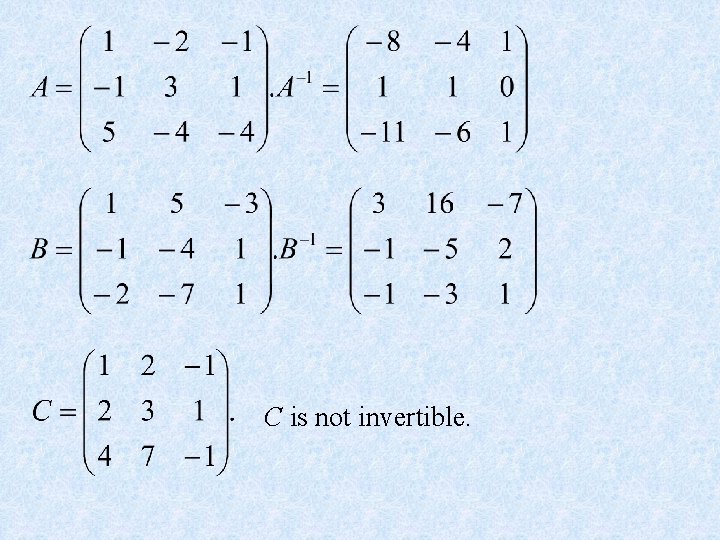
C is not invertible.

36

37

• An Algorithm for Finding A-1 Row reduce the augmented matrix [ A I ]. If A is row equivalent to I, then [ A I ] is equivalent to [ I A-1 ]. Otherwise, A does not have an inverse. 38

Another View of Matrix Inversion First and third columns of