Chapter 2 Matrices Definition of a matrix 1














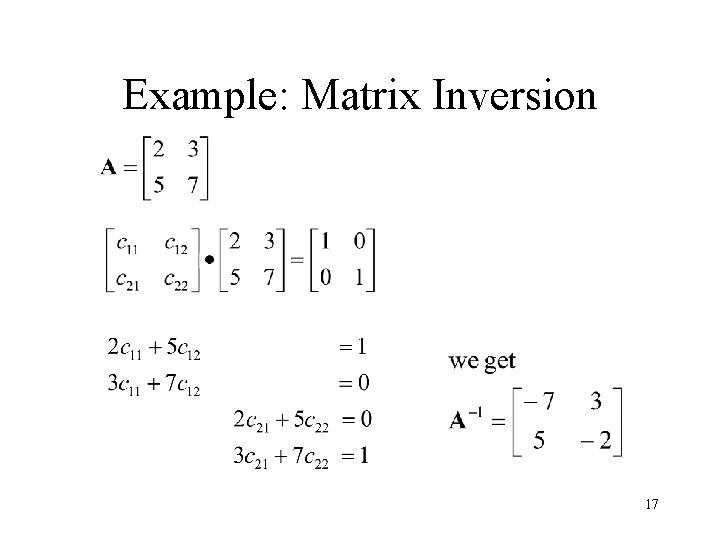

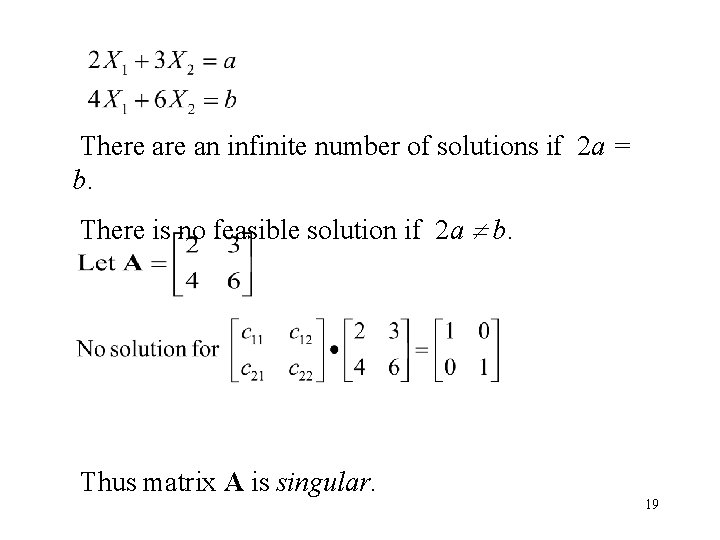








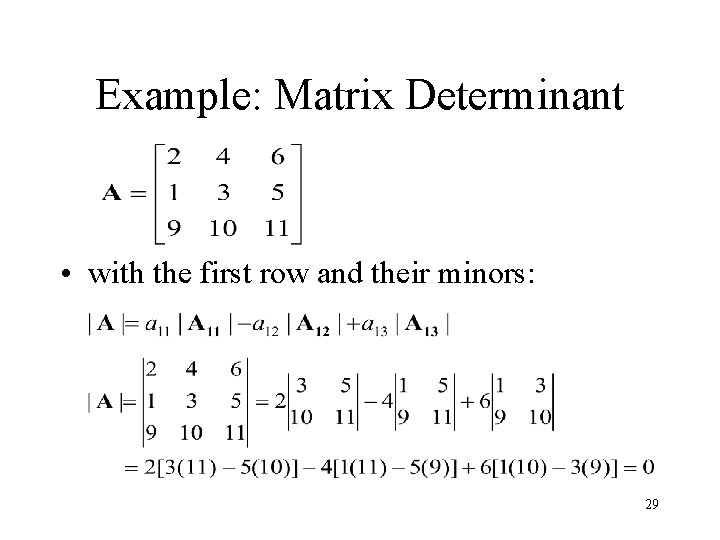









- Slides: 38

Chapter 2 Matrices • Definition of a matrix 1

A system of 3 equations: Represented by a matrix: 2

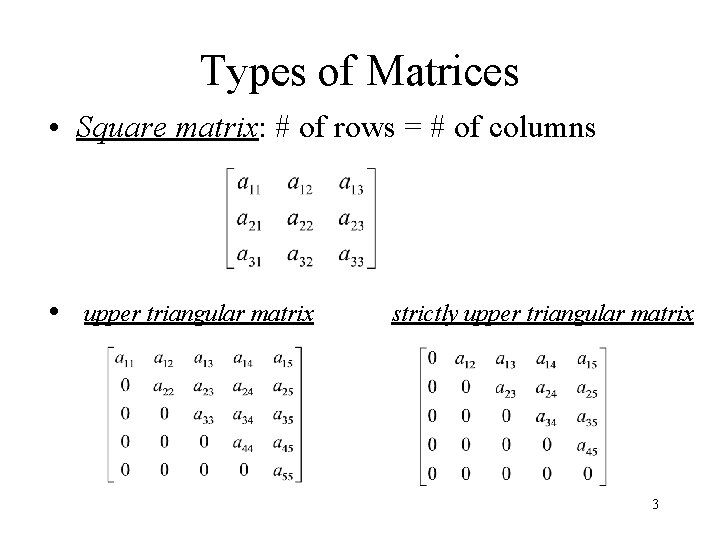
Types of Matrices • Square matrix: # of rows = # of columns • upper triangular matrix strictly upper triangular matrix 3

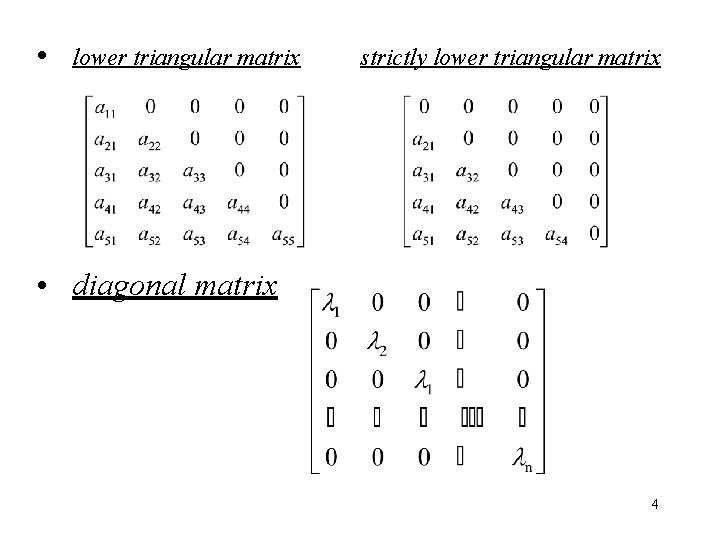
• lower triangular matrix strictly lower triangular matrix • diagonal matrix 4

• banded matrix a square matrix with elements of zero except for the principal diagonal and values in the positions adjacent to the diagonal. • tridiagonal matrix 5

• unit matrix: 1 on the principal diagonal • null matrix: All elements are zero. 6

• symmetric matrix: a square matrix in which • skew-symmetric matrix: a square matrix in which and j for all i 7

• transpose of matrix A: AT • (AT) T = A 8

Matrix Operations • Matrix equality • Matrix addition and subtraction C = A + B = B + A (commutative) C=A-B 9

• Example: Matrix addition and subtraction 10

Matrix Multiplication • One example 11

Rules of Matrix Multiplication 1. # of columns in A = # of rows in B 2. # of rows in C = # of rows in A 3. # of columns in C = # of columns in B 4. 12

5. Matrix multiplication is not commutative 6. Matrix multiplication is associative 13

Example: Matrix Multiplication 14

Matrix Multiplication by a Scalar An example: 15

Matrix Inversion where A-1 is the inverse of A, and I is the unit matrix 16
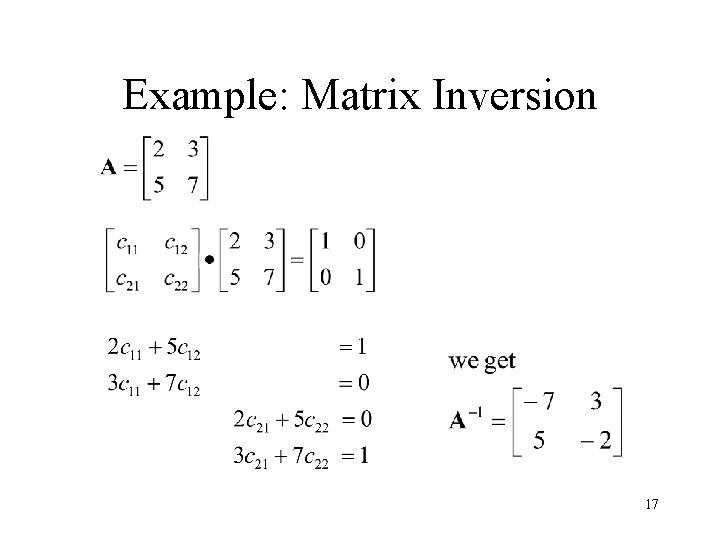
Example: Matrix Inversion 17

Matrix Singularity • If the inverse of a matrix A exists, then A is said to be nonsingular. • If the inverse of a matrix A does not exist, then A is said to be singular. • If matrix A is singular, then the linear system of simultaneous equations represented by A has no unique solution. 18
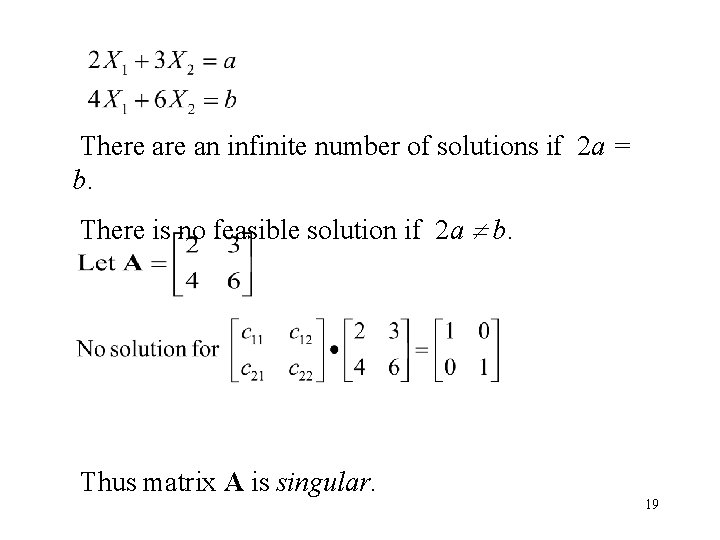
There an infinite number of solutions if 2 a = b. There is no feasible solution if 2 a b. Thus matrix A is singular. 19

• trace of a square matrix = sum of diagonal elements • matrix augmentation: addition of a column or columns to the initial matrix 20

• matrix partition 21

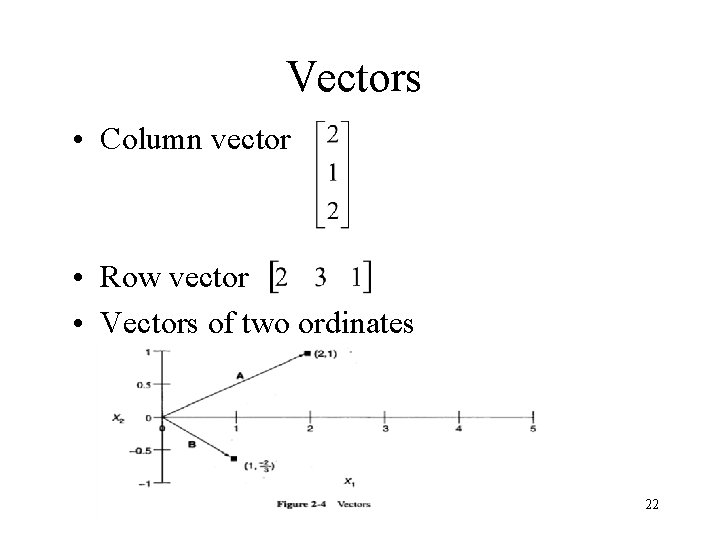
Vectors • Column vector • Row vector • Vectors of two ordinates 22

• orthogonal vectors Two vectors are said to be orthogonal if their product is equal to zero. If two vector are orthogonal, they are perpendicular to each other in the n-dimensional space. 23

• normalized vectors A vector is normalized by dividing each element by its length. A normalized vector has a length 1. Two vectors that are both normalized and orthogonal to each other are said to be orthonormal vectors. 24

Example: Vectors 25

Normalized vectors: 26

Determinants • A determinant of a matrix A is denoted by |A|. • The determinant of a 2 2 matrix: • The determinant of a 3 3 matrix: 27

• The minor of aij, denoted by Aij, is the matrix after removing row i and column j. • The determinant of an n n matrix: • The general expression for the determinant of an n n matrix: 28
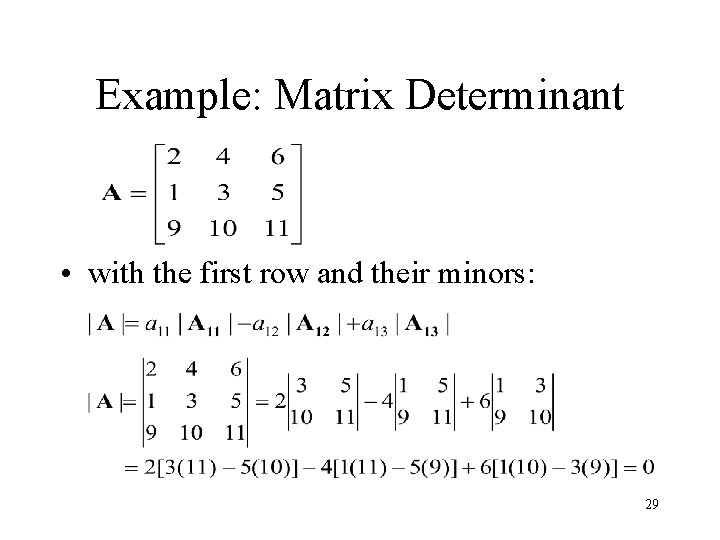
Example: Matrix Determinant • with the first row and their minors: 29

• with the second column and their minors: • Since |A|=0, A is a singular matrix; that is the inverse of A doest not exist. 30

Properties of Determinants 1. If the values in any row (column) are proportional to the corresponding values in another row(column), the determinant equals zero 31

2. If all the elements in any row(column) equal zero, the determinant equals zero. 3. If all the elements of any row(column) are multiplied by a constant c, the value of the determinant is multiplied by c. 32

4. The value of the determinant is not changed by adding any row (column) multiplied by a constant c to another row (column). 5. If any two rows (columns) are interchanged, the sign of the determinant is changed. 33

6. The determinant of a matrix equals that of its transpose; that is, |A| = |AT|. 7. If a matrix A is placed in diagonal form, then the product of the elements on the diagonal equals the determinant of A. 34

8. If a matrix A has a zero determinant, then A is a singular matrix; that is, the inverse of A does not exist. 35

Rank of A Matrix • A matrix of r rows and c columns is said to be of order r by c. If it is a square matrix, r by r, then the matrix is of order r. • The rank of a matrix equals the order of highestorder nonsingular submatrix. 36

Example 1: Rank of Matrix 3 square submatrices: Each of these has a determinant of 0, so the rank is less than 2. Thus the rank of R is 1. 37

Example 2: Rank of Matrix Since |A|=0, the rank is not 3. The following submatrix has a nonzero determinant: Thus, the rank of A is 2. 38