Chapter 2 Mathematical Tools of Quantum Mechanics Hilbert

Chapter 2 Mathematical Tools of Quantum Mechanics

Hilbert space • Let’s recall for Cartesian 3 D space: • A vector is a set of 3 numbers, called components – it can be expanded in terms of three unit vectors (basis) • The basis spans the vector space • Inner (dot, scalar) product of 2 vectors is defined as: • Length (norm) of a vector

Hilbert space

Hilbert space • Hilbert space: • Its elements are functions (vectors of Hilbert space) • The space is linear: if φ and ψ belong to the space then φ + ψ, as well as aφ (a – constant) also belong to the space David Hilbert (1862 – 1943)

Hilbert space • Hilbert space: • Inner (dot, scalar) product of 2 vectors is defined as: • Length (norm) of a vector is related to the inner product as: David Hilbert (1862 – 1943)

Hilbert space • Hilbert space: • The space is complete, i. e. it contains all its limit points (we will see later) • Example of a Hilbert space: L 2, set of squareintegrable functions defined on the whole interval David Hilbert (1862 – 1943)

Wave function space • Recall: • Thus we should retain only such functions ψ that are well-defined everywhere, continuous, and infinitely differentiable • Let us call such set of functions F • F is a subspace of L 2 • For two complex numbers λ 1 and λ 2 it can be shown that if 2. A

Scalar product • In F the scalar product is defined as: • Properties of the scalar product: • φ and ψ are orthogonal if • Norm is defined as 2. A. 1

Scalar product 2. A. 1 • Schwarz inequality Karl Hermann Amandus Schwarz (1843 – 1921)

Linear operators • Linear operator A is defined as: • Examples of linear operators: • Parity operator: • (Multiplication by) coordinate operator: • Differentiation operator: 2. A. 1

Linear operators • Product of operators: • In general: • Commutator: • Example: 2. A. 1

Orthonormal bases • A countable set of functions • is called orthonormal if: • It constitutes a basis if every function in F can be expanded in one and only one way: • Recall for 3 D vectors: 2. A. 2

Orthonormal bases • For two functions • a scalar product is: • Recall for 3 D vectors: 2. A. 2

Orthonormal bases • This means that • Closure relation 2. A. 2

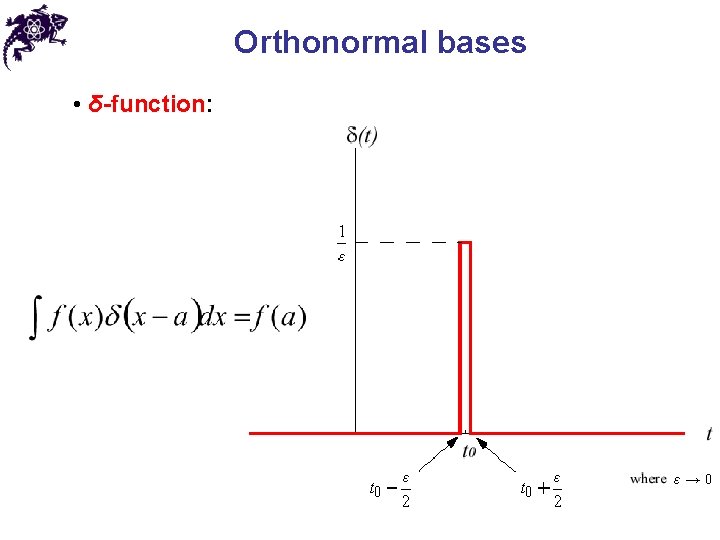
Orthonormal bases • δ-function:

Orthonormal bases 2. A. 3 • A set of functions labelled by a continuous index α • is called orthonormal if: • It constitutes a basis if every function in F can be expanded in one and only one way:

Orthonormal bases • For two functions • a scalar product is: 2. A. 3

Orthonormal bases • This means that • Closure relation 2. A. 3

Orthonormal bases • Useful relationship: 2. A. 3

Examples of orthonormal bases • Let us apply Fourier transform to function ψ(x): • Using functions of plane waves • we can write: 2. A. 3

Examples of orthonormal bases • For two functions • a scalar product is: 2. A. 3

Examples of orthonormal bases • This means that • Closure relation 2. A. 3

Examples of orthonormal bases • Let us consider a set of functions: • The set is orthonormal: • Functions in F can be expanded: 2. A. 3

Examples of orthonormal bases • For two functions • a scalar product is: 2. A. 3

Examples of orthonormal bases • This means that • Closure relation 2. A. 3

State vectors and state space • The same function ψ can be represented by a multiplicity of different sets of components, corresponding to the choice of a basis • These sets characterize the state of the system as well as the wave function itself • Moreover, the ψ function appears on the same footing as other sets of components 2. B. 1

State vectors and state space 2. B. 1 • Each state of the system is thus characterized by a state vector, belonging to state space of the system Er • As F is a subspace of L 2, Er is a subspace of the Hilbert space

Dirac notation 2. B. 2 • Bracket = “bra” x “ket” • < > = < | > = “< |” x “| >” Paul Adrien Maurice Dirac (1902 – 1984)

2. B. 2 Dirac notation • We will be working in the Er space • Any vector element of this space we will call a ket vector • Notation: • We associate kets with wave functions: • F and Er are isomporphic • r is an index labelling components Paul Adrien Maurice Dirac (1902 – 1984)

2. B. 2 Dirac notation • With each pair ok kets we associate their scalar product – a complex number • We define a linear functional (not the same as a linear operator!) on kets as a linear operation associating a complex number with a ket: • Such functionals form a vector space • We will call it a dual space Er* Paul Adrien Maurice Dirac (1902 – 1984)

2. B. 2 Dirac notation • Any element of the dual space we will call a bra vector • Ket | φ > enables us to define a linear functional that associates (linearly) with each ket | ψ > a complex number equal to the scalar product: • For every ket in Er there is a bra in Er* Paul Adrien Maurice Dirac (1902 – 1984)

Dirac notation 2. B. 2 • Some properties: Paul Adrien Maurice Dirac (1902 – 1984)

Linear operators • Linear operator A is defined as: • Product of operators: • In general: • Commutator: • Matrix element of operator A: 2. B. 3

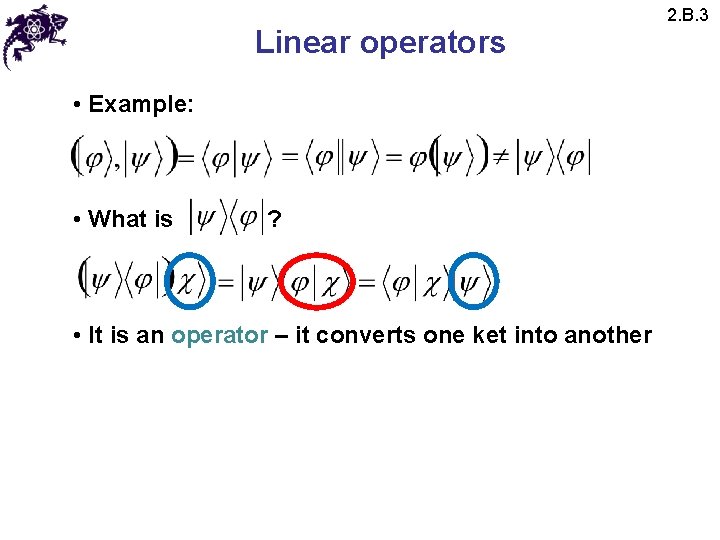
Linear operators • Example: • What is ? • It is an operator – it converts one ket into another 2. B. 3

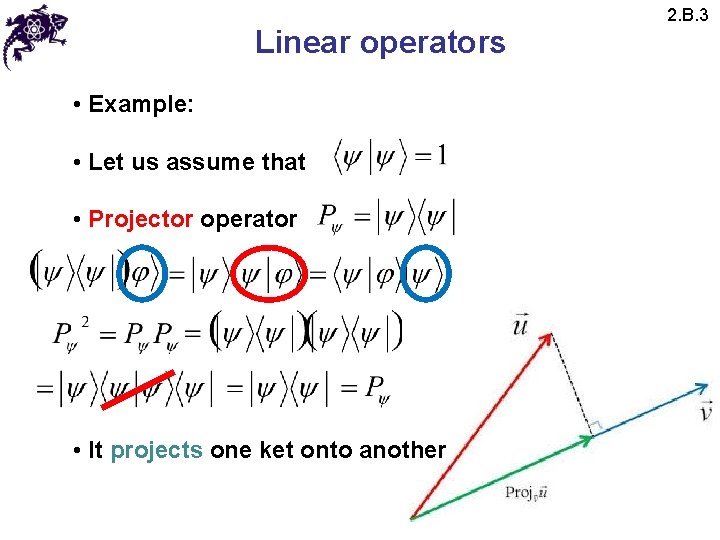
Linear operators • Example: • Let us assume that • Projector operator • It projects one ket onto another 2. B. 3

Linear operators • Example: • Let us assume that • These kets span space Eq, a subspace of E • Subspace projector operator • It projects a ket onto a subspace of kets 2. B. 3

Linear operators • Recall matrix element of a linear operator A: • Since a scalar product depends linearly on the ket, the matrix element depends linearly on the ket • Thus for a given bra and a given operator we can associate a number that will depend linearly on the ket • So there is a new linear functional on the kets in space E, i. e. , a bra in space of E*, which we will denote • Therefore 2. B. 4

Linear operators • Operator A associates with a given bra a new bra • Let’s show that this correspondence is linear 2. B. 4

2. B. 4 Linear operators • For each ket there is a bra associated with it • Hermitian conjugate (adjoint) operator: • This operator is linear (can be shown) Charles Hermite (1822 – 1901)

Linear operators 2. B. 4 • Some properties: Charles Hermite (1822 – 1901)

2. B. 4 Hermitian conjugation • To obtain Hermitian conjugation of an expression: • Replace constants with their complex conjugates • Replace operators with their Hermitian conjugates • Replace kets with bras • Replace bras with kets • Reverse order of factors Charles Hermite (1822 – 1901)

2. B. 4 Hermitian operators • For a Hermitian operator: • Hermitian operators play a fundamental role in quantum mechanics (we’ll see later) • E. g. , projector operator is Hermitian: • If: Charles Hermite (1822 – 1901)

Representations in state space • In a certain basis, vectors and operators are represented by numbers (components and matrix elements) • Thus vector calculus becomes matrix calculus • A choice of a specific representation is dictated by the simplicity of calculations • We will rewrite expressions obtained above for orthonormal bases using Dirac notation 2. C. 1

Orthonormal bases • A countable set of kets • is called orthonormal if: • It constitutes a basis if every vector in E can be expanded in one and only one way: 2. C. 2

Orthonormal bases • Closure relation • 1 – identity operator 2. C. 2

Orthonormal bases • For two kets • a scalar product is: 2. C. 3

Orthonormal bases • A set of kets labelled by a continuous index α • is called orthonormal if: • It constitutes a basis if every vector in E can be expanded in one and only one way: 2. C. 2

Orthonormal bases • Closure relation • 1 – identity operator 2. C. 2

Orthonormal bases • For two kets • a scalar product is: 2. C. 3

Representation of kets and bras 2. C. 3 • In a certain basis, a ket is represented by its components • These components could be arranged as a columnvector:

Representation of kets and bras • In a certain basis, a bra is also represented by its components • These components could be arranged as a rowvector: 2. C. 3

Representation of operators • In a certain basis, an operator is represented by matrix components: 2. C. 4

Representation of operators 2. C. 4

Representation of operators 2. C. 4

Representation of operators 2. C. 4

Representation of operators 2. C. 4

Representation of operators • For Hermitian operators: • Diagonal elements of Hermitian operators are always real 2. C. 4

Change of representations 2. C. 5

Change of representations 2. C. 5

Eigenvalue equations 2. D. 1 • A ket is called an eigenvector of a linear operator if: • This is called an eigenvalue equation for an operator • This equation has solutions only when λ takes certain values - eigenvalues • If: • then:

Eigenvalue equations 2. D. 1 • The eigenvalue is called nondegenerate (simple) if the corresponding eigenvector is unique to within a constant • The eigenvalue is called degenerate if there at least two linearly independent kets corresponding to this eigenvalue • The number of linearly independent eigenvectors corresponding to a certain eigenvalue is called a degree of degeneracy

Eigenvalue equations 2. D. 1 • If for a certain eigenvalue λ the degree of degeneracy is g: • then every eigenvector of the form • is an eigenvector of the operator A corresponding to the eigenvalue λ for any ci: • The set of linearly independent eigenvectors corresponding to a certain eigenvalue comprises a gdimensional vector space called an eigensubspace

Eigenvalue equations 2. D. 1 • Let us assume that the basis is finite-dimensional, with dimensionality N • This is a system of N linear homogenous equations for N coefficients cj • Condition for a non-trivial solution:

Eigenvalue equations 2. D. 1 • This equation is called the characteristic equation • This is an Nth order equation in and it has N roots – the eigenvalues of the operator • Condition for a non-trivial solution:

Eigenvalue equations 2. D. 1 • Let us select λ 0 as one of the eigenvalues • If λ 0 is a simple root of the characteristic equation, then we have a system of N – 1 independent equations for coefficients cj • From linear algebra: the solution of this system (for one of the coefficients fixed) is

Eigenvalue equations 2. D. 1 • Let us select λ 0 as one of the eigenvalues • If λ 0 is a multiple (degenrate) root of the characteristic equation, then we have less than N – 1 independent equations for coefficients cj • E. g. , if we have N – 1 independent equations then (from linear algebra) the solution of this system is

2. D. 2 Eigenproblems for Hermitian operators • For: • Therefore λ is a real number • Also: • If: • Then: • But:

Observables 2. D. 2 • Consider a Hermitian operator A whose eigenvalues form a discrete spectrum • The degree of degeneracy of a given eigenvalue an will be labelled as gn • In the eigensubspace En we consider gn linearly independent kets: • If • Then

Observables 2. D. 2 • Inside each eigensubspace • Therefore: • If all these eigenkets form a basis in the state space, then operator A is called an observable

Observables 2. D. 2 • For an eigensubspace projector • These relations could be generalized for the case of continuous bases • E. g. , a projector is an observable

Observables 2. D. 3 • If • Then • If a is non-degenerate then • so this ket is also an eigenvector of B • If a is degenerate then • Thereby, if A and B commute, each eigensubspace of A is globally invariant (stable) under the action of B

Observables • If • Then • If two operators commute, there is an orthonormal basis with eigenvectors common to both operators 2. D. 3

Observables 2. D. 3 • A set of observables, commuting by pairs, is called a complete set of commuting observables (CSCO) if there exists a unique orthonormal basis of common eigenvectors • If all the eigenvalues of a certain operator are nondegenerate, this operator constitutes CSCO by itself • If one ore more eigenvalues of a certain operator are degenerate, there is no unique orthonormal basis of eigenvectors • Then at least one more operator commuting with the first one is used to construct a unique orthonormal basis of common eigenvectors, an thus a CSCO

Examples of representations • Let us consider a set of functions: • The set is orthonormal: • Kets can be expanded: 2. E. 1

Examples of representations • Closure relation 2. E. 1

Examples of representations • For two kets • a scalar product is: 2. E. 1

Examples of representations • Let us consider a set of functions: • The set is orthonormal: • Kets can be expanded: 2. E. 1

Examples of representations • Closure relation 2. E. 1

Examples of representations • For two kets • a scalar product is: 2. E. 1

Change of representations • Recall: • Choosing • we obtain: 2. E. 1

R and P operators • For • we obtain: • where • Similarly • “Vector” operator R: 2. E. 2

R and P operators • “Vector” operator P: • Then: 2. E. 2

R and P operators • Analogously: • Then: 2. E. 2

R and P operators • Calculating a commutator: • Similarly: 2. E. 2

R and P operators • Calculating a matrix element: • Similarly: • Position and momentum operators are Hermitian 2. E. 2

R and P operators 2. E. 2 • Calculating a matrix element: • Thus: • Similarly: • Since |r > and |p > constitute complete bases, therefore operators R and P are observables • Sets of operators {X, Y, Z} as well as {Px, Py, Pz} comprise a CSCO each, however, separate operators don’t, since they are degenerate (in other directions)

Tensor products of state spaces 2. F. 1 • Spaces of square-integrable functions in 1 D, 2 D, and 3 D are not the same (e. g. , Er and Ex are different) • How are those spaces related? • In general, if there are two or more mutually isolated subsystems of a certain system, each of which has its own space, what is the space of the entire system? • Such questions are resolved via introduction of tensor products of spaces

Tensor products of state spaces 2. F. 2 • Let there be two spaces E 1 and E 2 with dimensions N 1 and N 2 • Tensor product of E 1 and E 2 is a vector field E with the following properties: • Notation: • If vectors belonging to E 1 and E 2 are • Then vectors belonging to E are • Tensor product is linear:

Tensor products of state spaces 2. F. 2 • Let there be two spaces E 1 and E 2 with dimensions N 1 and N 2 • Tensor product of E 1 and E 2 is a vector field E with the following properties: • Tensor product is distributive: • Tensor product of bases is a basis

Tensor products of state spaces 2. F. 2 • If: • Then: • Components of a tensor product of two vectors are products of the components • Not all the vectors in E can be represented as tensor products of vectors from E 1 and E 2:

Tensor products of state spaces • Scalar product: • For orthonormal bases: • Tensor product of operators: • Projector: 2. F. 2

Tensor products of state spaces • If: • Then: • And: • Eigenvectors of A(1) + B(2) are tensor products of eigenvectors of A(1) and eigenvectors of B(2) • If there is one CSCO in E 1 and another CSCO in E 2 their tensor product is a CSCO in E 2. F. 3

Tensor products of state spaces 2. F. 4 • If the problem is strictly 1 D (e. g. x-dependent), then the state space is Ex • In the x-representation the basis kets: • Similarly we can consider Ey and Ez: • Introducing • we get

Tensor products of state spaces 2. F. 4 • Exyz is the state space of a 3 D particle • A ket in 3 D can be represented: • In general, ψ cannot be factorized • Operator X in Ex is a CSCO by itself, but in Exyz its eigenvalues would be infinitely degenerate, because Ey and Ez in are infinitely-dimensional • On the other hand, the {X, Y, Z} set is a CSCO

States of a two-particle system • For two particles the state space is: • and the basis is: • A ket can be represented: • If: • Then: • In this case there is no correlation between the particles 2. F. 4