Chapter 2 Linear Relations and Functions Definitions DOMAIN

Chapter 2 Linear Relations and Functions

Definitions � DOMAIN: pairs � RANGE: pairs The set of x coordinates from a group of ordered The set of y coordinates from a group of ordered � FUNCTION: a type of relation in which each element of the domain is mapped with EXACTLY one element of the range � ONE-TO-ONE FUNCTION: each element of the range is paired with exactly one element of the domain � DISCRETE: a relation in which the domain is a set of individual points. � CONTINUOUS: a relation with an infinite number of elements and can be graphed continuously 2. 1 as a line or

State the Domain and Range. Is the relation a function? � Domain: (3, 3) (-3, 1) {-4, -3, 0, 1, 3} � Range: (1, 2) (-4, 0) (0, -2) {-2, 0, 1, 2, 3} � It is a function

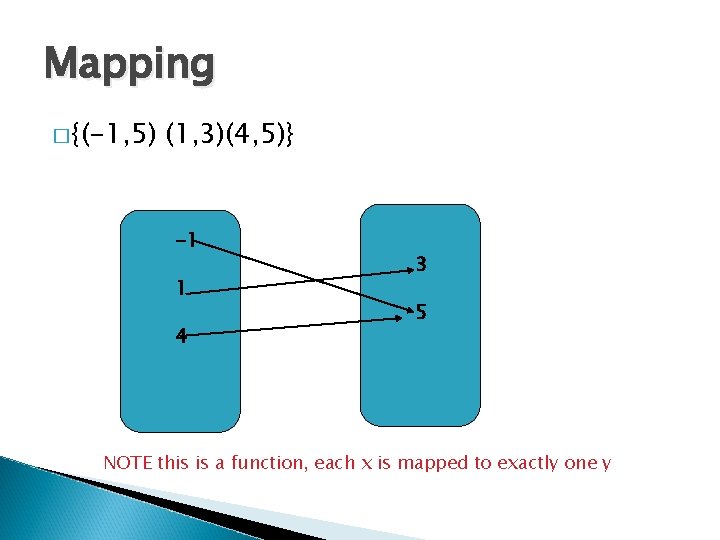
Mapping � {(-1, 5) (1, 3)(4, 5)} -1 1 4 3 5 NOTE this is a function, each x is mapped to exactly one y

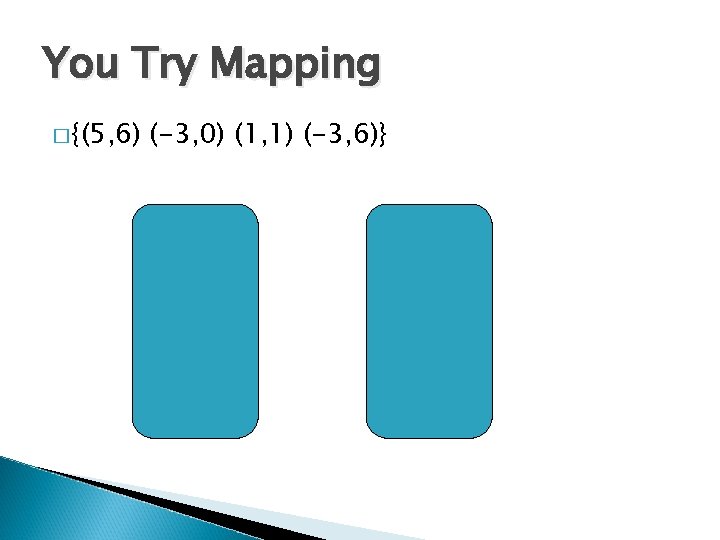
You Try Mapping � {(5, 6) (-3, 0) (1, 1) (-3, 6)}

Discrete vs. Continuous � Graph y=3 x-1 then find the domain and range, determine if it is discrete or continuous

Examples Continued � Graph y=x 2 + 1 and find the domain and range. Determine if it is discrete or continuous

Function Notation Substitute the variable with the term in the parentheses � Given f(x)= x 3 – 3 ◦ Find f(1) ◦ Find f(-2) ◦ Find f(2 y)

Linear Function f(x)=mx + b *Have a highest exponent of 1 o. Standard Form Ax + By = C Linear Equation y=mx+b *Have a highest exponent of 1 *A, B, and C must be integers 2. 2

Examples � 1. State whether each function is a linear function, explain. ◦ g(x)=2 x-5 �g(x) is a linear function because the highest exponent in 1 and it is in slope intercept form m=2 and b = -5 ◦ p(x)=x 3+2 �p(x) is not a linear function because x has an exponent > 1 ◦ f(x)= 4+7 x �f(x) is a linear function because the highest exponent is 1 and it can be written in slope intercept form with m=7 and b = 4

Example 2 Write each equation in standard form. Identify A, B, and C

Example 3 � Graph the equation by the intercepts. ◦ Find the x-int and y-int by substituting the other letter with a zero (write as ordered pairs) -2 x + y – 4 = 0

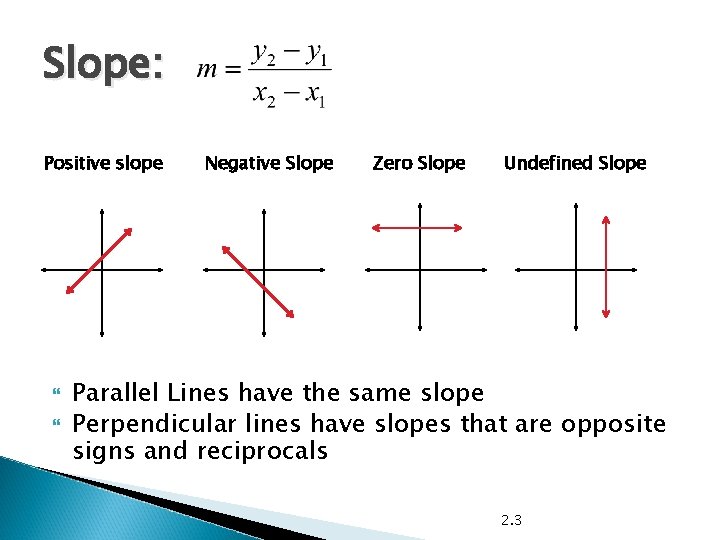
Slope: Positive slope Negative Slope Zero Slope Undefined Slope Parallel Lines have the same slope Perpendicular lines have slopes that are opposite signs and reciprocals 2. 3

Find the slope � A. (1, -3) (3, 5) � B. A line parallel to x – 3 y = 3 � C. A line perpendicular to (2, 2) (4, 2)

Graph the line � Passes x=4 � Passes through (2, -5) parallel to the graph of through the origin perpendicular to the graph of y = -x

Writing Linear Equations � Slope-Intercept Form: y = mx + b � m is slope and b is the y-intercept � Point-Slope Form: y – y 1 = m (x – x 1) �m is slope and y 1 and x 1 are any ordered pair on the line 2. 4

Write the equation of the line in slope-intercept and point-slope forms A. Through (6, 1) and (8, -4) B. Through (-5, 7) perpendicular to y = ½x + 6

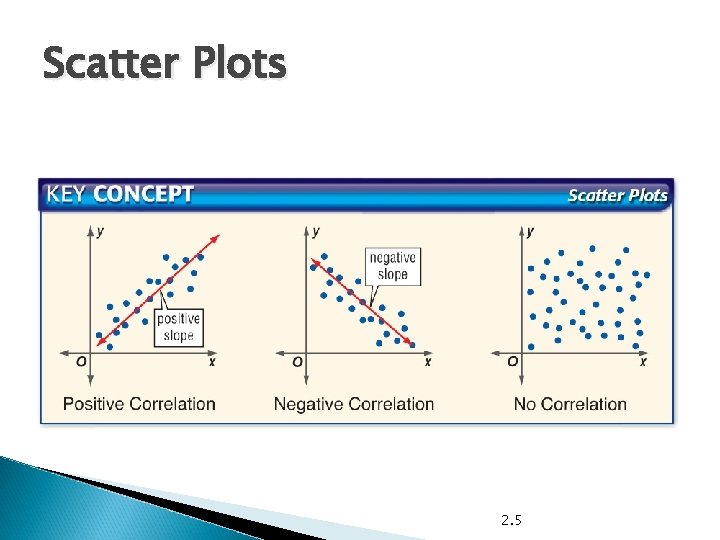
Scatter Plots 2. 5

Steps for Scatter Plots � Graph Ordered Pairs � Select two points to connect for the line of best fit. � Write equation of that line using those two points to find slope � Answer any additional questions using the equation you just wrote.

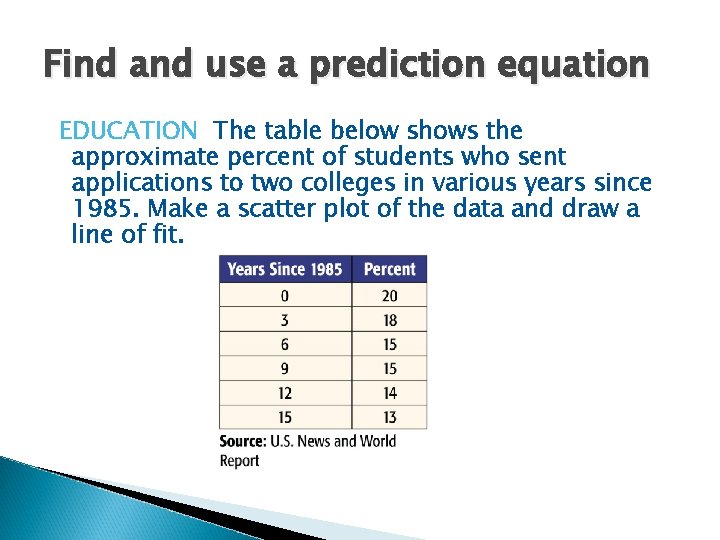
Find and use a prediction equation EDUCATION The table below shows the approximate percent of students who sent applications to two colleges in various years since 1985. Make a scatter plot of the data and draw a line of fit.

Answer Graph the data as ordered pairs, with the number of years since 1985 on the horizontal axis and the percentage on the vertical axis. The points (3, 18) and (15, 13) appear to represent the data well. Draw a line through these two points

Example 1 Cont… Find a prediction equation. What do the slope and yintercept indicate? � Find an equation of the line through (3, 18) and (15, 13). Begin by finding the slope Slope formula Substitute. Simplify.

Example 1 Cont… Point-slope form Substitute. Distribute. Simplify. Answer: One prediction equation is y = – 0. 42 x + 19. 26. The slope indicates that the percent of students sending applications to two colleges is falling about 0. 4% each year. The y-intercept indicates that the percent in 1985 should have been about 19%.

Example 1 Cont… � Predict the percent in 2010 � The year 2010 is 25 years after 1985, so use the prediction equation to find the value of y when x = 25. Prediction equation x = 25 Simplify. Answer: The model predicts that the percent in 2010 should be about 9%.

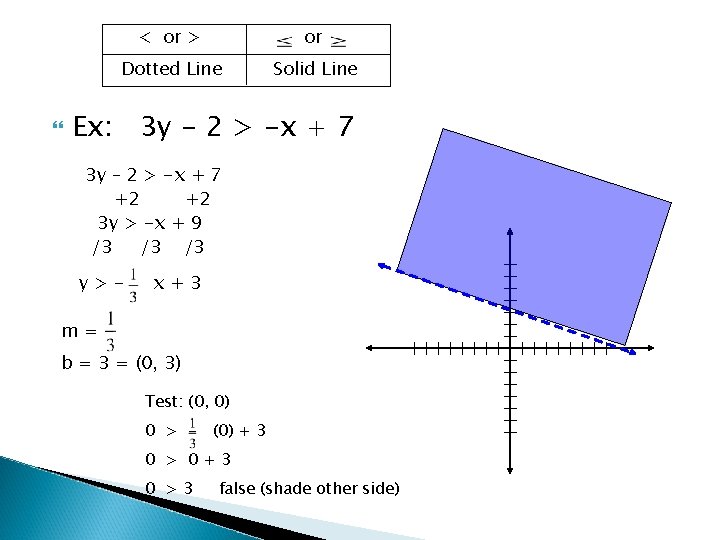
Graphing Inequalities • • 1. 2. 3. 4. The equation makes the line to define the boundary The shaded region is the half-plane Get the equation into slope-intercept form Graph the intercept and use the slope to find at least 2 more points Draw the line (dotted or solid) Test an ordered-pair not on the line 1. 2. If it is true shade that side of the line If it is false shade the other side of the line 2. 7

< or > or Dotted Line Solid Line Ex: 3 y - 2 > -x + 7 3 y – 2 > -x + 7 +2 +2 3 y > -x + 9 /3 /3 /3 y>- x+3 m=b = 3 = (0, 3) Test: (0, 0) 0 > - (0) + 3 0 > 0+3 0 >3 false (shade other side)