Chapter 2 Linear Programming Models Graphical and Computer

Chapter 2 Linear Programming Models: Graphical and Computer Methods

Outline • LP Meaning • LP Models • Model Formulation • Solving LP

LP Meaning • LP is a powerful quantitative tool used by the bp to obtain optimal solutions to problem that involve restrictions or limitations. • LP techniques consists of sequence of steps that will lead to an optimal solutions to linear-constrained problems. • LP involves the use of straight line relationships to maximize or minimise some functions usually called objective functions.

Properties of LP Models 1) Seek to minimize or maximize 2) Include “constraints” or limitations 3) There must be alternatives available 4) All equations are linear

LP models • LP models are mathematical representations of constrained optimization problems. • Four components provide the structure of a LP models i. iii. iv. Objective functions Decision variables Constraints Parameters

• Objective function: mathematical statement of profit(or cost) for a given solution • Decision variables: Amount of either inputs or outputs • Constraints: Limitations that restrict the available alternatives. 3 types of constraints ie <=, >= or=

Solving the LP: Outline of Graphical procedure i. Set up the objective function and the constraints in mathematical format ii. Plot the constraints iii. Identify the feasible solution space iv. Plot the objective function v. Determine the optimum solution

Steps in Developing a Linear Programming (LP) Model 1) Formulation 2) Solution 3) Interpretation and Sensitivity Analysis

Example LP Model Formulation: The Product Mix Problem Decision: How much to make of > 2 products? Objective: Maximize profit Constraints: Limited resources

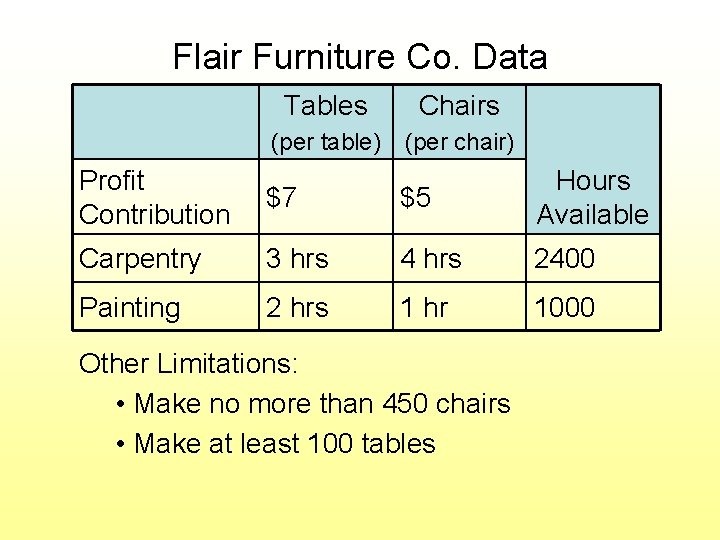
Example: Flair Furniture Co. Two products: Chairs and Tables Decision: How many of each to make this month? Objective: Maximize profit

Flair Furniture Co. Data Tables Chairs (per table) (per chair) Profit Contribution $7 $5 Hours Available Carpentry 3 hrs 4 hrs 2400 Painting 2 hrs 1 hr 1000 Other Limitations: • Make no more than 450 chairs • Make at least 100 tables

Decision Variables: T = Num. of tables to make C = Num. of chairs to make Objective Function: Maximize Profit Maximize $7 T + $5 C

Constraints: • Have 2400 hours of carpentry time available 3 T + 4 C < 2400 (hours) • Have 1000 hours of painting time available 2 T + 1 C < 1000 (hours) Nonnegativity: Cannot make a negative number of chairs or tables T>0 C>0

Model Summary Max 7 T + 5 C (profit) Subject to the constraints: 3 T + 4 C < 2400 (carpentry hrs) 2 T + 1 C < 1000 (painting hrs) T, C > 0 (nonnegativity)

Graphical Solution • Graphing an LP model helps provide insight into LP models and their solutions. • While this can only be done in two dimensions, the same properties apply to all LP models and solutions.

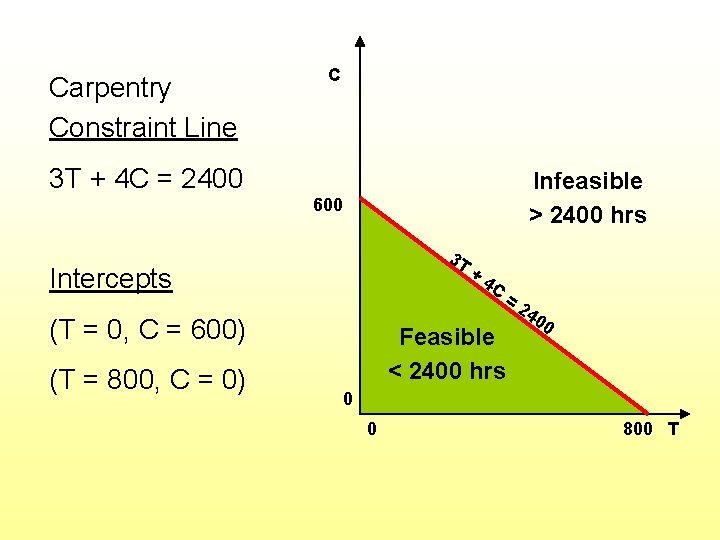
Carpentry Constraint Line C 3 T + 4 C = 2400 Infeasible > 2400 hrs 600 3 T Intercepts (T = 0, C = 600) (T = 800, C = 0) + 4 C = Feasible < 2400 hrs 24 00 0 0 800 T

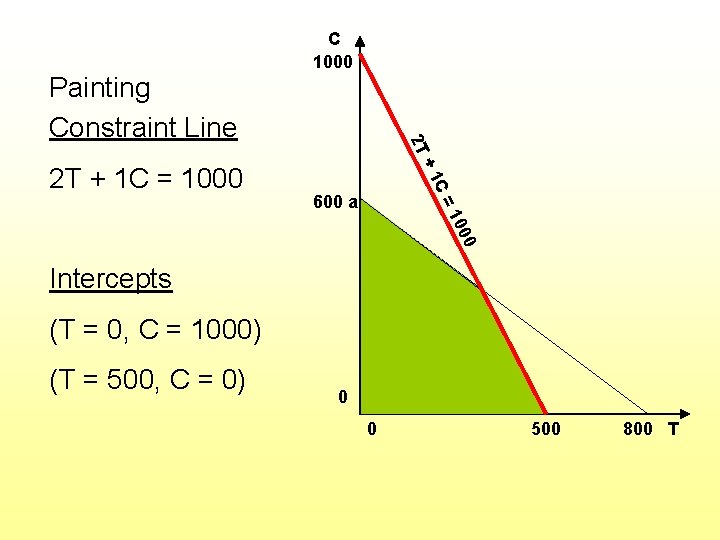
C= +1 2 T + 1 C = 1000 2 T Painting Constraint Line C 1000 600 a 00 10 Intercepts (T = 0, C = 1000) (T = 500, C = 0) 0 0 500 800 T

Corner point solution • Value of Z at corner point a • Z= 7 T+5 C • Za =7. 0+5*600 • Za=3000 • Value of Z at d • Z=7 T+5 C • Zd=7*500+5*0=3500

• Value of Z at b • Z=7 T+5 C • Use simultaneous equation • (1) 3 T + 4 C =2400 (carpentry hrs) • (2) 2 T + 1 C = 1000(painting hrs) • Multiply equation 2 by 4 • • (3) 8 T+4 C =4000 1 -3= -5 T= -1600 T= 320 now substitute the value of T in any equation 2*320+ 1 C=1000 1 C= 1000 -640 C= 360 Z= 7*320+5*360=4040

LP Characteristics • Feasible Region: The set of points that satisfies all constraints • Corner Point Property: An optimal solution must lie at one or more corner points • Optimal Solution: The corner point with the best objective function value is optimal

Special Situation in LP 1. Redundant Constraints - do not affect the feasible region Example: x < 10 x < 12 The second constraint is redundant because it is less restrictive.

Problem-1 • A frim can produce two types of a certain product, namely basic B and deluxe. D. The estimated profit per unit is $10 Basic and $15 Deluxe. The firm has 60 hours of labour available per day and 100 units of capital. Each unit of basic product B requires two hrs of labor and four units of capital. Each unit de-luxe product D requires four hrs of labor and five units of capital. How much of each type of product should the firm produce in order to maximise total profit?

Model Summary • Maximise Z= 10 B+15 D …objective function • Subject to: • 2 B+4 D<= 60… labour constraint • 4 B+5 D<=100. . . Capital constraint • B>=0, D>= non-negative constraints

Plotting the constraints • The labour constraint line: if we use all our 60 hrs of labor on the basic B we can produce 30 units of B but zero D. At the other extreme if use all our labor to produce D we can produce 15 D but Zero B • The capital Constraint line same way we can get B= 25 and D=20

• • • Identify the feasible solution space Feasible region of production area OVWX Value of Z at corner point V Zv=10 B+15 D=10*25+15*0=250 Value of Z at corner point X Zx=10*0+15*5=225 Value of Z at corner point W (1)2 B+4 D=60 (2)4 B+5 D=100 Here multiply equation 1 by 2 and subtract the equation 4 B+8 D=120 4 B+5 D=100 3 D= 20/3 then substitute D & get the Value of B=16 2/3 and we can solve for Z at W= 266 2/3

Problem 2 • A firm uses three types of factor input, namely labour, capital and raw material in producing two products X and Y. Each unit of X contributes $20 to profit, each unit of Y contributes $30 to profit. To produce one unit of X requires one unit of labour, one unit of capital and two units of raw material. To produce one unit of Y requires one unit of labour, two units of capital and one unit of raw material. The firm has 50 units of labour, 80 units of capital and 80 units of raw material available. How much of each type of product should the firm produce in order to maximise total profit?

Minimisation Problem-3 • A travel company operates two types of vehicle A and B. Vehicle A can carry 40 passengers and 30 tons of baggage; Vehicle B can carry 60 passengers but only 15 tons of baggage. The travel company is contracted to carry at least 960 passengers and 360 tons of baggage per journey. If vehicle A cost $1000 to operate per journey and vehicle B costs $1200 to operate per journey. What choice of vehicles will minimise the total cost

• • • Minimise Z= 1000 A+1200 B Subject to 40 A+60 B>= 960…Passengers constraint 30 A+15 B>=360…baggage constraint A>=0, B>=0… non negative constraints

Using Excel’s Solver for LP Recall the Flair Furniture Example: Max 7 T + 5 C (profit) Subject to the constraints: 3 T + 4 C < 2400 (carpentry hrs) 2 T + 1 C < 1000 (painting hrs) C < 450 (max # chairs) T > 100 (min # tables) T, C > 0 (nonnegativity) Go to file 2 -1. xls