CHAPTER 2 LINEAR EQUATIONS AND FUNCTIONS BIG IDEAS

CHAPTER 2: LINEAR EQUATIONS AND FUNCTIONS BIG IDEAS: 1. Representing relations and functions 2. Graphing linear equations and inequalities in two variables 3. Writing linear equations and inequalities in two variables

On a blank notebook page, please complete the Prerequisite Skills on PG 70 #2 -12 Even

LESSON 1: REPRESENT RELATIONS AND FUNCTIONS

ESSENTIAL QUESTION How do you graph relations and functions?

VOCABULARY • Relation: A mapping, or pairing, of input values with output values • Domain: The set of input values of a relation • Range: The set of output values of a relation • Function: A relation for which each input has exactly one output

Represent relations EXAMPLE 1 Consider the relation given by the ordered pair 1), (1, 3), (2, – 2), and (3, 1). a. (– 2, – 3), (– 1, Identify the domain and range. SOLUTION The domain consists of – 2, – 1, 1, 2, and 3. The range consists of all the y-coordinates: – 3, – 2, 1, and 3. all the x-coordinates:

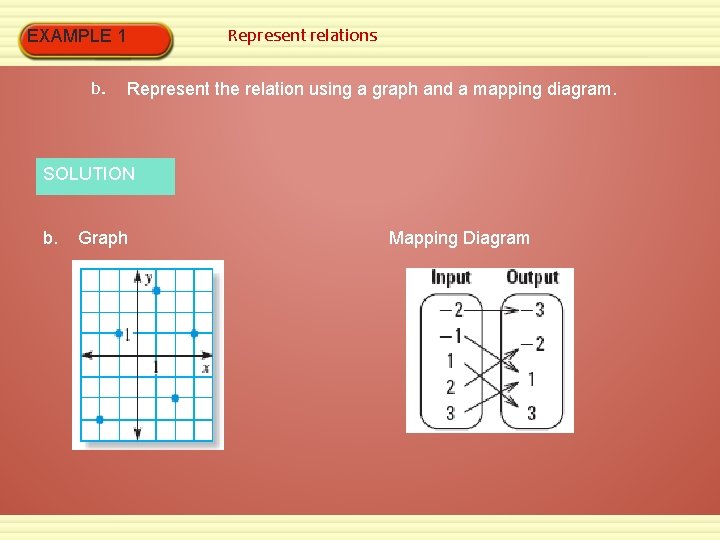
EXAMPLE 1 b. Represent relations Represent the relation using a graph and a mapping diagram. SOLUTION b. Graph Mapping Diagram

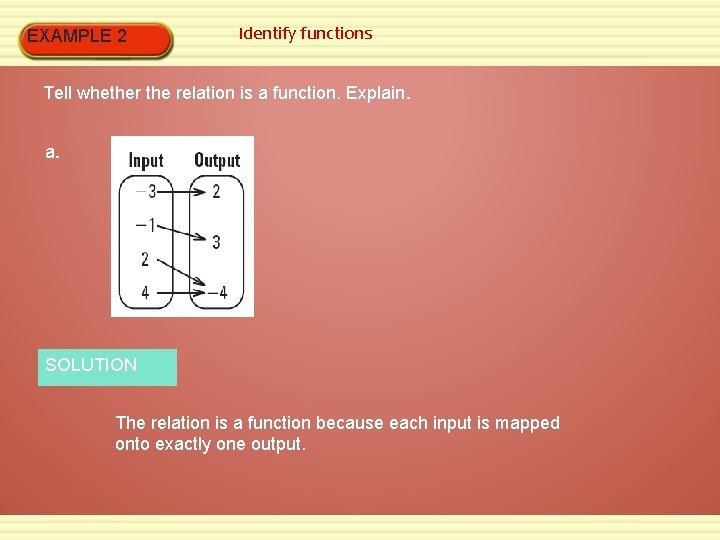
EXAMPLE 2 Identify functions Tell whether the relation is a function. Explain. a. SOLUTION The relation is a function because each input is mapped onto exactly one output.

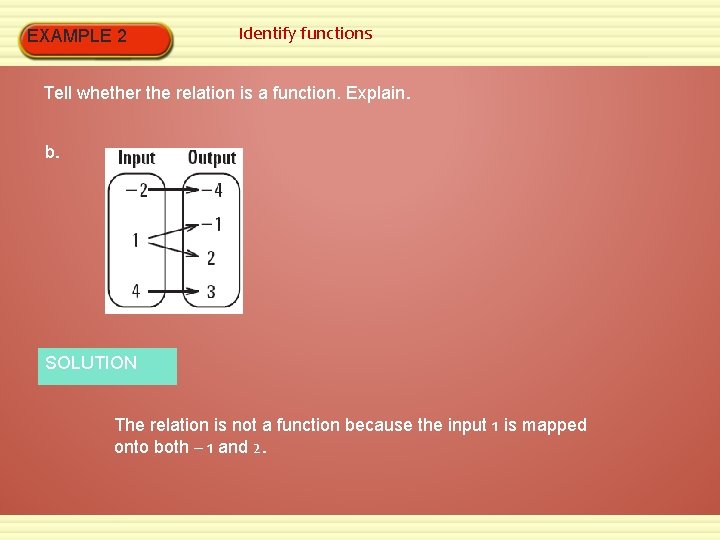
EXAMPLE 2 Identify functions Tell whether the relation is a function. Explain. b. SOLUTION The relation is not a function because the input 1 is mapped onto both – 1 and 2.

GUIDED PRACTICE for Examples 1 and 2 1. Consider the relation given by the ordered pairs (0, 3), (1, – 2), and (– 2, – 4) a. (– 4, 3), (– 2, 1), Identify the domain and range. SOLUTION The domain consists of all the x-coordinates: – 4, – 2, 0 and 1, The range consists of all the y-coordinates: 3, 1, – 2 and – 4

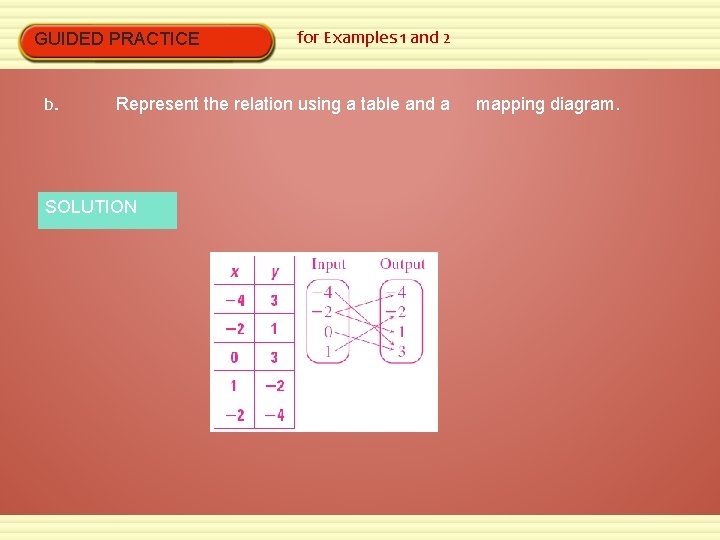
GUIDED PRACTICE b. for Examples 1 and 2 Represent the relation using a table and a SOLUTION mapping diagram.

GUIDED PRACTICE 2. for Examples 1 and 2 Tell whether the relation is a function. Explain. ANSWER Yes; each input has exactly one output.

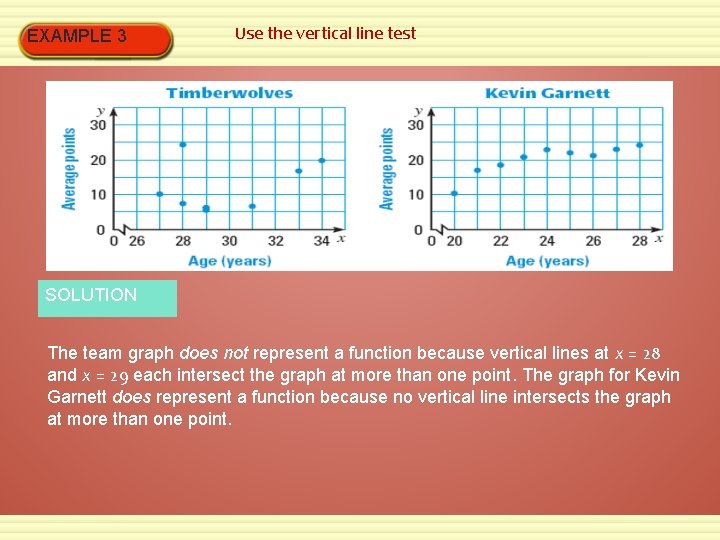
EXAMPLE 3 Use the vertical line test SOLUTION The team graph does not represent a function because vertical lines at x = 28 and x = 29 each intersect the graph at more than one point. The graph for Kevin Garnett does represent a function because no vertical line intersects the graph at more than one point.

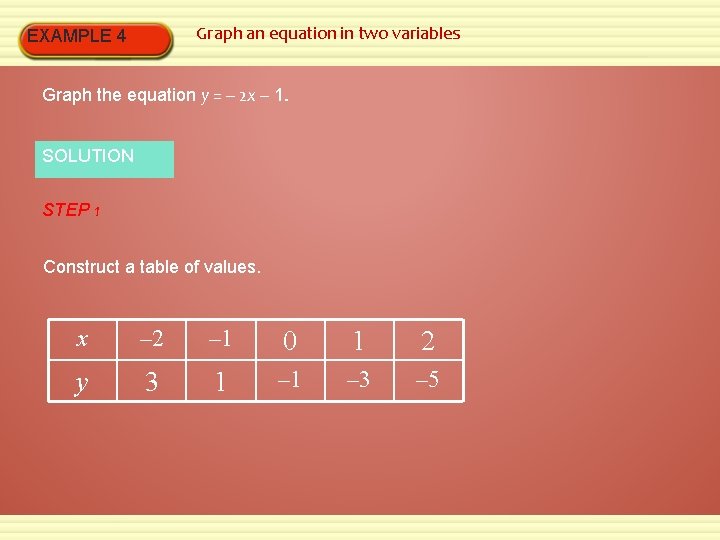
Graph an equation in two variables EXAMPLE 4 Graph the equation y = – 2 x – 1. SOLUTION STEP 1 Construct a table of values. x – 2 – 1 0 1 2 y 3 1 – 3 – 5

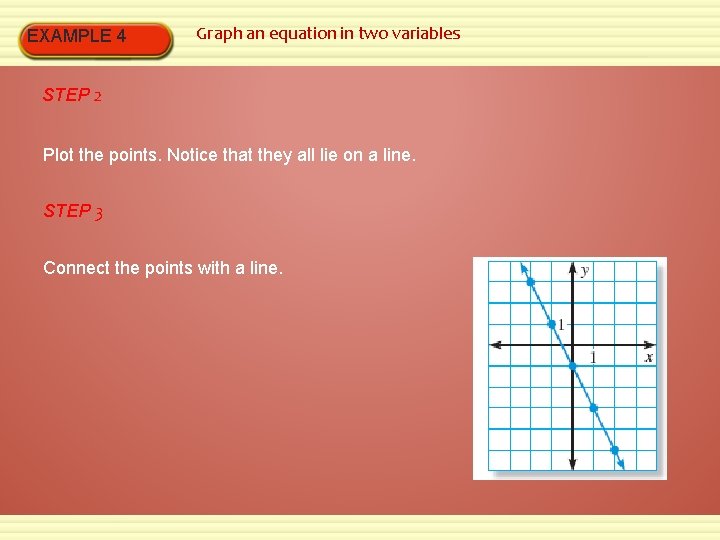
EXAMPLE 4 Graph an equation in two variables STEP 2 Plot the points. Notice that they all lie on a line. STEP 3 Connect the points with a line.

Classify and evaluate functions EXAMPLE 5 Tell whether the function is linear. Then evaluate the function when x = – 4. a. f (x) = –x 2 – 2 x + 7 SOLUTION The function f is not linear because it has an x 2 -term. f (x) = –x 2 – 2 x + 7 f (– 4) = –(– 4)2 – 2(– 4) + 7 = – 1 Write function. Substitute – 4 for x. Simplify.

Classify and evaluate functions EXAMPLE 5 b. g(x) = 5 x + 8 SOLUTION The function g is linear because it has the form g(x) = mx + b. g(x) = 5 x + 8 g(– 4) = 5(– 4) + 8 = – 12 Write function. Substitute – 4 for x. Simplify.

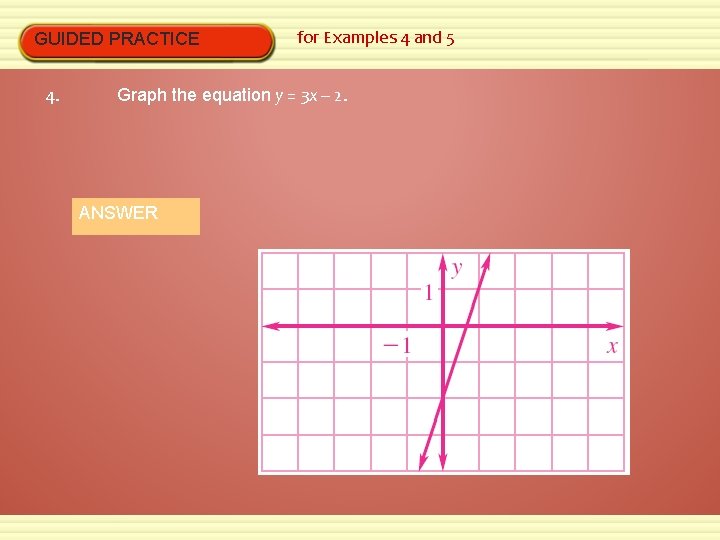
GUIDED PRACTICE 4. for Examples 4 and 5 Graph the equation y = 3 x – 2. ANSWER

GUIDED PRACTICE for Examples 4 and 5 Tell whether the function is linear. Then evaluate the function when x = – 2. 5. f (x) = x – 1 – x 3 6. g (x) = – 4 – 2 x ANSWER Not Linear; The f(x) = 5, when x = – 2 The f(x) = 0, when x = – 2

ESSENTIAL QUESTION How do you graph relations and functions? Make a table of domain and range values. Then plot the points from the table. If it is a function, connect the dots.

An internet company had a profit of $2. 6 million in retail sales over the last five years. What was its average annual profit?

LESSON 2: FIND SLOPE AND RATE OF CHANGE

ESSENTIAL QUESTION How do you determine whether two nonvertical lines are parallel or perpendicular?

VOCABULARY • Slope: The ratio of vertical change (the rise) to the horizontal change (the run) for a nonvertical line • Parallel: Two lines in the same plane that do not intersect • Perpendicular: Two lines in the same plane that intersect to form a right angle • Rate of change: A comparison of how much one quantity changes, on average, relative to the change in another quantity.

EXAMPLE 1 Find slope in real life Skateboarding A skateboard ramp has a rise of 15 inches and a run of 54 inches. What is its slope? SOLUTION slope = rise = 15 = 5 run 54 18 ANSWER The slope of the ramp is 5. 18

EXAMPLE 2 Standardized Test Practice SOLUTION Let (x 1, y 1) = (– 1, 3) and (x 2, y 2) = (2, – 1). y 2 – y 1 m= x –x 2 1 – 3 4 = 2 – (– 1) = 3 ANSWER The correct answer is A.

GUIDED PRACTICE 2. for Examples 1 and 2 What is the slope of the line passing through the points (– 4, 9) and (– 8, 3) ? ANSWER The correct answer is D.

for Examples 1 and 2 GUIDED PRACTICE Find the slope of the line passing through the given points. 3. (0, 3), (4, 8) ANSWER 4. 5. 5 4 (– 5, 1), (5, – 4) ANSWER 6. – 1 2 (– 3, – 2), (6, 1) 1 3 (7, 3), (– 1, 7) ANSWER – 1 2

EXAMPLE 4 Classify parallel and perpendicular lines Tell whether the lines are parallel, perpendicular, or neither. a. Line 1: through (– 2, 2) and (0, – 1) b. Line 1: through (1, 2) and (4, – 3) Line 2: through (– 4, – 1) and (2, 3) Line 2: through (– 4, 3) and (– 1, – 2) SOLUTION a. m 1 = Find the slopes of the two lines. – 1 – 2 0 – (– 2) = – 3 2

for Example 4 GUIDED PRACTICE Tell whether the lines are parallel, perpendicular, or neither. 11. Line 1: through (– 2, 8) and (2, – 4) Line 2: through (– 5, 1) and (– 2, 2) ANSWER 12. perpendicular Line 1: through (– 4, – 2) and (1, 7) Line 2: through (– 1, – 4) and (3, 5) ANSWER neither

ESSENTIAL QUESTION How do you determine whether two nonvertical lines are parallel or perpendicular? Calculate the slope: • Parallel lines have equal slope • Perpendicular lines have slopes that are opposite reciprocals

In 2005, Carey’s Pet Shop had a profit of $55, 500. In 2006, profits were $38, 700. In a graph of the data, is the slope of the segment between 2005 and 2006 positive or negative?

LESSON 3: GRAPH EQUATIONS OF LINES

ESSENTIAL QUESTION How do you graph a linear equation using intercepts?

VOCABULARY • Y-intercept: The y-coordinate of a point where a graph intersects the yaxis • X-intercept: The x-coordinate of a point where a graph intersects the xaxis • Slope-intercept form: y=mx+b • Standard form: Ax + By = C where a ≠ 0

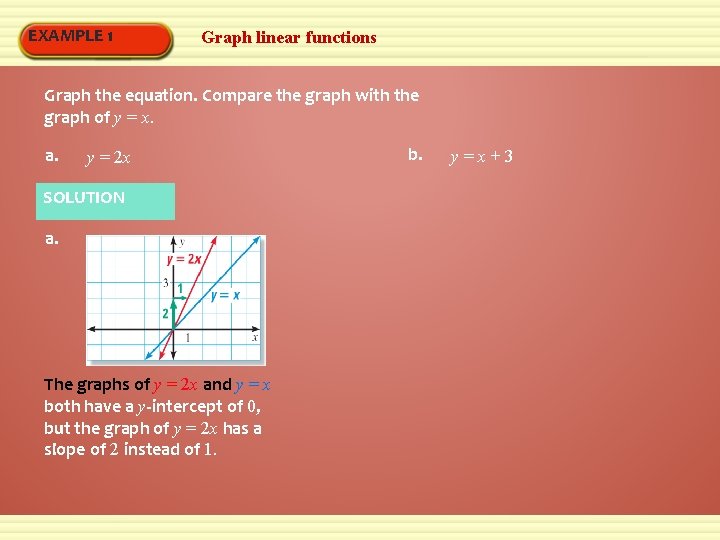
EXAMPLE 1 Graph linear functions Graph the equation. Compare the graph with the graph of y = x. a. y = 2 x SOLUTION a. The graphs of y = 2 x and y = x both have a y-intercept of 0, but the graph of y = 2 x has a slope of 2 instead of 1. b. y=x+3

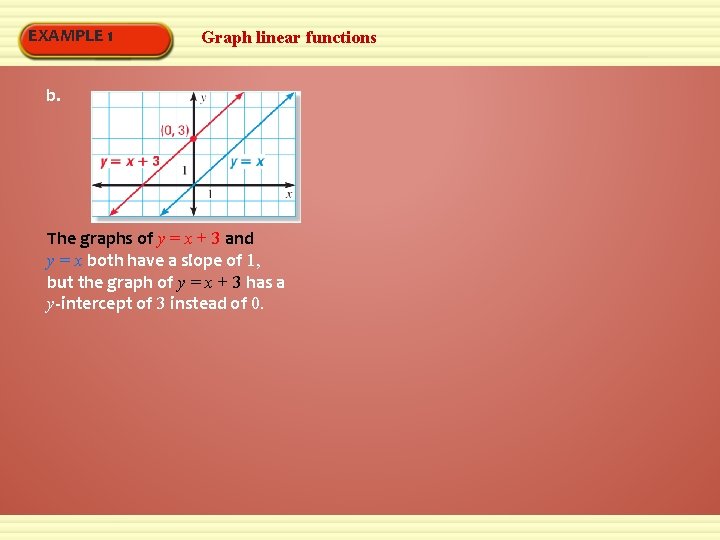
EXAMPLE 1 Graph linear functions b. The graphs of y = x + 3 and y = x both have a slope of 1, but the graph of y = x + 3 has a y-intercept of 3 instead of 0.

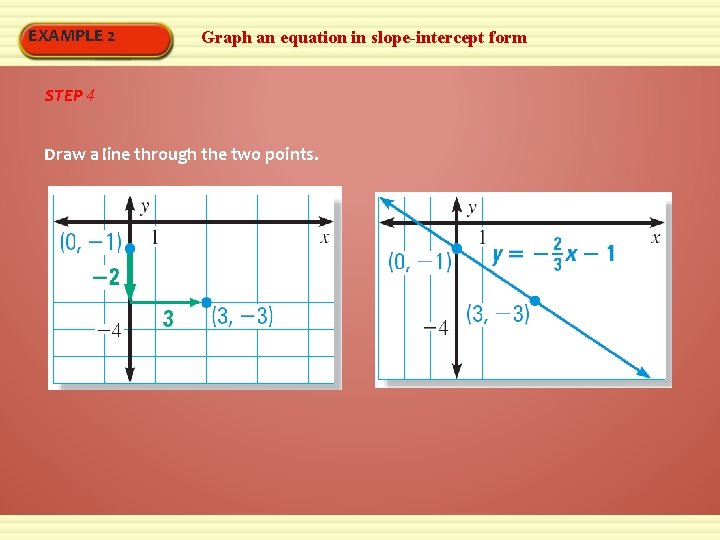
EXAMPLE 2 Graph an equation in slope-intercept form STEP 4 Draw a line through the two points.

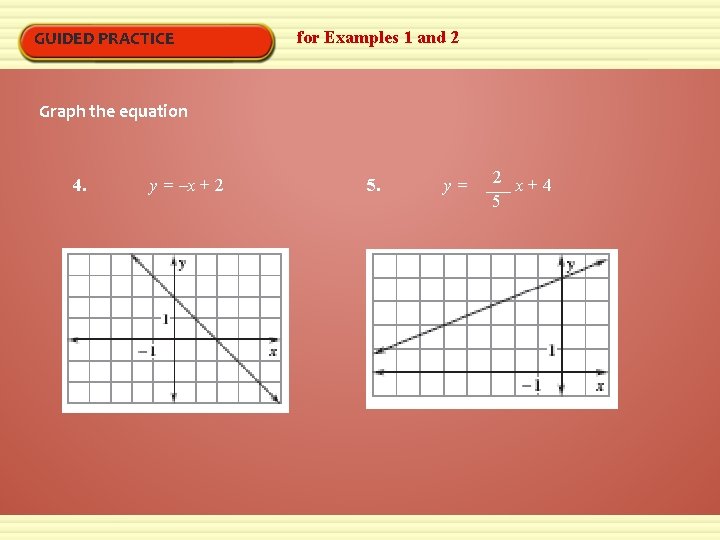
GUIDED PRACTICE for Examples 1 and 2 Graph the equation 4. y = –x + 2 5. y= 2 x+4 5

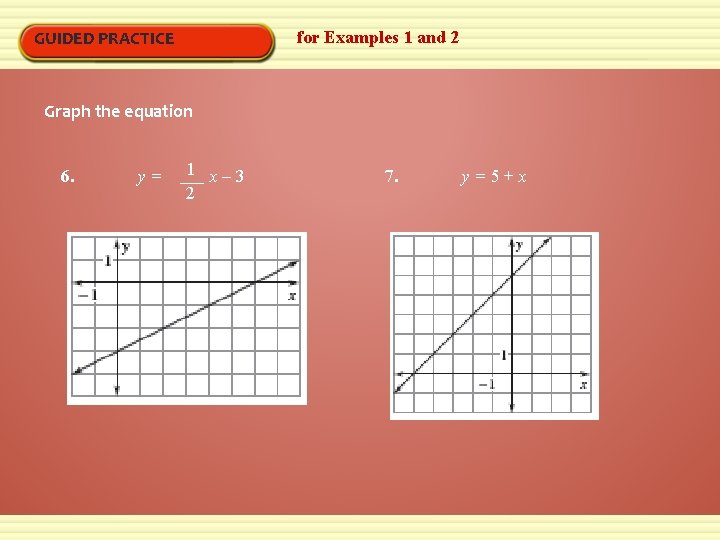
for Examples 1 and 2 GUIDED PRACTICE Graph the equation 6. y= 1 x– 3 2 7. y=5+x

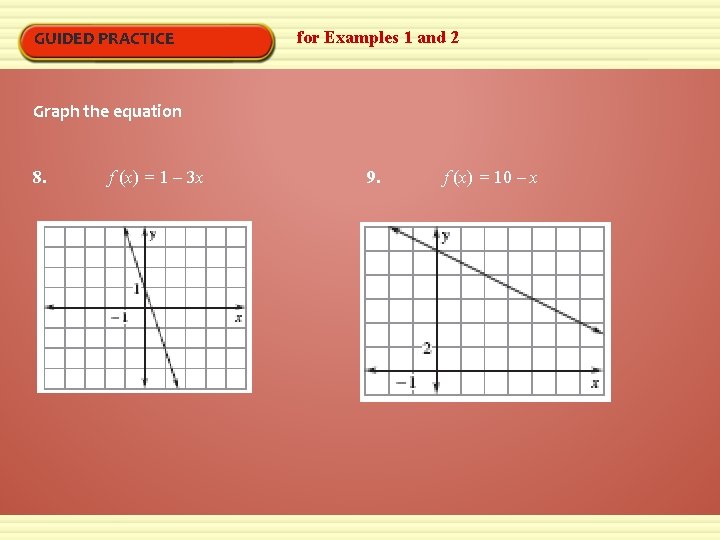
GUIDED PRACTICE for Examples 1 and 2 Graph the equation 8. f (x) = 1 – 3 x 9. f (x) = 10 – x

EXAMPLE 3 Solve a multi-step problem Biology The body length y (in inches) of a walrus calf can be modeled by y = 5 x + 42 where x is the calf’s age (in months). • Graph the equation. • Describe what the slope and y-intercept represent in this situation. • Use the graph to estimate the body length of a calf that is 10 months old.

EXAMPLE 3 Solve a multi-step problem SOLUTION STEP 1 Graph the equation. STEP 2 Interpret the slope and y-intercept. The slope, 5, represents the calf’s rate of growth in inches per month. The y-intercept, 42, represents a newborn calf’s body length in inches.

EXAMPLE 4 Graph an equation in standard form STEP 3 Identify the y-intercept. 5(0) + 2 y = 10 y=5 Let y = 0. Solve for y. The y-intercept is 5. So, plot the point (0, 5). STEP 4 Draw a line through the two points.

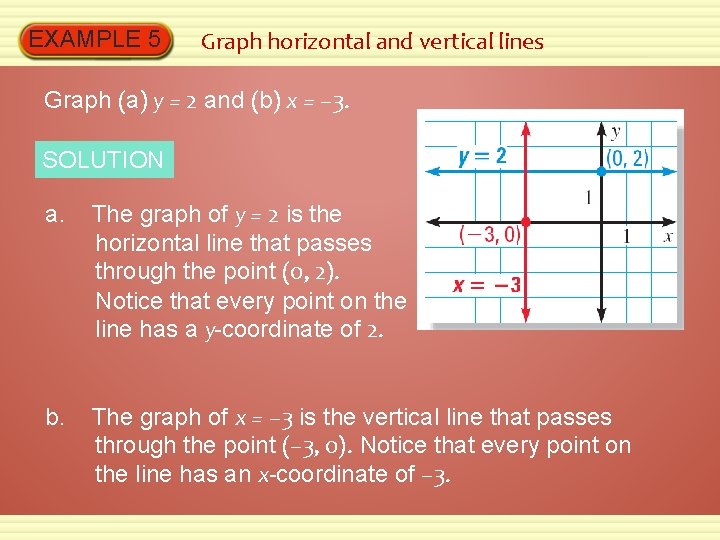
EXAMPLE 5 Graph horizontal and vertical lines Graph (a) y = 2 and (b) x = – 3. SOLUTION a. The graph of y = 2 is the horizontal line that passes through the point (0, 2). Notice that every point on the line has a y-coordinate of 2. b. The graph of x = – 3 is the vertical line that passes through the point (– 3, 0). Notice that every point on the line has an x-coordinate of – 3.

GUIDED PRACTICE for Examples 4 and 5 Graph the equation. 11. 2 x + 5 y = 10 12. 3 x – 2 y = 12

GUIDED PRACTICE for Examples 4 and 5 Graph the equation. 13. x = 1 14. y = – 4

ESSENTIAL QUESTION How do you graph a linear equation using intercepts? To find x: Set y = 0, solve for x, (x, 0) To find y: Set x = 0, solve for y, (0, y) Plot each intercept and connect the dots.

On a blank piece of paper please complete the Quiz for Lessons 2. 12. 3 on Page 96 #1 -9. When finished please turn into the homework bin.

LESSON 4: WRITE EQUATIONS OF LINES

ESSENTIAL QUESTION How do you write the equation of a line given the slope and a point?

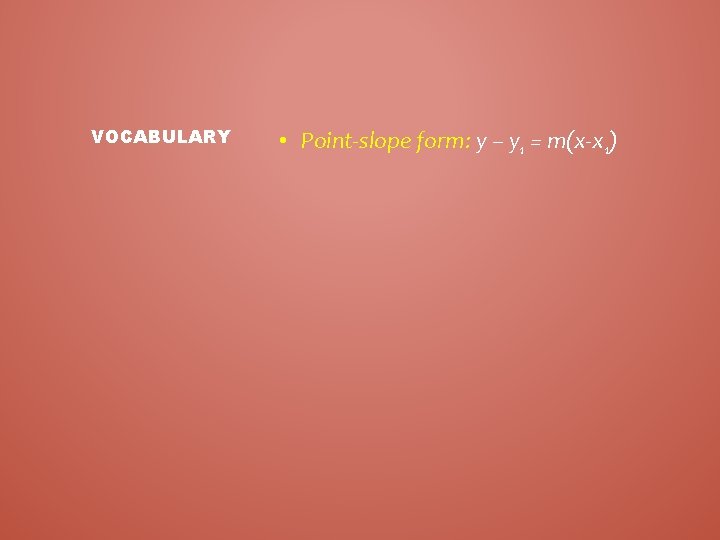
VOCABULARY • Point-slope form: y – y 1 = m(x-x 1)

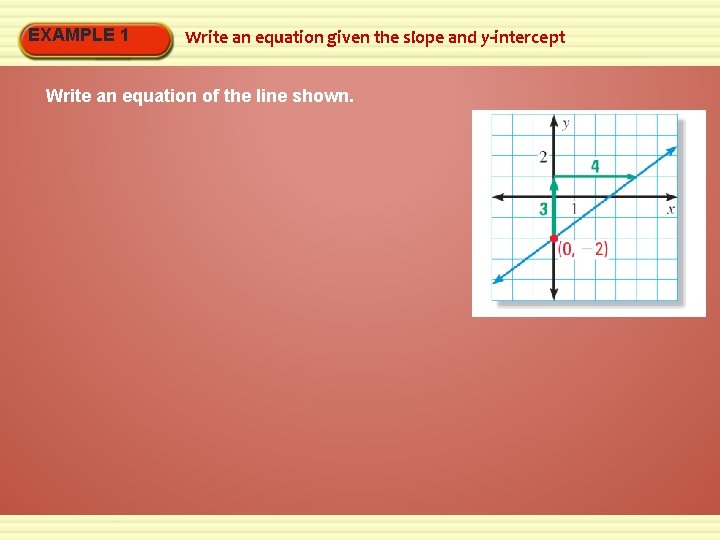
EXAMPLE 1 Write an equation given the slope and y-intercept Write an equation of the line shown.

GUIDED PRACTICE for Example 1 Write an equation of the line that has the given slope and y-intercept. 1. m = 3, b = 1 ANSWER y = x 3+ 1 2. m = – 2 , b = – 4 ANSWER y = – 2 x – 4 3. m = – 3 , b= 4 7 2 ANSWER y=– 3 x+ 4 7 2

EXAMPLE 2 Write an equation given the slope and a point Write an equation of the line that passes through (5, 4) and has a slope of – 3. SOLUTION Because you know the slope and a point on the line, use point-slope form to write an equation of the line. Let (x 1, y 1) = (5, 4) and m = – 3. y – y 1 = m(x – x 1) Use point-slope form. y – 4 = – 3(x – 5) Substitute for m, x 1, and y 1. y – 4 = – 3 x + 15 Distributive property y = – 3 x + 19 Write in slope-intercept form.

GUIDED PRACTICE 4. Write an equation of the line that passes through (– 1, 6) and has a slope of 4. ANSWER 5. for Examples 2 and 3 y = 4 x + 10 Write an equation of the line that passes through (4, – 2) and is (a) parallel to, and (b) perpendicular to, the line y = 3 x – 1. ANSWER y = 3 x – 14

EXAMPLE 4 Write an equation given two points Write an equation of the line that passes through (5, – 2) and (2, 10). SOLUTION The line passes through (x 1, y 1) = (5, – 2) and (x 2, y 2) = (2, 10). Find its slope. m= y 2 – y 1 x 2 – x 1 = 10 – (– 2) 2 – 5 = 12 – 3 = – 4

EXAMPLE 4 Write an equation given two points You know the slope and a point on the line, so use point-slope form with either given point to write an equation of the line. Choose (x 1, y 1) = (4, – 7). y 2 – y 1 = m(x – x 1) Use point-slope form. y – 10 = – 4(x – 2) Substitute for m, x 1, and y 1. y – 10 = – 4 x + 8 Distributive property y = – 4 x + 8 Write in slope-intercept form.

GUIDED PRACTICE for Examples 4 and 5 Write an equation of the line that passes through the given points. 6. (– 2, 5), (4, – 7) ANSWER y = – 2 x + 1 7. (6, 1), (– 3, – 8) ANSWER y=x– 5 8. (– 1, 2), (10, 0) ANSWER y= – 2 11 x+ 20 11

ESSENTIAL QUESTION How do you write the equation of a line given the slope and a point? 1. Plug m, x & y into the slope-intercept form: y = mx + b 2. Solve for b 3. Rewrite the equation with known m and b.

Write an equation of the line that passes through the points (0, 0) and (4, 8).

LESSON 5: MODEL DIRECT VARIATION

ESSENTIAL QUESTION What is a constant of variation?

VOCABULARY • Direct variation: Two variable x and y are this when y = ax where a is a nonzero constant • Constant of variation: The nonzero constant z in a direct variation, inverse variation or a joint variation

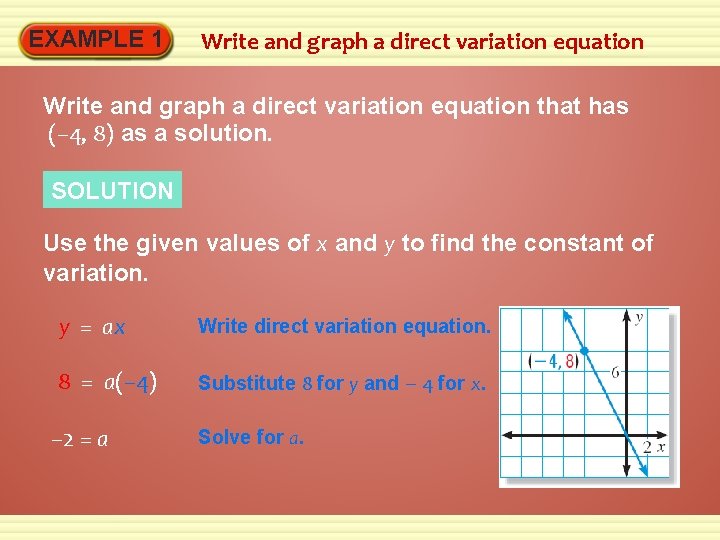
EXAMPLE 1 Write and graph a direct variation equation that has (– 4, 8) as a solution. SOLUTION Use the given values of x and y to find the constant of variation. y = ax Write direct variation equation. 8 = a(– 4) Substitute 8 for y and – 4 for x. – 2 = a Solve for a.

GUIDED PRACTICE for Example 1 Write and graph a direct variation equation that has the given ordered pair as a solution. 1. (3, – 9) ANSWER y = – 3 x.

GUIDED PRACTICE for Example 1 Write and graph a direct variation equation that has the given ordered pair as a solution. 2. (– 7, 4) ANSWER y =– 4 x 7

GUIDED PRACTICE for Example 1 Write and graph a direct variation equation that has the given ordered pair as a solution. 3. (5, 3) ANSWER y = 3 x 5

GUIDED PRACTICE for Example 1 Write and graph a direct variation equation that has the given ordered pair as a solution. 4. (6, – 2) ANSWER y =– 1 x 3

EXAMPLE 3 Use ratios to identify direct variation 215 1. 8 119 290 2. 4 121 350 2. 9 = 121 430 3. 6 119 565 4. 7 120 695 5. 8 120 ANSWER Because the ratios are approximately equal, the data show direct variation. An equation relating tooth length and body length is b = 120, or b = 120 t. t

ESSENTIAL QUESTION What is a constant of variation? - In the equation y = ax, a is the constant of variation - It represents the slope or rate of change of the direct variation equation

A line’s graph has slope 2/3 and contains the point (6, 1). Write the equation of the line.

LESSON 6: DRAW SCATTER PLOTS AND BEST-FITTING LINES

ESSENTIAL QUESTION How can you tell if a set of data points can be modeled by a best fitting line?

VOCABULARY • Scatter plot: A graph of a set of data pairs (x, y) used to determine whethere is a relationship between the variables x and y • Positive correlation: The paired data (x, y) are this way if y tends to increase as x increases (positive slope) • Negative correlation: The paired data (x, y) are this way if y tends to decrease as x increases (negative slope) • Best-fitting line: The line that lies as close as possible to all the data points in a scatter plot

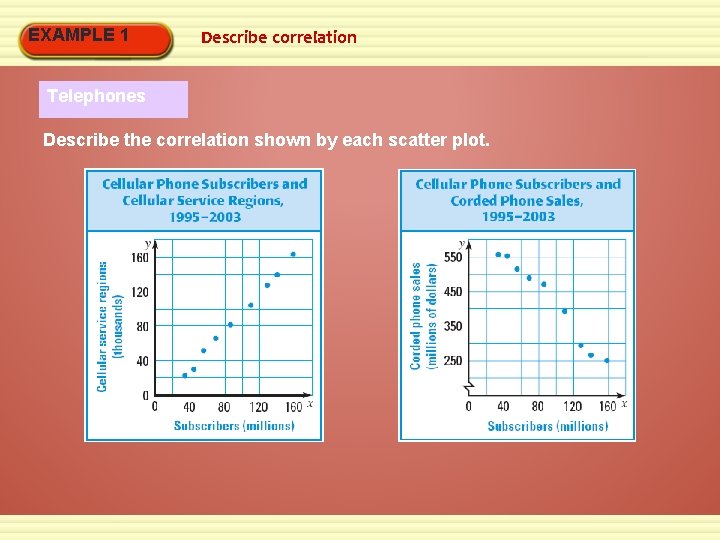
EXAMPLE 1 Describe correlation Telephones Describe the correlation shown by each scatter plot.

EXAMPLE 2 Estimate correlation coefficients Tell whether the correlation coefficient for the data is closest to – 1, – 0. 5, 0, 0. 5, or 1. a. SOLUTION a. The scatter plot shows a clear but fairly weak negative correlation. So, r is between 0 and – 1, but not too close to either one. The best estimate given is r = – 0. 5. (The actual value is r – 0. 46. )

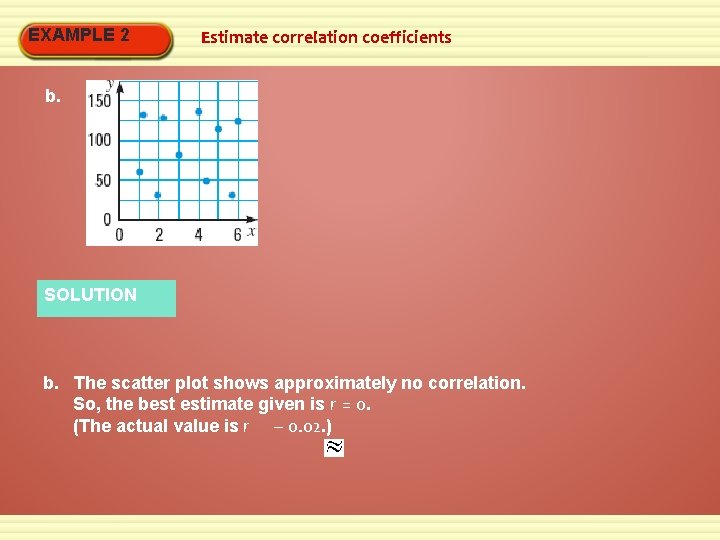
EXAMPLE 2 Estimate correlation coefficients b. SOLUTION b. The scatter plot shows approximately no correlation. So, the best estimate given is r = 0. (The actual value is r – 0. 02. )

EXAMPLE 2 Estimate correlation coefficients c. SOLUTION c. The scatter plot shows a strong positive correlation. So, the best estimate given is r = 1. (The actual value is r 0. 98. )

GUIDED PRACTICE for Examples 1 and 2 For each scatter plot, (a) tell whether the data have a positive correlation, a negative correlation, or approximately no correlation, and (b) tell whether the correlation coefficient is closest to – 1, – 0. 5, 0, 0. 5, or 1. ANSWER (a) positive correlation (b) r = 0. 5

GUIDED PRACTICE for Examples 1 and 2 For each scatter plot, (a) tell whether the data have a positive correlation, a negative correlation, or approximately no correlation, and (b) tell whether the correlation coefficient is closest to – 1, – 0. 5, 0, 0. 5, or 1. 2. ANSWER (a) negative correlation (b) r = – 1

GUIDED PRACTICE for Examples 1 and 2 For each scatter plot, (a) tell whether the data have a positive correlation, a negative correlation, or approximately no correlation, and (b) tell whether the correlation coefficient is closest to – 1, – 0. 5, 0, 0. 5, or 1. 3. ANSWER (a) no correlation (b) r = 0

EXAMPLE 3 Approximate a best-fitting line Use point-slope form to write the equation. Choose (x 1, y 1) = (1, 300). y – y 1 = m(x – x 1) y – 300 = 41. 3(x – 1) y 41. 3 x + 259 Point-slope form Substitute for m, x 1, and y 1. Simplify. ANSWER An approximation of the best-fitting line is y = 41. 3 x + 259.

EXAMPLE 4 Use a line of fit to make a prediction ANSWER You can predict that there will be about 796, 000 alternative-fueled vehicles in use in the United States in 2010.

GUIDED PRACTICE for Examples 3, 4 and 5 4. OIL PRODUCTION: The table shows the U. S. daily oil production y (in thousands of barrels) x years after 1994. a. Approximate the best-fitting line for the data. ANSWER y = – 130 x + 6710

GUIDED PRACTICE for Examples 3, 4 and 5 4. OIL PRODUCTION: The table shows the U. S. daily oil production y (in thousands of barrels) x years after 1994. b. Use your equation from part (a) to predict the daily oil production in 2009. ANSWER 4760 gal

GUIDED PRACTICE for Examples 3, 4 and 5 4. OIL PRODUCTION: The table shows the U. S. daily oil production y (in thousands of barrels) x years after 1994. c. Use a graphing calculator to find and graph an equation of the best-fitting line. Repeat the prediction from part (b) using this equation.

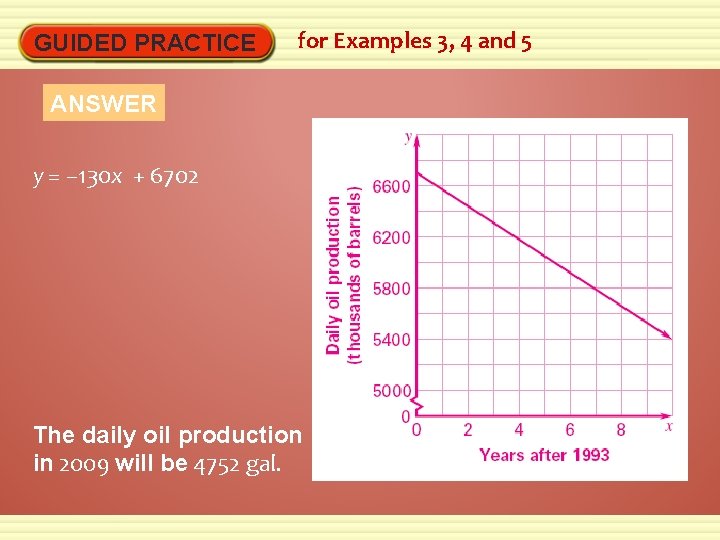
GUIDED PRACTICE for Examples 3, 4 and 5 ANSWER y = – 130 x + 6702 The daily oil production in 2009 will be 4752 gal.

ESSENTIAL QUESTION How can you tell if a set of data points can be modeled by a best fitting line? You can draw a line (either with negative or positive slope) with about as many points above it as are below it.

On a blank piece of paper please complete the Quiz for Lessons 2. 4 -2. 6 on Pg 120 #1 -15 ODD. Turn into the homework bin when finished.

LESSON 7: USE ABSOLUTE VALUE FUNCTIONS AND TRANSFORMATIO NS

ESSENTIAL QUESTION How do the values of a, h and k affect the graphing of y= a*f(x-h)+k in relation to the graph of y=f(x)

VOCABULARY • Absolute value function: A function that contains an absolute value expression • Transformation: changes a graph’s size, shape, position or orientation • Translation: A transformation that shifts a graph horizontally and/or vertically, but does not change its size, shape or orientation • Reflection: A transformation that flips a graph or figure in a line

EXAMPLE 1 Graph a function of the form y = | x – h | + k Graph y = | x + 4 | – 2. Compare the graph with the graph of y = | x |. SOLUTION STEP 1 Identify and plot the vertex, (h, k) = (– 4, – 2). STEP 2 Plot another point on the graph, such as (– 2, 0). Use symmetry to plot a third point, (– 6, 0).

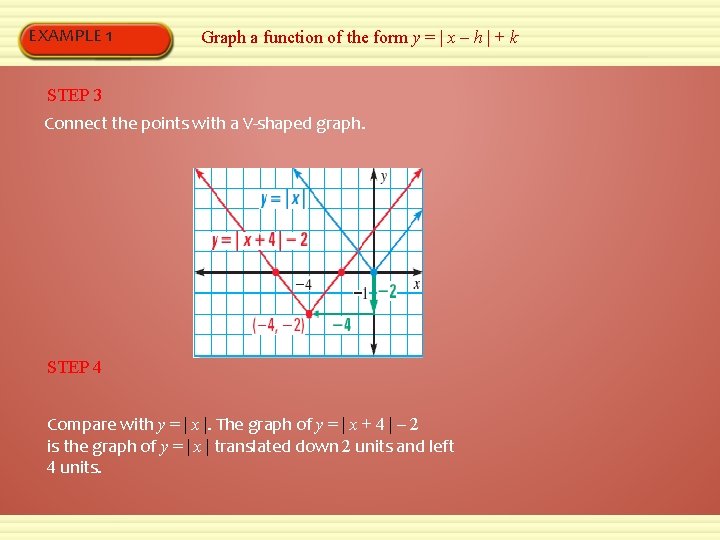
EXAMPLE 1 Graph a function of the form y = | x – h | + k STEP 3 Connect the points with a V-shaped graph. STEP 4 Compare with y = | x |. The graph of y = | x + 4 | – 2 is the graph of y = | x | translated down 2 units and left 4 units.

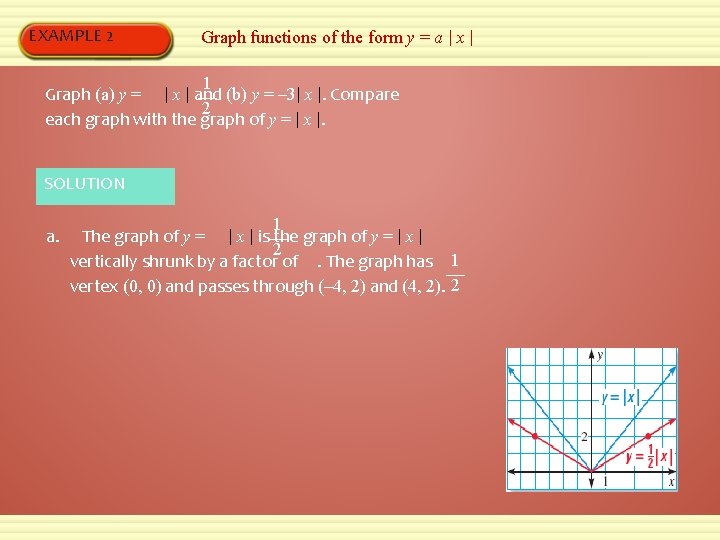
EXAMPLE 2 Graph functions of the form y = a | x | 1 Graph (a) y = | x | and (b) y = – 3| x |. Compare 2 each graph with the graph of y = | x |. SOLUTION a. 1 The graph of y = | x | is the graph of y = | x | 2 vertically shrunk by a factor of. The graph has 1 vertex (0, 0) and passes through (– 4, 2) and (4, 2). 2

EXAMPLE 2 b. Graph functions of the form y = a | x | The graph of y = – 3| x | is the graph of y = | x | vertically stretched by a factor of 3 and then reflected in the x-axis. The graph has vertex (0, 0) and passes through (– 1, – 3) and (1, – 3).

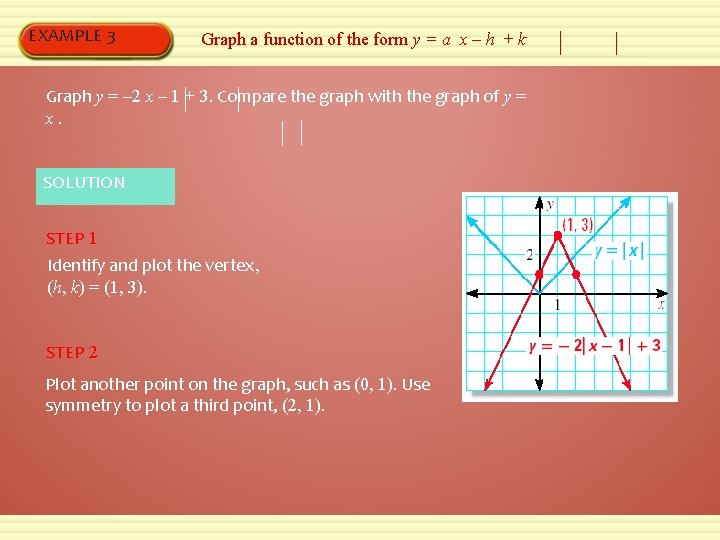
EXAMPLE 3 Graph a function of the form y = a x – h + k Graph y = – 2 x – 1 + 3. Compare the graph with the graph of y = x. SOLUTION STEP 1 Identify and plot the vertex, (h, k) = (1, 3). STEP 2 Plot another point on the graph, such as (0, 1). Use symmetry to plot a third point, (2, 1).

EXAMPLE 3 Graph a function of the form y = a x – h + k STEP 3 Connect the points with a V-shaped graph. STEP 4 Compare with y = x. The graph of y = – 2 x – 1 + 3 is the graph of y = x stretched vertically by a factor of 2, then reflected in the x-axis, and finally translated right 1 unit and up 3 units.

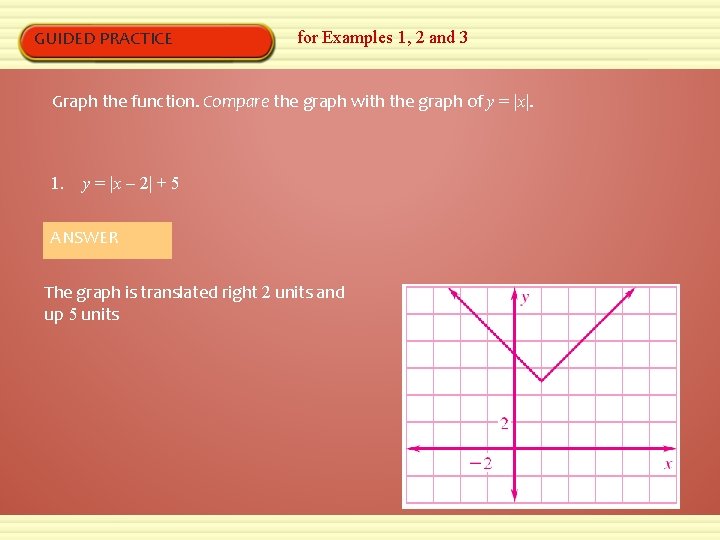
GUIDED PRACTICE for Examples 1, 2 and 3 Graph the function. Compare the graph with the graph of y = |x|. 1. y = |x – 2| + 5 ANSWER The graph is translated right 2 units and up 5 units

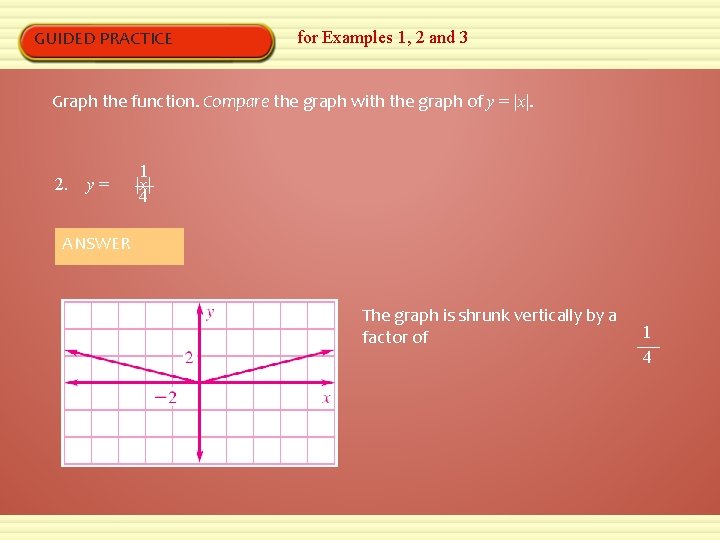
GUIDED PRACTICE for Examples 1, 2 and 3 Graph the function. Compare the graph with the graph of y = |x|. 2. y = 1 |x| 4 ANSWER The graph is shrunk vertically by a factor of 1 4

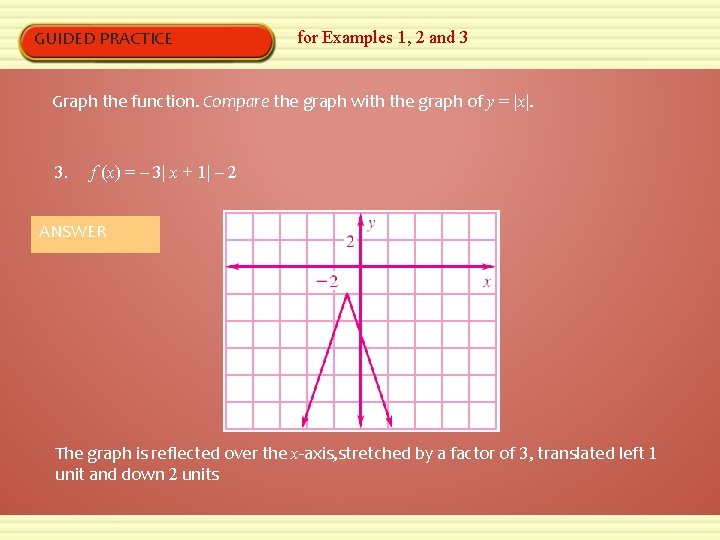
GUIDED PRACTICE for Examples 1, 2 and 3 Graph the function. Compare the graph with the graph of y = |x|. 3. f (x) = – 3| x + 1| – 2 ANSWER The graph is reflected over the x-axis, stretched by a factor of 3, translated left 1 unit and down 2 units

ESSENTIAL QUESTION How do the values of a, h and k affect the graphing of y= a*f(x-h)+k in relation to the graph of y=f(x) - When the absolute value of a is not equal to 1, the value of a causes a vertical shrink or stretch - If a = -1, the graph is reflected in the x-axis - H translates the graph horizontally - K translates the graph vertically

Tell whether each statement is true or false when x = -2 and y =1. a) 2 x-y <5 b) X + 3 y > 0

LESSON 8: GRAPH LINEAR INEQUALITIES IN TWO VARIABLES

ESSENTIAL QUESTION What does a dashed boundary line on the graph of an inequality represent?

VOCABULARY • Absolute value: the distance an umber is from 0 on a number line; always positive • Extraneous solution: an apparent solution that must be rejected because it does not satisfy the original equation

EXAMPLE 1 Standardized Test Practice SOLUTION Ordered pair Substitute (6, – 3) 3(6) + 4(– 3) = 6 > 8 (6, – 3) is not a solution (0, 2) is not a solution 3(0) + 4(2) = 8 > 8 (– 2, – 1) 3(– 2) + 4(– 1) = – 10 > 8 (– 3, 5) 3(– 3) + 4(5) = 11 > 8 Conclusion (– 2 , – 1) is not a solution (– 3, 5) is a solution

GUIDED PRACTICE for Example 1 Tell whether the given ordered pair is a solution of 5 x – 2 y ≤ 6. ANSWER Ordered pair Conclusion 1. (0, – 4) (0, – 4 ) is not a solution 2. (2, 2) (2, 2 ) is a solution 3. (– 3, 8) (– 3, 8 ) is a solution 4. (– 1, – 7) (– 1, – 7 ) is not a solution

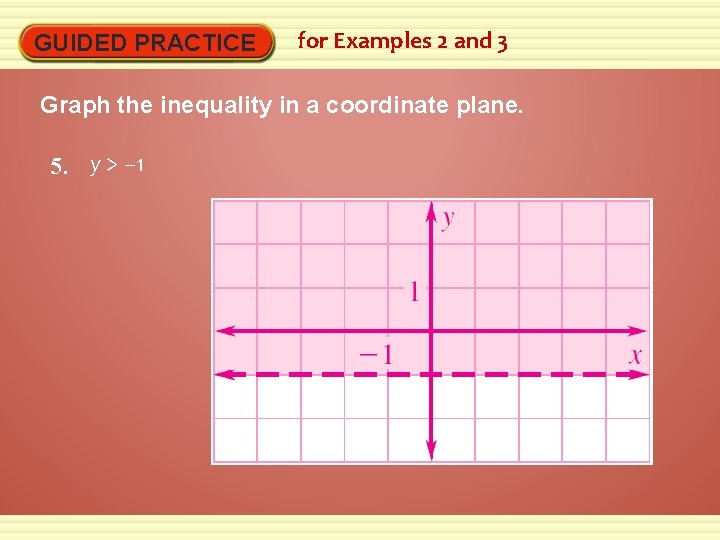
GUIDED PRACTICE for Examples 2 and 3 Graph the inequality in a coordinate plane. 5. y > – 1

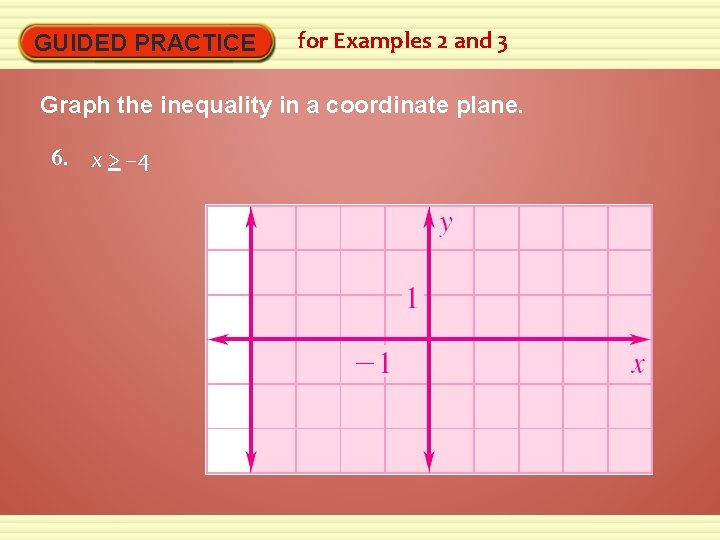
GUIDED PRACTICE for Examples 2 and 3 Graph the inequality in a coordinate plane. 6. x > – 4

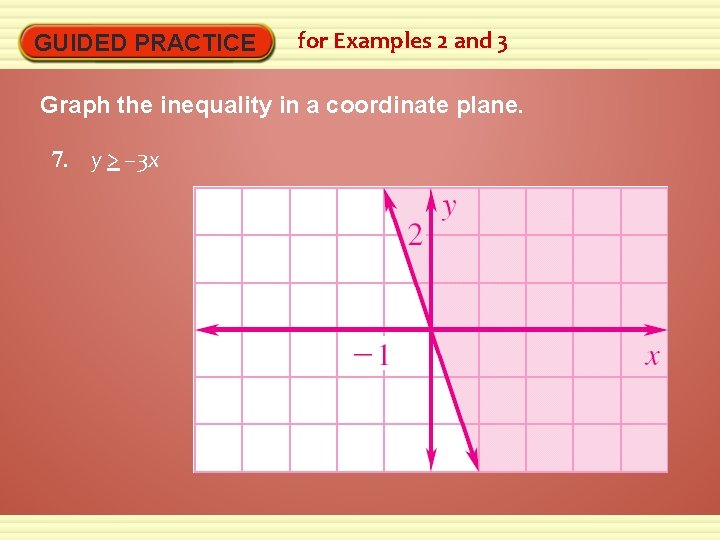
GUIDED PRACTICE for Examples 2 and 3 Graph the inequality in a coordinate plane. 7. y > – 3 x

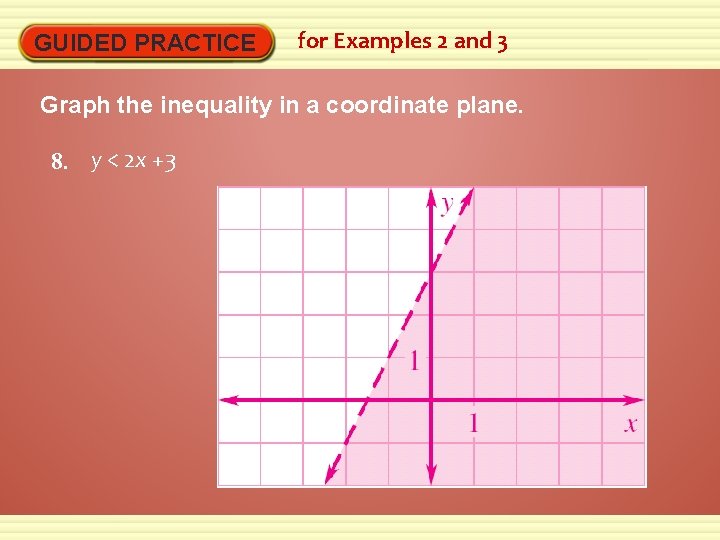
GUIDED PRACTICE for Examples 2 and 3 Graph the inequality in a coordinate plane. 8. y < 2 x +3

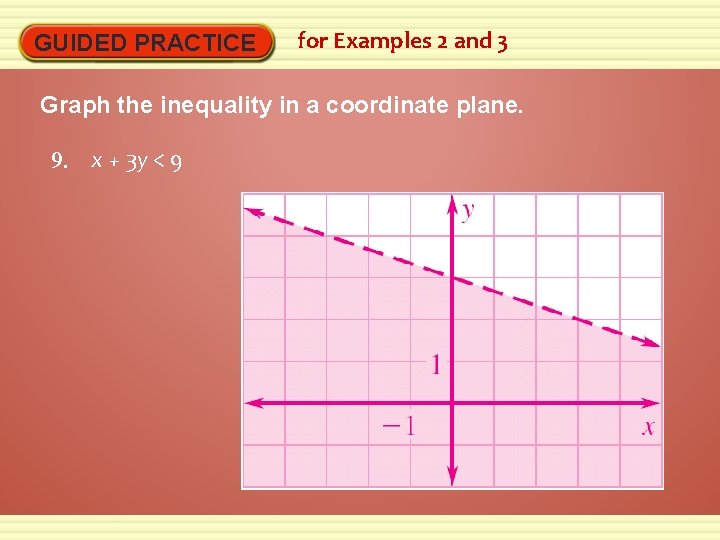
GUIDED PRACTICE for Examples 2 and 3 Graph the inequality in a coordinate plane. 9. x + 3 y < 9

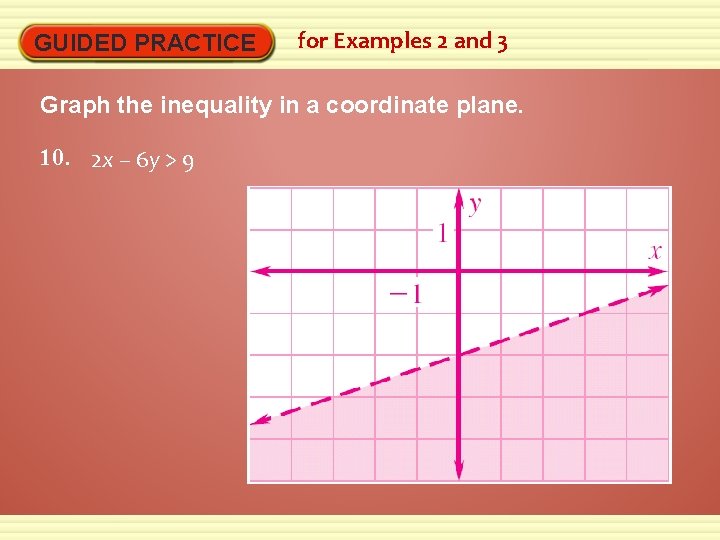
GUIDED PRACTICE for Examples 2 and 3 Graph the inequality in a coordinate plane. 10. 2 x – 6 y > 9

GUIDED PRACTICE for Examples 4 and 5 Graph the inequality in a coordinate plane. 12. y< x– 2 +1 ANSWER

GUIDED PRACTICE for Examples 4 and 5 Graph the inequality in a coordinate plane. 13. y>– x+3 – 2 ANSWER

GUIDED PRACTICE for Examples 4 and 5 Graph the inequality in a coordinate plane. 14. y<3 x– 1 – 3 ANSWER

ESSENTIAL QUESTION What does a dashed boundary line on the graph of an inequality represent? The points on that line are not solutions of the inequality.