Chapter 2 Lesson 4 Objective To connect reasoning

Chapter 2 Lesson 4 Objective: To connect reasoning in algebra to geometry.

Properties of Equality • Addition Property If a=b, then a+c = b+c • Subtraction Property If a=b, then a-c = b-c • Multiplication Property If a=b, then a • c = b • c • Division Property If a=b and c≠ 0, then a/c = b/c • Reflexive Property a=a • Symmetric Property If a=b, then b=a • Transitive Property If a=b and b=c, then a=c • Substitution Property If a=b, then b can replace a in any expression

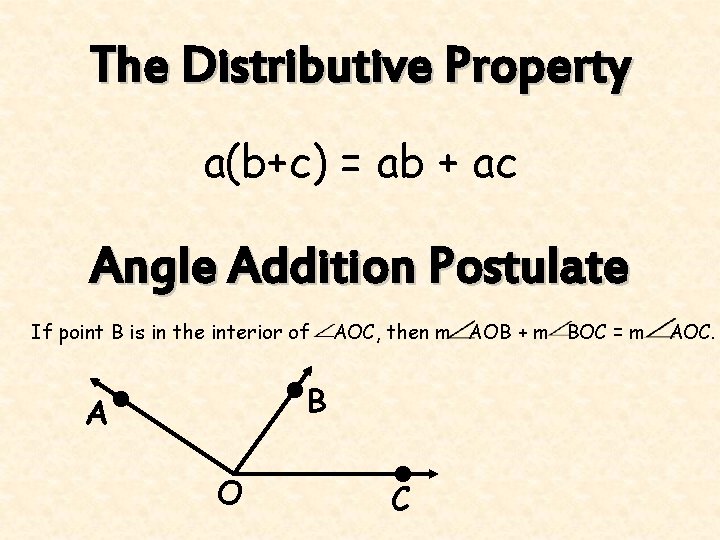
The Distributive Property a(b+c) = ab + ac Angle Addition Postulate If point B is in the interior of A AOC, then m AOB + m BOC = m • B • O • C AOC.

Example 1: • A • Solve for x and justify each step. Given: m m AOC = 139 AOB + m BOC = m x + 2 x + 10 = 139 3 x = 129 x = 43 B x° O • C (2 x + 10)° AOC Angle Addition Postulate Substitution Property Simplify Subtraction Property of = Division Property of =

Example 2: Justify each step used to solve 5 x – 12 = 32 + x for x. 5 x = 44 + x 4 x = 44 X = 11 Addition Property of Equality Subtraction Property of Equality Division Property of Equality

Example 3: M • K • Fill in each missing reason. (2 x+ 40 )° L LM bisects m MLN = m KLN KLM 4 x° Given Definition of angle bisector 4 x = 2 x + 40 Substitution Prop. ___________ 2 x = 40 Subtraction Prop. of Equality ___________ x = 20 Division Prop. Of Equality ___________ • N

Example 4: Solve for y and justify each step. Given: AC = 21 2 y A 3 y-9 B AB + BC = AC Segment Addition Postulate 2 y + (3 y – 9) = 21 Substitution Property 5 y – 9 = 21 Simplify 5 y = 30 Addition Property of Equality Y=6 Division Property of Equality C

Properties of Congruence Reflexive Property AB AB A Symmetric Property If AB If A Transitive Property A CD, then CD AB B, then B A If AB CD and CD EF, then AB EF If A B and B C, then A C.

Example 5: Name the property of equality or congruence that justifies each statement. a. K K Reflexive Property of Congruence b. If 2 x – 8 = 10, then 2 x = 18 Addition Property of Equality c. If x = y and y + 4 = 3 x, then x + 4 = 3 x. Substitution Property of Equality d. If RS TW and TW PQ, then RS PQ. Transitive Property of Congruence

Homework Page 91 -93 #1 -30