Chapter 2 Lasso for linear models Statistics for

Chapter 2: Lasso for linear models Statistics for High-Dimensional Data (Buhlmann & van de Geer)

Lasso � Proposed by Tibshirani (1996) � Least Absolute Shrinkage and Selection Operator � Why we still use it � Accurate in prediction and variable selection (under certain assumptions) and computationally feasible

2. 2. Introduction and preliminaries � Univariate response Yi � Covariate vector Xi � Can be fixed or random variables � Typically independence assumed, but Lasso can be applied to correlated data � For simplicity, we can assume the intercept is zero and all covariates are centered and measured on the same scale � Standardization

2. 2. 1. The Lasso estimator � “Shrunken” least squares estimator � βj=0 for some j � Convex optimization – computationally efficient � Equivalent to solving: � For λ) � some R (data-dependent 1: 1 correspondence between R and Estimating the variance � Can use residual sum of squares and df of Lasso � Or we can estimate β and σ2 simultaneously (Ch. 9)

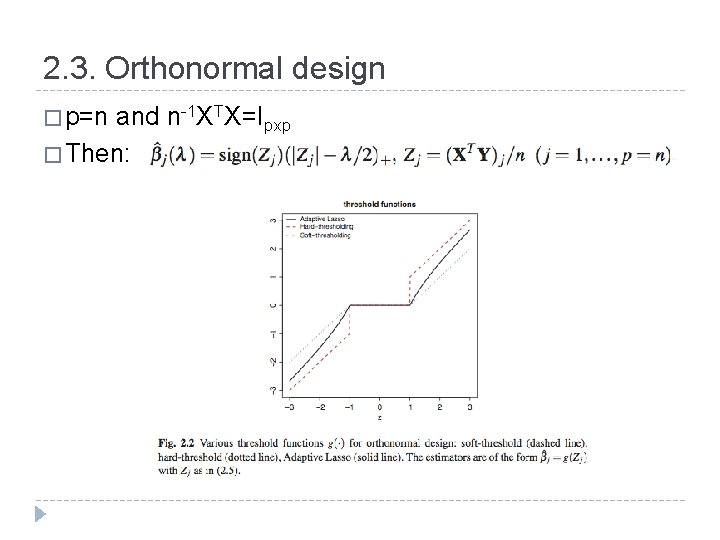
2. 3. Orthonormal design � p=n and n-1 XTX=Ipxp � Then:

2. 4. Prediction � Often cross-validation used to choose the λ minimizing the squared-error risk � Cross-validation can also be used to assess the predictive accuracy � Some asymptotics (more in Ch. 6) � For high-dimensional scenarios (allowing p to depend on n) � For consistency, we assume sparsity � Then:

2. 5. Variable screening � Under certain assumptions including (true) model sparsity and conditions on the design matrix (Thm. 7. 1), for a suitable range of λ, � � We For q=1, 2; derivation in Ch. 6 can use the Lasso estimate as variable screening: Variables with non-zero coefficients remain the same across different solutions (>1 solution for non-convex optimization such as when p>n) � The number of variables estimated as non-zero doesn’t exceed min(n, p) � And �

Lemma 2. 1. and tuning parameter selection � � Tuning � For parameter selection prediction, smaller λ is preferred, while larger penalty is needed for good variable selection (discussed more in Ch. 10 -11) � The smaller λ tuned from CV can be utilized for the screening process

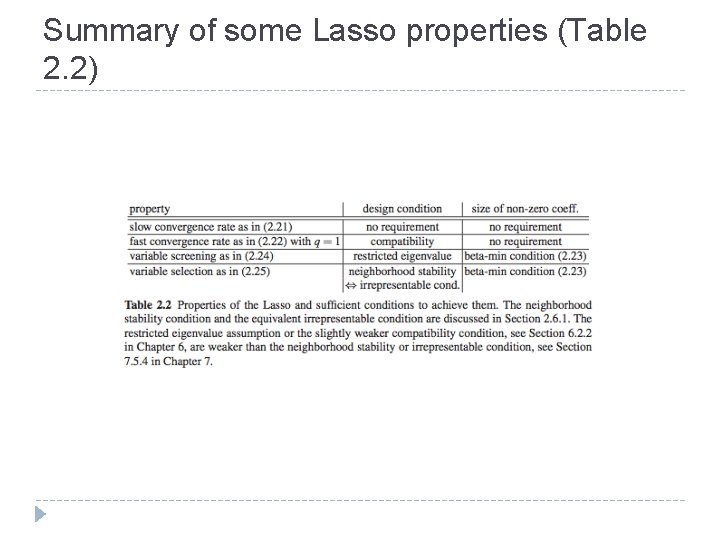
2. 6. Variable selection � AIC � and BIC use the l 0 -norm as a penalty Computation is infeasible for any relatively large p, since the objective function using this norm is non-convex � For � The set of all Lasso sub-models denoted by: � Then and � We want to know whether is contained in and if so, which value of λ will identify S 0 � With a “neighborhood stability” assumption on X (more later) and assuming � Then for

2. 6. 1. Neighborhood stability and irrepresentable condition � In order for consistency of Lasso’s variable selection, we make assumptions about X � WLOG, let the first s 0 variables form the active set S 0 � Let � Then the irrepresentable condition is: � Above is sufficient condition for consistency of Lasso model selection; RHS is “<=1” for necessary condition � This is easier to represent than the neighborhood stability condition but the two are equivalent for � Essentially consistency fails under too much linear dependence within sub-matrices of X

Summary of some Lasso properties (Table 2. 2)

2. 8. Adaptive Lasso � Two-stage procedure instead of just using l 1 -penalty: � Lasso can be used for the initial estimation, with CV for λ tuning, followed by the same procedure for the second stage � The adaptive Lasso gives a small penalty to βj with initial estimates of large magnitude

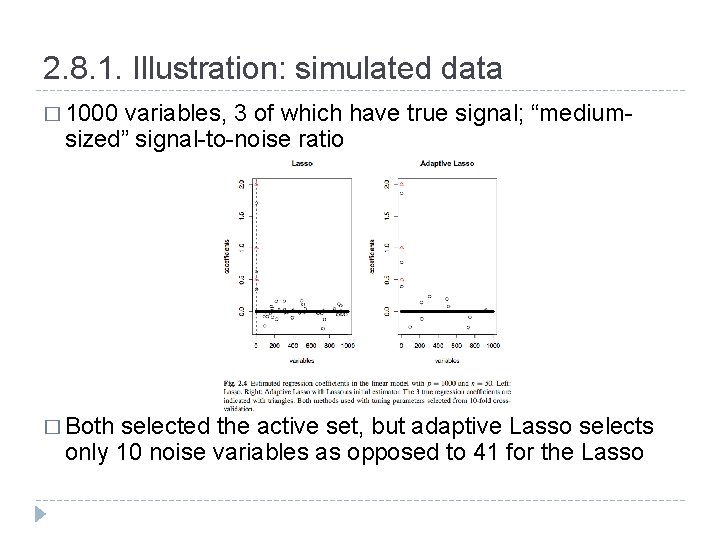
2. 8. 1. Illustration: simulated data � 1000 variables, 3 of which have true signal; “mediumsized” signal-to-noise ratio � Both selected the active set, but adaptive Lasso selects only 10 noise variables as opposed to 41 for the Lasso

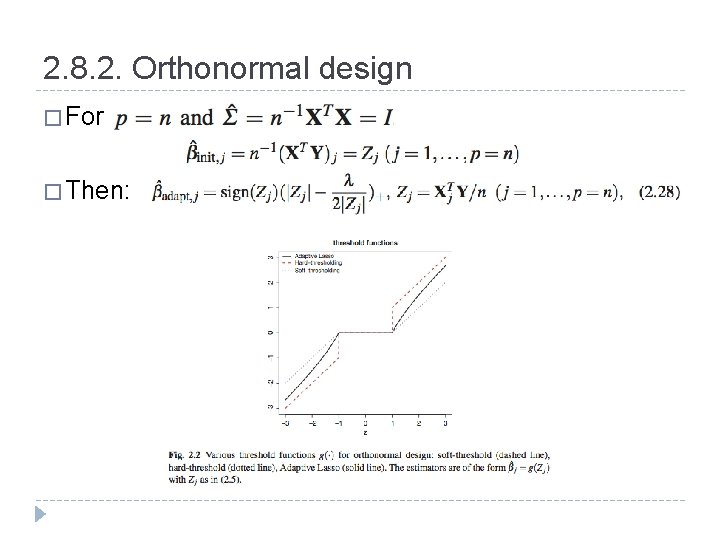
2. 8. 2. Orthonormal design � For � Then:

2. 8. 3. The adaptive Lasso: variable selection under weak conditions � For consistency of variable selection of the adaptive Lasso, we need large enough non-zero coefficients: � But we can assume weaker conditions than the neighborhood stability (irrepresentable) condition on the design matrix required for consistency of the Lasso (more in Ch. 7) � Then:

2. 8. 4. Computation � We can reparameterize into a Lasso problem: � Then � If the objective function is: a solution to this is Lasso is given by: � Any , then the solution for the adaptive algorithm for computing Lasso estimates can be used to compute the adaptive Lasso (more on algorithms later)

2. 8. 5. Multi-step adaptive Lasso � Procedure as follows:

2. 8. 6. Non-convex penalty functions � General � Ex: � penalized linear regression: SCAD (Smoothly Clipped Absolute Deviation) Non-differentiable at zero and non-convex � SCAD is related to the multi-step weighted Lasso: � Another non-convex penalty function commonly used is the lr-norm for r close to zero (Ch. 6 -7)

2. 9. Thresholding the Lasso � If we want a sparser model, instead of the adaptive Lasso we can threshold the Lasso estimates: � Then we can refit the model (via OLS) for the non-zero estimates: � Theoretical properties are as good as or better than the adaptive Lasso (more in Ch. 6 -7) � The tuning parameters can be chosen sequentially as in the adaptive Lasso

2. 10. The relaxed Lasso � First stage: all possible sub-models (across λ) � Second stage: computed � With smaller penalty to lessen the bias of Lasso estimation � Performs similarly to adaptive Lasso in practice � ϕ=0 yields the Lasso-OLS hybrid model � Lasso first stage, OLS second stage

2. 11. Degrees of freedom of the Lasso � We denote the hat operator by which maps the observed values to the fitted values � Then from Stein’s theory on unbiased risk estimation, � For MLEs, df=# of parameters � For linear hat operators (such as OLS) � For low-dimensional case with rank(X)=p, � This yields the estimator � Then the BIC can be used to to select λ:

2. 12. Path-following algorithms � We typically want to compute the estimator for many values of λ � We can compute the entire regularized solution path over all λ � Because the solution path is piecewise linear in λ: Typically the number of cutpoints λk are O(n). � The modified LARS algorithm (Efron 2004) can be used to construct the whole regularized solution path � � Exact method

2. 1. Coordinatewise optimization and shooting algorithms � For very high-dimensional problems coordinate descent algorithms are much faster than exact methods such as the LARS algorithm � With loss functions other than squared error loss, exact methods are often not possible � It is often sufficient to compute estimates over a grid of λ values : � With such that

Optimization (continued) � Let � The and update in step 4 is explicit due to squared-error loss function:

2. 13. Elastic net: an extension � Double-penalization � After version of Lasso: correction: � This is equivalent to the Lasso under orthonormal design