CHAPTER 2 Here are some ideas that might

CHAPTER 2

Here are some ideas that might help you with the summer HW … This is a brief overview. . . Please “watch” this in slide show mode … That means either DOWNLOAD this and open as a slide show … or open as a google slide AND watch in VIEW/PRESENT mode

PART 1: Vocabulary Terms PART 2: Word problems

PART 1: Vocabulary Terms

To DESCRIBE motion • Position • Time Go ahead and watch the following youtube video • Then come back to this power point Discussed by Neil Degrasse Tyson https: //www. youtube. com/watch? v=R 1 cexcjdy IE

To DESCRIBE motion ■ We need to know … ■ How far ■ In Which DIRECTION ■ Fast or Slow ■ Is speed CHANGING? (Same speed/ Speeds up/ Slows down)

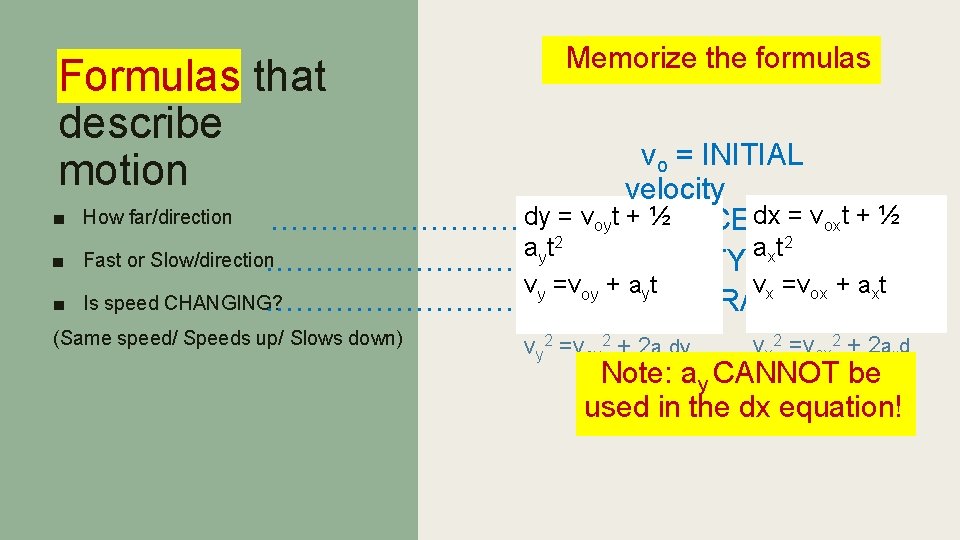
DESCRIBE the motion ■ How far & in Which …………… DIRECTION dy, s ■ Fast or Slow, in which …………… Direction ■ Is speed CHANGING? …………… (Same speed/ Speeds up/ Slows down) DISPLACEMENT d, dx, VELOCITY v ACCELERATION a

Formulas that describe motion ■ ■ ■ Memorize the formulas vo = INITIAL velocity How far/direction d ==vvotox+t + dx ½½ at 2 dy = voy. DISPLACEMENT t+½ …………… 2 2 a t y Fast or Slow/direction…………… VELOCITY v x=vo + at vx =vox + axt vy =voy + ayt Is speed CHANGING? …………… ACCELERATION v 2 =v 2 + 2 adx (Same speed/ Speeds up/ Slows down) o vy 2 =voy 2 + 2 aydy vx 2 =vox 2 + 2 axd Note: ay CANNOT be used in the dx equation!

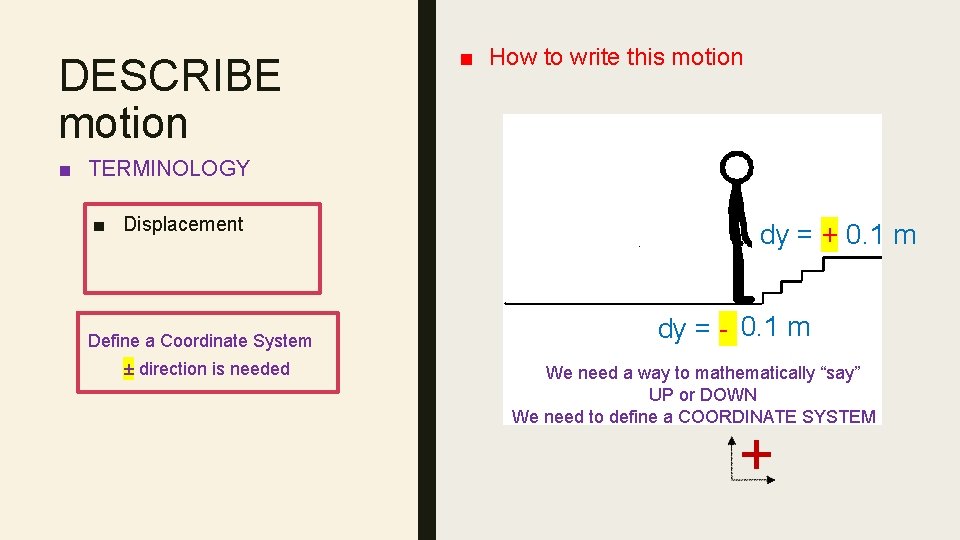
DESCRIBE motion ■ How to write this motion ■ TERMINOLOGY ■ Displacement Define a Coordinate System ± direction is needed dy =up + 0. 1 m down dy = - 0. 1 m We need a way to mathematically “say” UP or DOWN We need to define a COORDINATE SYSTEM +

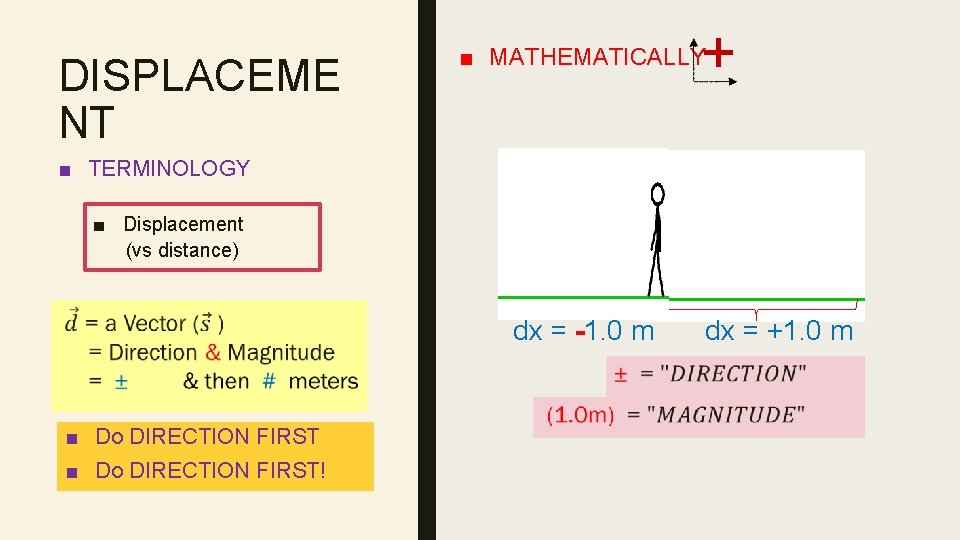
DISPLACEME NT + ■ MATHEMATICALLY ■ TERMINOLOGY ■ Displacement (vs distance) dx = -1. 0 m ■ Do DIRECTION FIRST! dx = +1. 0 m

DISPLACEME NT ■ TERMINOLOGY ■ Displacement (vs distance) ■ ■ MATHEMATICALLY But Who’s to say which way is +? YOU But with great power comes dx = -1. 0 m dx = +1. 0 m great responsibility …

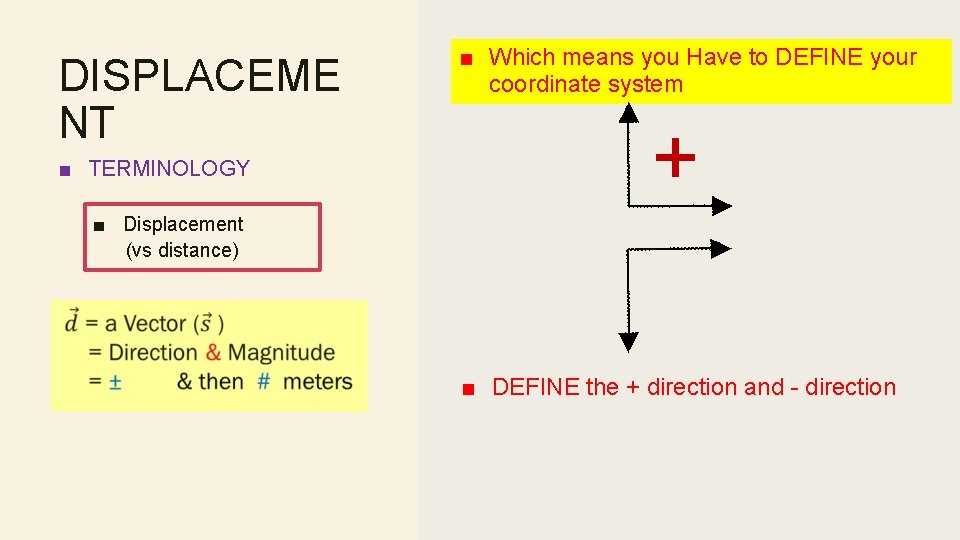
DISPLACEME NT ■ TERMINOLOGY ■ Which means you Have to DEFINE your coordinate system + ■ Displacement (vs distance) ■ DEFINE the + direction and - direction

DISPLACEME NT ■ TERMINOLOGY ■ ■ ■ Left Right Up Down North, South, East, West + ■ MATHEMATICALLY ■ If you DEFINE your coordinate system as this ■ ■ ■ Left …. . neg# Right …. . pos# Up …. . pos# Down …. . neg# North, East …. . pos# South, West …. . neg#

DISPLACEME NT + ■ MATHEMATICALLY ■ DEFINE your coordinate system ■ TERMINOLOGY ■ Displacement is a VECTOR ■ Do DIRECTION 1 st ■ Then worry about the #

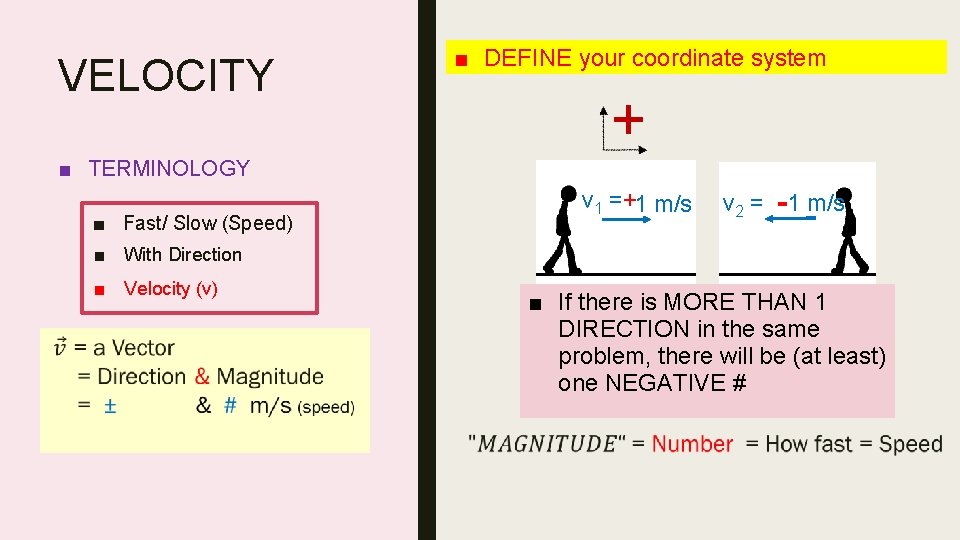
VELOCITY ■ TERMINOLOGY ■ Fast/ Slow (Speed) ■ DEFINE your coordinate system + v 1 =+1 m/s v 2 = -1 m/s ■ With Direction ■ Velocity (v) ■ If there is MORE THAN 1 DIRECTION in the same problem, there will be (at least) one NEGATIVE #

ACCELERATI ON ■ TERMINOLOGY ■ Same speed / Speed up/ Slow down ■ Change Direction? ■ Acceleration (a) a = change in velocity wrt time ■ MATHEMATICAL LY +

ACCELERATI ON ■ TERMINOLOGY ■ Same speed / Speed up/ Slow down ■ Direction ■ MATHEMATICAL LY + 1) Example: Both are CONSTANT SPEED (or 0 speed) ■ Acceleration (a) a = change in velocity wrt time a = 0 m/s 2 There is no change in speed or direction

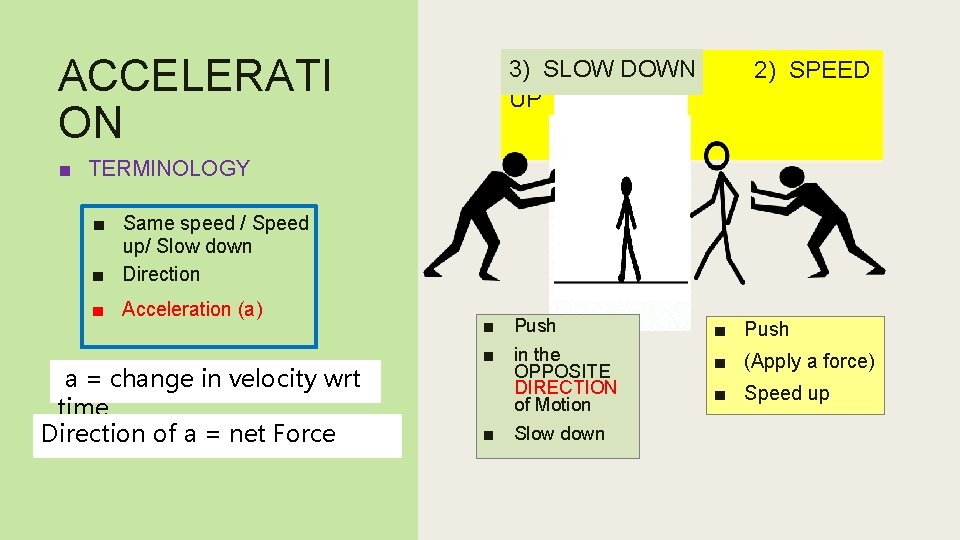
ACCELERATI ON 3) SLOW DOWN 2) SPEED How to make things change UP speed? ■ TERMINOLOGY ■ Same speed / Speed up/ Slow down ■ Direction ■ Acceleration (a) a = change in velocity wrt time Direction of a = net Force ■ Push ■ in the OPPOSITE DIRECTION of Motion ■ Slow down ■ Push ■ (Apply a force) ■ Speed up

■ How do we write it MATHEMATICALLY? ACCELERATI ■ 1 Write DIRECTION ON ■ DEFINE your coordinate system st ■ TERMINOLOGY + ■ Then write the # ■ Same speed / Speed up/ Slow down ■ Direction ■ Acceleration (a) a = change in velocity wrt time Direction of a = net Force a=+ ■ Push. DOWN SLOW in the a■= OPPOSITE of SIGNDirection as velocity Motion ■ Slow down! v=- a=- ■SPEED Push UP (Apply a. SIGN force) a■= SAME velocity ■ as Speed up

What if we choose our Coordinate System differently? +

■ DEFINE your coordinate system ACCELERATI ON ■ How do we tell MATHEMATICALLY? + ■ TERMINOLOGY ■ Same speed / Speed up/ Slow down ■ Direction ■ Acceleration (a) a = change in velocity wrt time v = + m/s a = - m/s 2 ■ Push. DOWN SLOW in the a■= OPPOSITE of SIGNDirection as velocity Motion ■ Slow down! a = +m/s 2 ■SPEED Push UP (Apply a. SIGN force) a■= SAME velocity ■ as Speed up

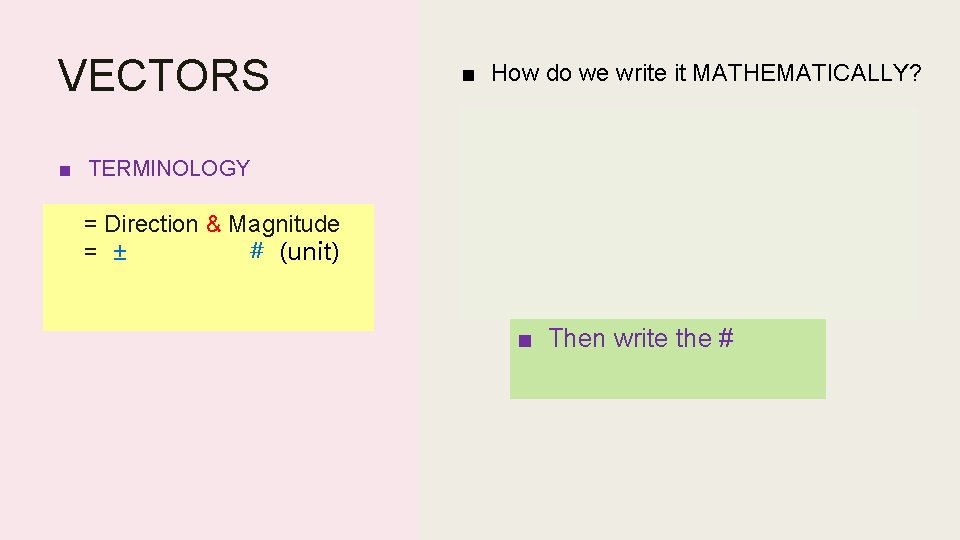
VECTORS ■ TERMINOLOGY = Direction & Magnitude = ± # (unit) ■ How do we write it MATHEMATICALLY? + ■ DEFINE your coordinate system ■ 1 st Write DIRECTION ■ Then write the #

PART 2: Word problems

For problems with scientific notation ■ Use the scientific notation BUTTON on your calculator ■ “EXP” ■ x 10 x ■ 2 nd “EE” (above the 7 button) Do not use the multiplication button, nor the ^ button, nor enter “ 10”

Here is an example to try ■ If an object travelling at constant speed covers 1. 92 x 1013 meters in a year (3. 2 x 107 seconds), what speed is it moving?

■ If an object travelling at constant speed covers 1. 92 x 1013 meters in a year (3. 2 x 107 seconds), what speed is it moving? FIRST: Enter “givens” into the a-v-d-t Table • Yes, it takes extra time • But it also slows one down enough to Ø catch mistakes and Ø allow insight

SOLUTION ■ If an object travelling at constant speed covers 1. 92 x 1013 meters in a year (3. 2 x 107 seconds), what speed is it moving? Hidden zeroes = one of the most important numbers in physics 0 ? 1. 92 x 1013 m 3. 2 x 107 s • And then put a “? ” for what we are solving for Ø Can’t tell you how many times students solve for the wrong thing

SOLUTION ■ If an object travelling at constant speed covers 1. 92 x 1013 meters in a year (3. 2 x 107 seconds), what speed is it moving? 2 nd comes the ALGEBRA (before #s) 0 ? 1. 92 x dx = vot + ½ at 2 1013 m 3. 2 x 107 s Write one of the given formulas Solve for unknown in terms of “given” symbols • • • Yes, it takes extra time But in the long run, this will REALLY help you And college board can take away points if you don’t do this step

SOLUTION ■ If an object travelling at constant speed covers 1. 88 x 1013 meters in a year (3. 2 x 107 seconds), what speed is it moving? 0 ? 1. 92 x 1013 m 3. 2 x 107 s Only after algebra, substitute in #s • College board gives a point for this step

SOLUTION ■ If an object travelling at constant speed covers 1. 88 x 1013 meters in a year (3. 2 x 107 seconds), what speed is it moving? 0 Time to plug into our calculator ? 1. 92 x 1013 m NOTE: NO parenthesis If you have a TI NO “ 10” NO ^ 3. 2 <2 nd EE> 7 enter: 1. 88 <2 nd EE> 13 3. 2 x 107 s = 5. 8750 x 105 (write 5 -8 digits from calculator) = 5. 9 x 105 m/s (2 sig figs because givens had 2) NOTE: This is the approximate speed our galaxy moves!!

That seemed like a lot for a little problem ■ You will get used to it - seriously ■ You will eventually even see the speed and power in it ■ Especially for complicated word problems ■ Summary: 1) Put givens into a-v-d-t table 2) Indicate your Find 3) Write formula or equation 4) Solve for unknown algebraically, in terms of “given” variables 5) Substitute/Write in #s 6) Plug into calculator …. Record 5 -8 digits … Then round to sig figs … include units

For each Word Problem v Especially VERTICAL problems ■ DEFINE your COORDINATE SYSTEM before doing anything else ■ Then write your GIVENS for a-v-d-t …. Write vectors with ± and then # ■ Write your “Find” ■ Remember the FORMULAS ■ Substitute the ± Given values into the algebraic solution ■ Solve on calculator … write down 5 -8 digits … then round with unit

For each Word Problem v Especially VERTICAL problems ■ COORDINATE SYSTEM ■ ± GIVENS ■ FORMULAS ■ SOLVE!

Example #2 ■ A ball is thrown down at 3. 0 m/s from 100. 0 m high. Where will it be after 2. 00 s?

■ A ball is thrown down at 3. 0 m/s from 100. 0 m high. Where will it be after 2. 00 s? ■ Define Whatyour is the NEW system first required coordinate step?

■ A ball is thrown down at 3. 0 m/s from 100. 0 m high. Where will it be after 2. 00 s? + ■ ■ ■ COORDINATE SYSTEM ■ ± GIVENS ■ FORMULAS ■ SOLVE! Because everything is DOWN, I will define DOWN as POSITIVE ± GIVENS FORMULAS a = +9. 8 m/s 2 dy = voyt + ½ ayt 2 vy =voy + ayt vy 2 =voy 2 + 2 aydy vo = +3. 0 m/s v= dy = ? t = 2. 00 s SOLVE dy = vot + ½ at 2 = (+3)(2) + ½(+9. 8)(2)2 = 25. 6 dy = 26 m DOWN from the TOP dy = (100 -26) = 74 m from the bottom (2 sf because the given 3. 0 had 2 sf)

Here is another example (#3) ■ A ball is thrown UP at 3. 0 m/s from 100. 0 m high. Where will it be after 2. 00 s?

Here is another example ■ A ball is thrown UP at 3. 0 m/s from 100. 0 m high. Where will it be after 2. 00 s? ■ Define Whatyour is the new first required coordinate system step?

■ A ball is thrown UP at 3. 0 m/s from 100. 0 m high. Where will it be after 2. 00 s? + ■ ■ ■ COORDINATE SYSTEM ■ ± GIVENS ■ FORMULAS ■ SOLVE! I can make UP POSITIVE because it starts upward ± GIVENS FORMULAS ay =-9. 8 m/s 2 dy = vot + ½ at 2 v =vo + at v 2 =vo 2 + 2 ad voy =+3. 0 m/s v= dy = ? t = 2. 00 s SOLVE dy = voyt + ½ ayt 2 = (+3)(2) + ½ (-9. 8)(2)2 = -13. 6 (neg means down) dy = 14 m DOWN from the TOP dy = (100 -13. 6) = 86 m from the bottom … 2 sf

■ A ball is thrown UP at 3. 0 m/s from 100. 0 m high. Where will it be after 2. 00 s? + ■ ■ ■ COORDINATE SYSTEM ■ ± GIVENS ■ FORMULAS ■ SOLVE! OR we keep DOWN as POSITIVE … but then voy will be a NEG # ± GIVENS FORMULAS a = +9. 8 m/s 2 dy = vot + ½ at 2 v =vo + at vo = -3. 0 m/s v= dy = ? t = 2. 00 s v 2 =vo 2 + 2 ad SOLVE dy = voyt + ½ ayt 2 = (-3)(2) + ½(+9. 8)(2)2 = -6 + 19. 6 = 13. 6 dy = 14 m DOWN from the TOP dy = (100 -14) = 86 m from the bottom … 2 sf

So there you have some word problem examples for Chapter 2 ■ Recommendations: 1) Remember to 1 st define coordinate system 2) Memorize formulas d = vot + ½ at 2 v =vo + at v 2 =vo 2 + 2 ad 3) Do NOT combine x-values into the same formula as yvalues 4) Remember to include ± signs for vectors 5) Solve algebraically first Note: You may be quizzed on these things

Chapter 2 also includes GRAPHING ■ To understand GRAPHING that is found in Chapter 2 ■ Watch the separate graphing power points

The end of this algebra section of Ch 2 - There are no questions to answer for this presentation