Chapter 2 Fourier Transform and Spectra Topics Spectrum

Chapter 2 Fourier Transform and Spectra Topics: Ø Spectrum by Convolution Ø Spectrum of a Switched Sinusoid Ø Power Spectral Density Ø Autocorrelation Huseyin Bilgekul & Erhan A. Ince Eeng 360 Communication Systems I Department of Electrical and Electronic Engineering Eastern Mediterranean University Eeng 360 1

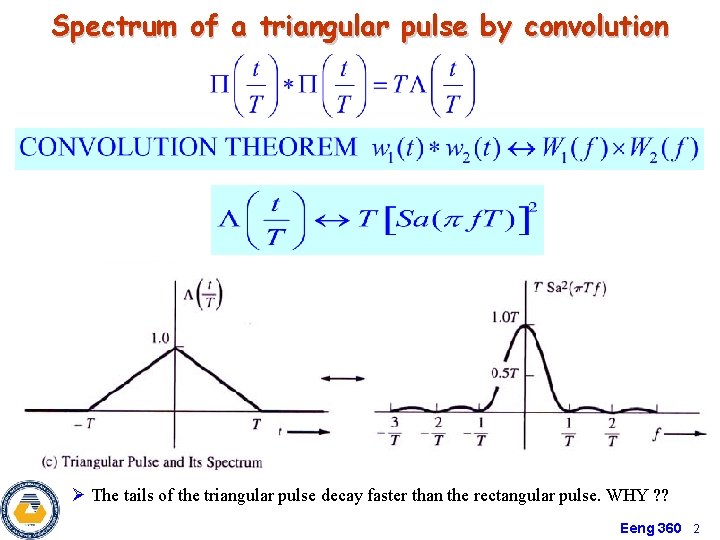
Spectrum of a triangular pulse by convolution Ø The tails of the triangular pulse decay faster than the rectangular pulse. WHY ? ? Eeng 360 2

Spectrum of a Switched Sinusoid Using the Frequency Translation Property of the Fourier Transform We can get a similar result using the convolution property of the Fourier Transform. Eeng 360 3

Spectrum of a Switched Sinusoid Eeng 360 4

Power Spectral Density (PSD) Ø We define the truncated version (Windowed) of the waveform by: • The average normalized power from the time domain: • Using Parseval’s theorem to calculate power from the frequency domain Eeng 360 5

Power Spectral Density Ø Definition: The Power Spectral Density (PSD) for a deterministic power waveform is • where w. T(t) ↔ WT(f) and Pw(f) has units of watts per hertz. • The PSD is always a real nonnegative function of frequency. • PSD is not sensitive to the phase spectrum of w(t) • The normalized average power is • This means the area under the PSD function is the normalized average power. Eeng 360 6

Eeng 360 7

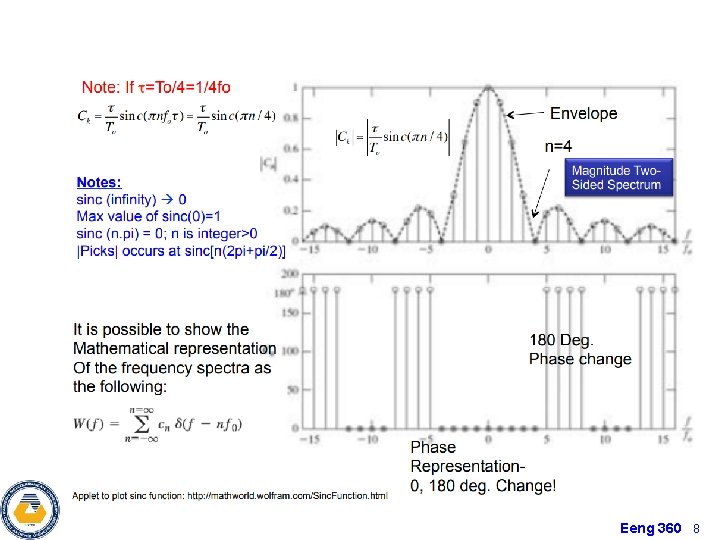
Eeng 360 8

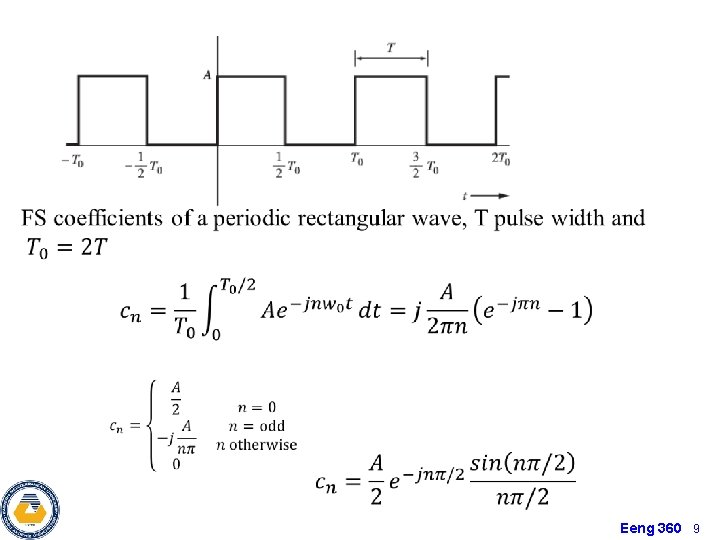
Eeng 360 9

Eeng 360 10

Normalized power for a periodic waveform where cn are the complex Fourier coefficients of the waveform Eeng 360 11

Eeng 360 12

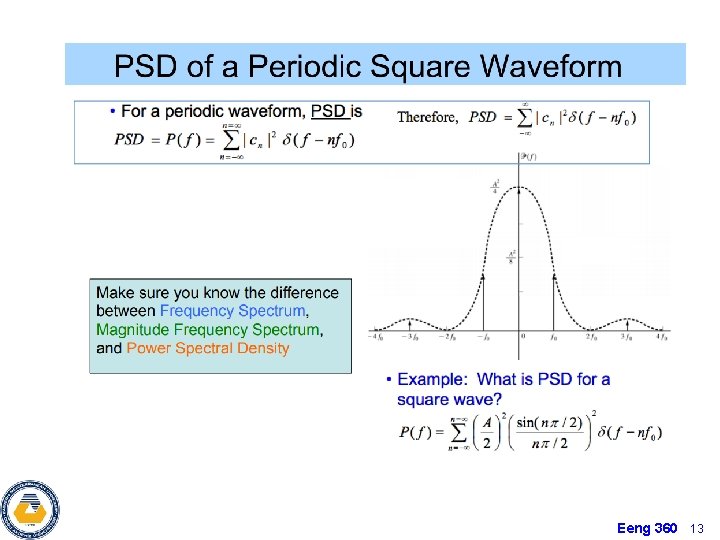
Eeng 360 13

Autocorrelation Function Ø Definition: The autocorrelation of a real (physical) waveform is • Wiener-Khintchine Theorem: PSD and the autocorrelation function are Fourier transform pairs; The PSD can be evaluated by either of the following two methods: 1. Direct method: by using the definition, 2. Indirect method: by first evaluating the autocorrelation function and then taking the Fourier transform: Pw(f)= ℑ [Rw(τ) ] • The average power can be obtained by any of the four techniques. Eeng 360 14

PSD of a Sinusoid Eeng 360 15

PSD of a Sinusoid Ø The average normalized power may be obtained by using: Eeng 360 16