Chapter 2 Fourier Transform and Spectra Topics Fourier













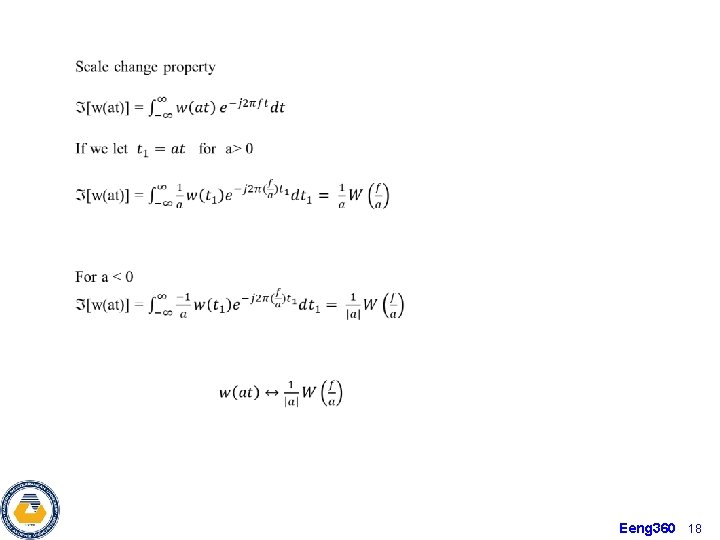













- Slides: 41

Chapter 2 Fourier Transform and Spectra Topics: Ø Fourier transform (FT) of a waveform Ø Properties of Fourier Transforms Ø Parseval’s Theorem and Energy Spectral Density Ø Dirac Delta Function and Unit Step Function Ø Rectangular and Triangular Pulses Ø Convolution Erhan A. Ince Eeng 360 Communication Systems I Department of Electrical and Electronic Engineering Eastern Mediterranean University Eeng 360 1

Fourier Transform of a Waveform Ø Definition: Fourier transform The Fourier Transform (FT) of a waveform w(t) is: where ℑ[. ] denotes the Fourier transform of [. ] f is the frequency parameter with units of Hz (1/s). Ø W(f) is also called two-sided spectrum of w(t), since both positive and negative frequency components are obtained from the definition Eeng 360 2

Evaluation Techniques for FT Integral Ø One of the following techniques can be used to evaluate a FT integral: • • Direct integration. Tables of Fourier transforms or Laplace transforms. FT theorems. Superposition to break the problem into two or more simple problems. • Differentiation or integration of w(t). • Numerical integration of the FT integral on the PC via MATLAB or Math. CAD integration functions. • Fast Fourier transform (FFT) on the PC via MATLAB or Math. CAD FFT functions. Eeng 360 3

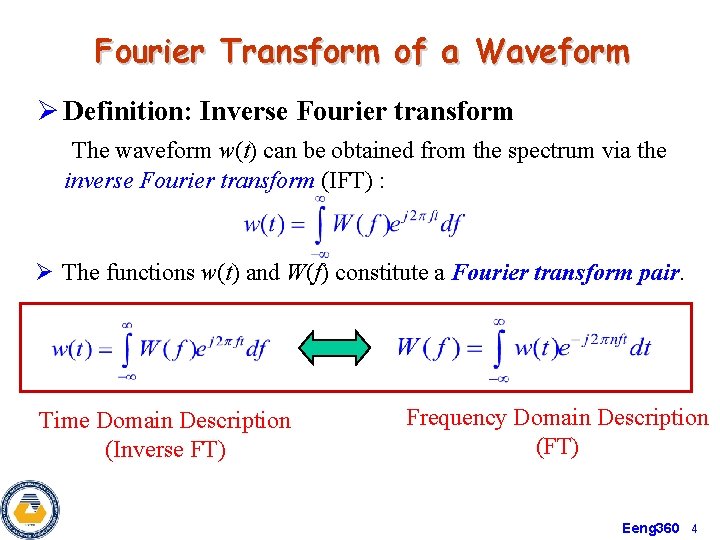
Fourier Transform of a Waveform Ø Definition: Inverse Fourier transform The waveform w(t) can be obtained from the spectrum via the inverse Fourier transform (IFT) : Ø The functions w(t) and W(f) constitute a Fourier transform pair. Time Domain Description (Inverse FT) Frequency Domain Description (FT) Eeng 360 4

Quadrature components Phasor components Eeng 360 5

Fourier Transform - Sufficient Conditions Ø • • The waveform w(t) is Fourier transformable if it satisfies the Dirichlet conditions: 1) Over any time interval of finite length, the function w(t) is single valued with a finite number of maxima and minima, and the number of discontinuities (if any) is finite. 2) w(t) is absolutely integrable. That is, Above conditions are sufficient, but not necessary. A weaker sufficient condition for the existence of the Fourier transform is: Finite Energy • • where E is the normalized energy. This is the finite-energy condition that is satisfied by all physically realizable waveforms. • Conclusion: All physical waveforms encountered in engineering practice are Fourier transformable. Eeng 360 6

Spectrum of an Exponential Pulse Eeng 360 7

Phasor components Eeng 360 8

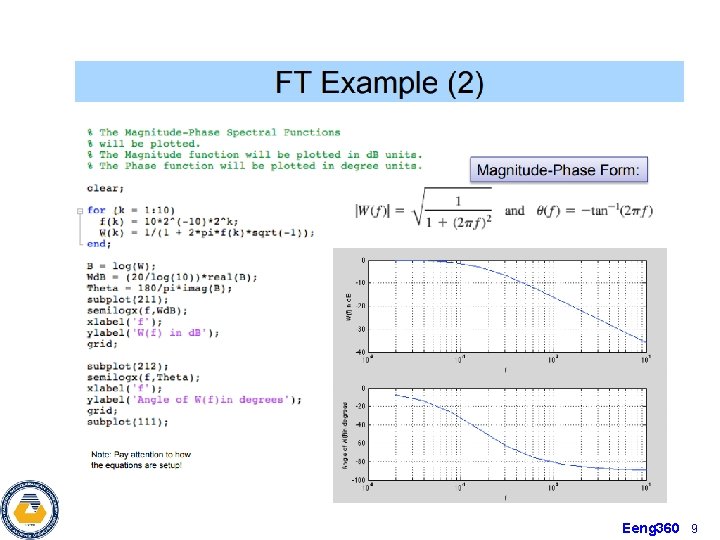
Eeng 360 9

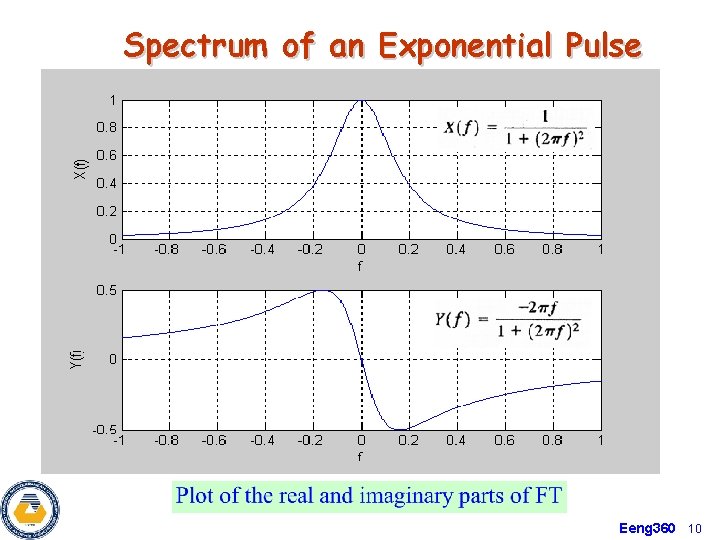
Spectrum of an Exponential Pulse Eeng 360 10

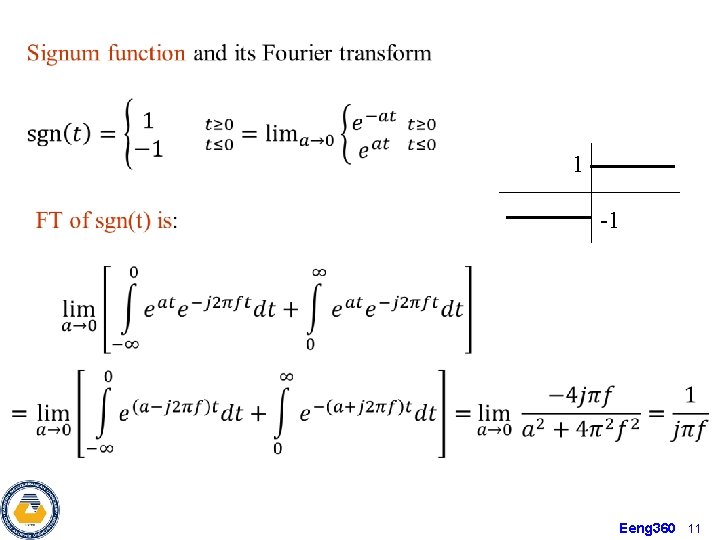
1 -1 Eeng 360 11

Eeng 360 12

Properties of Fourier Transforms Ø Theorem : Spectral symmetry of real signals If w(t) is real, then asterisk denotes conjugate operation. • Proof: Take the conjugate Substitute -f = Since w(t) is real, w*(t) = w(t), and it follows that W(-f) = W*(f). • If w(t) is real and is an even function of t, W(f) is real. • If w(t) is real and is an odd function of t, W(f) is imaginary. Eeng 360 13

Properties of Fourier Transforms Ø Spectral symmetry of real signals. If w(t) is real, then: • Magnitude spectrum is even about the origin. |W(-f)| = |W(f)| • (A) Phase spectrum is odd about the origin. θ(-f) = - θ(f) (B) Corollaries of Since, W(-f) = W*(f) We see that corollaries (A) and (B) are true. Eeng 360 14

Properties of Fourier Transform • f, called frequency and having units of hertz, is just a parameter of the FT that specifies what frequency we are interested in looking for in the waveform w(t). • The FT looks for the frequency f in the w(t) over all time, that is, over -∞ < t < ∞ • W(f ) can be complex, even though w(t) is real. • If w(t) is real, then W(-f) = W*(f). Eeng 360 15

Parseval’s Theorem and Energy Spectral Density Ø Persaval’s theorem gives an alternative method to evaluate energy in frequency domain instead of time domain. Ø In other words energy is conserved in both domains. (2 -41) Eeng 360 16

Parseval’s Theorem and Energy Spectral Density The total Normalized Energy E is given by the area under the Energy Spectral Density Eeng 360 17
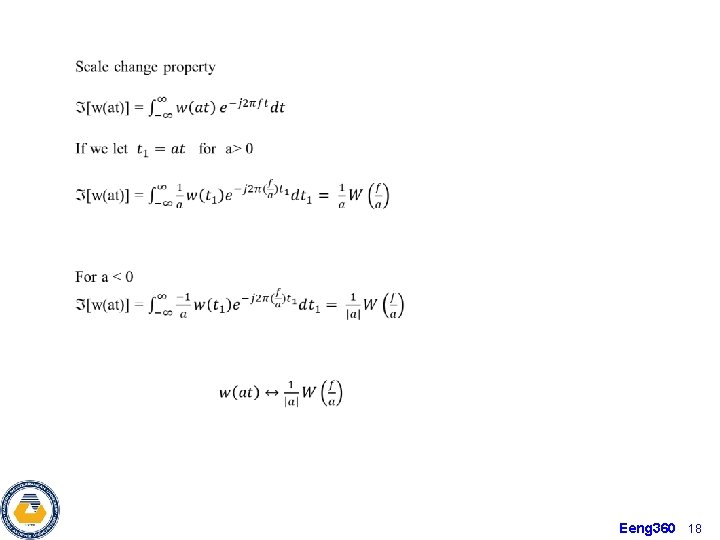
Eeng 360 18

TABIE 2 -1: Properties in Spectrum Domain Eeng 360 19

Example 2 -3: Spectrum of a Damped Sinusoid Eeng 360 20

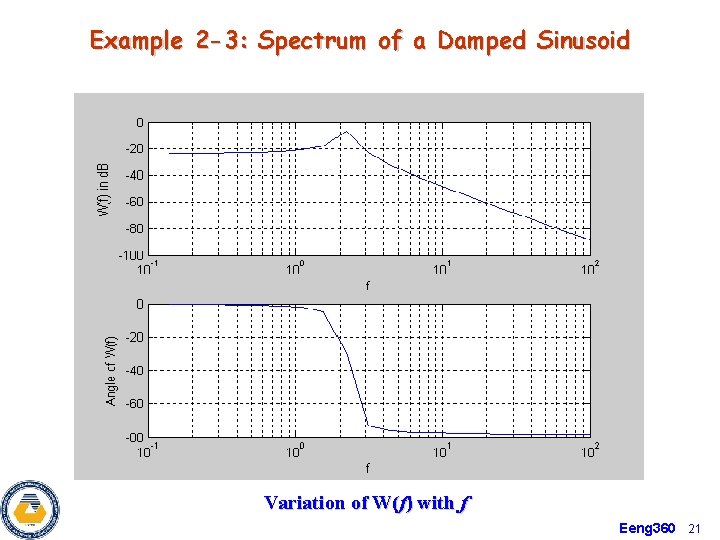
Example 2 -3: Spectrum of a Damped Sinusoid Variation of W(f) with f Eeng 360 21

Dirac Delta Function Ø Definition: The Dirac delta function δ(x) is defined by d(x) x where w(x) is any function that is continuous at x = 0. An alternative definition of δ(x) is: The Sifting Property of the δ function is If δ(x) is an even function the integral of the δ function is given by: Eeng 360 22

Unit Step Function Ø Definition: The Unit Step function u(t) is: Because δ(λ) is zero, except at λ = 0, the Dirac delta function is related to the unit step function by Eeng 360 23

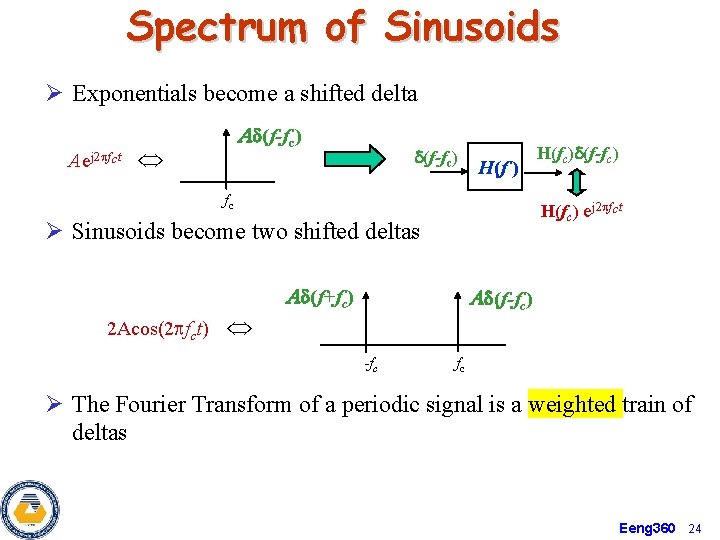
Spectrum of Sinusoids Ø Exponentials become a shifted delta Aej 2 pfct Ad(f-fc) H(f ) fc H(fc) ej 2 pfct Ø Sinusoids become two shifted deltas 2 Acos(2 pfct) H(fc)d(f-fc) Ad(f+fc) Ad(f-fc) -fc fc Ø The Fourier Transform of a periodic signal is a weighted train of deltas Eeng 360 24

Spectrum of a Sine Wave + Eeng 360 25

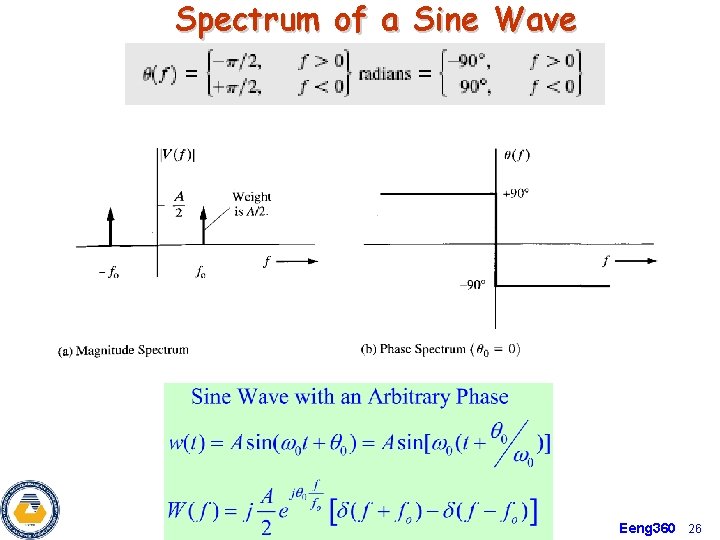
Spectrum of a Sine Wave Eeng 360 26

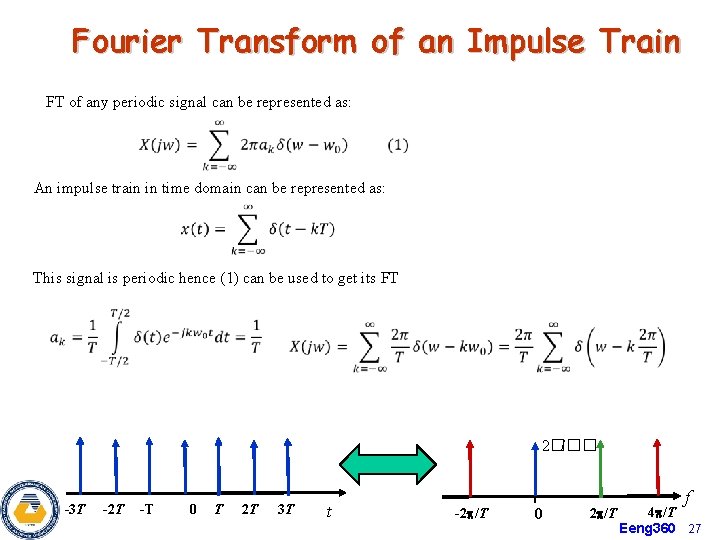
Fourier Transform of an Impulse Train FT of any periodic signal can be represented as: An impulse train in time domain can be represented as: This signal is periodic hence (1) can be used to get its FT 2�� /�� -3 T -2 T -T 0 T 2 T 3 T t -2 /T 0 2 /T f 4 /T Eeng 360 27

Eeng 360 28

Eeng 360 29

Eeng 360 30

Eeng 360 31

Eeng 360 32

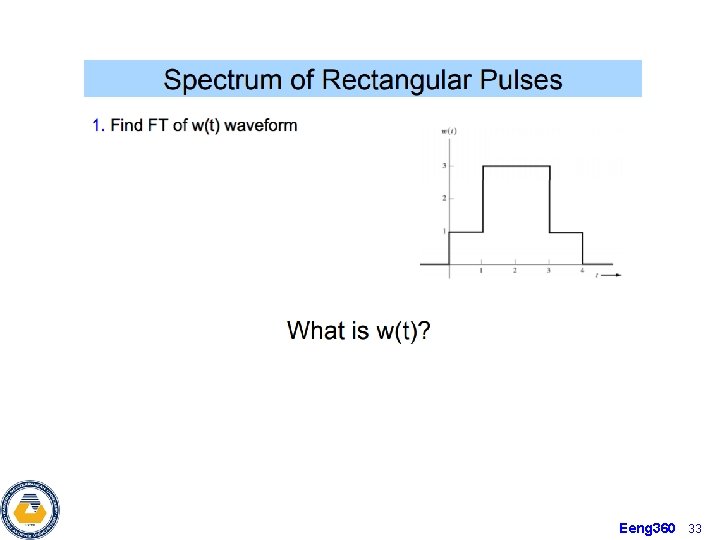
Eeng 360 33

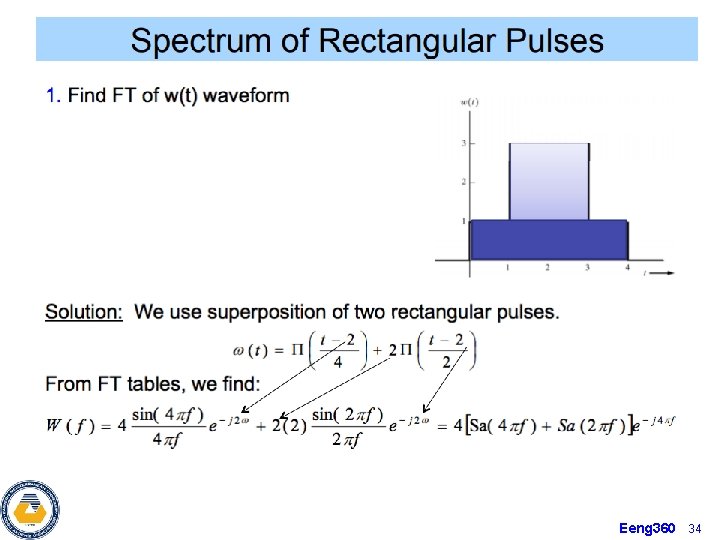
Eeng 360 34

https: //web. sonoma. edu/users/f/farahman/sonoma/courses/es 442/ Eeng 360 35

https: //web. sonoma. edu/users/f/farahman/sonoma/courses/es 442/ Eeng 360 36

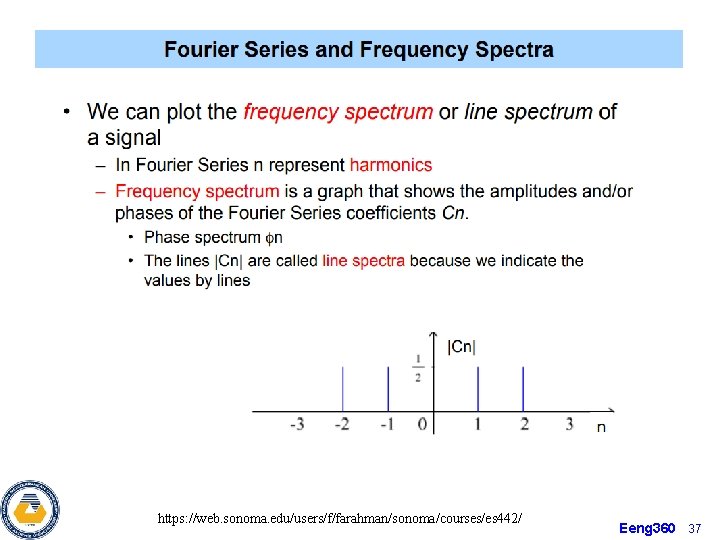
https: //web. sonoma. edu/users/f/farahman/sonoma/courses/es 442/ Eeng 360 37

https: //web. sonoma. edu/users/f/farahman/sonoma/courses/es 442/ Eeng 360 38

https: //web. sonoma. edu/users/f/farahman/sonoma/courses/es 442/ Eeng 360 39

https: //web. sonoma. edu/users/f/farahman/sonoma/courses/es 442/ Eeng 360 40

Eeng 360 41