CHAPTER 2 FORCE VECTORS 2 1 Scalars and

CHAPTER 2 FORCE VECTORS

2. 1 Scalars and Vector 1. Scalar A quantity characterized by a positive or negative number. EX: symbol Length Volume Mass L V M 2. Vector A quantity having both a magnitude and a direction. EX: position, force, moment line of action Symbol: or A magnitude: A= direction: degree c. c. w sense: arrowhead

2. 2 Vector operation 1. Scalar Multiplication and Division 2. Vector Addition Parallelogram Law

3. Vector Subtraction 4. Resolution of Vector (1) Known (2) Two line of action are known.

2. 3 Vector Addition of Force 1. Engineering problems (a) Find the resultant force, knowing its components. resultant force (b) Resolve a known force into two components. = ? ?

2. Analysis method a> Parallelogram law b> Trigonometry i> sine law ii> cosine law

2. 4 Addition of a System of Coplanar Forces 1. Rectangular components 2. Notation (1) scalar notation Algebraic scalars are used to express the magnitude and directional sense of the rectangular components of a force.

(2) Cartesian Vector Notation Cartesian unit vector i and j are used to express the directions of x and y axes respectively. The magnitude of each component of force F is always a positive quantity.

(1) Resolve each force into it x and y components using Cartesian vector notation.

(2) Add the respective components using scalar algebra (3) Form the resultant force by adding the resultant of the x and y components using the parallelogram law. magnitude orientation

2. 5 Cartesian Vectors 1. Right-Hand Coordinates system 2. Rectangular components of a vector

3. Unit vector A vector having a magnitude of 1. : a vector, unit vector of =? ? Unit vector (dimensionless) 4. Cartesian unit vectors i , j , k. Cartesian unit vector i , j , k are used to designate the direction of the x, y, z axes respectively.

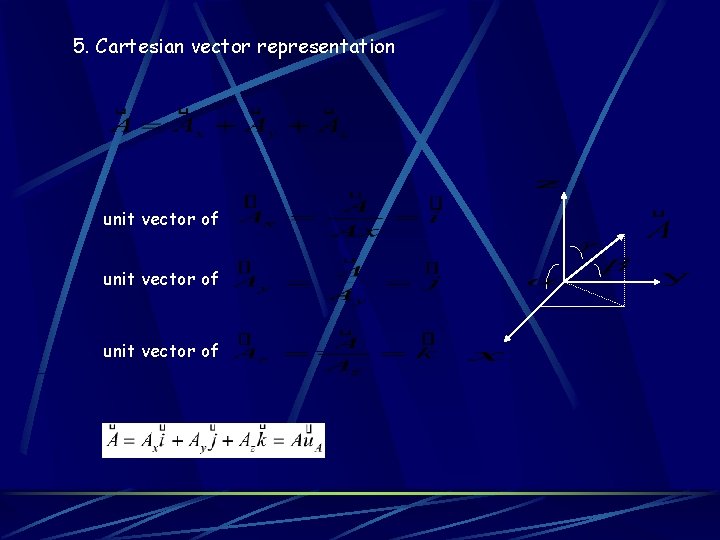
5. Cartesian vector representation unit vector of

(1) Magnitude of Cartesian vector A (2) Direction of Cartesian vector A The orientation of A is defined by the coordinate direction angles α β γ Direction consines cosα=Ax/A cosβ=Ay/A cosγ=Az/A Direction of A is defined by its unit of vector u. A

2 -6 Operations of cartesian vectors • Additon: A+B A=Axi+Ayj+Azk B=Bxi+Byj+Bzk R=A+B=(Ax+Bx)i+(Ay+By)j+ (Az+Bz)k 2. Subtraction A-B R`=A-B=(Ax-By)i+(Ax-By)j+ (Az-Bz)k 3. Concurrent Force System are algebraic sums of the respective x, y, z components of each force in the system.

2 -7 Position Vectors 1. Definition A position vector is a fixed vector which locates a point in space relative to another point. 2. Position vector from origin 0 to point P(x, y, z) Cartesian vector form of r 3. Position vector from point A to point B

2 -8 Force Vector Directed Along A Line u: Unit vector defines the direction and sense of position vector r and force vector F.

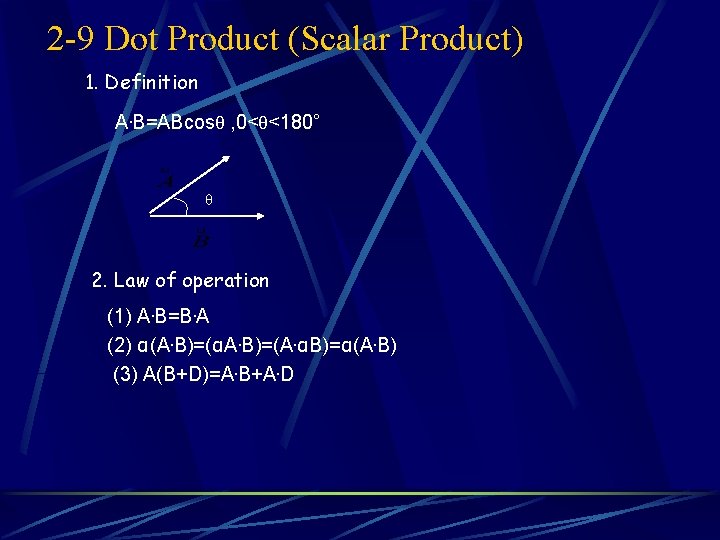
2 -9 Dot Product (Scalar Product) 1. Definition A. B=ABcosθ , 0<θ<180° θ 2. Law of operation (1) A. B=B. A (2) α(A. B)=(αA. B)=(A. αB)=α(A. B) (3) A(B+D)=A. B+A. D

3. Cartesian vector formulation (1) Dot product of Cartesian unit vector i. i=1*1*cos 0。=1 j. j=1 , k. k=1 i. j=1*1 cos 90。=0 , i. k=k. j=0 (2) Dot product of vectors A&B in Cartesian vector form A=Axi+Ayj+Ajk B=Bxi+Byi+Bjk A. B=(Axi+Ayj+Ajk). (Bxi+Byi+Bjk) =Ax. Bx+Ay. By+Az. Bz

4. Applications (1) Angle between two vectors θ (2) Components of a vector parallel and perpendicular to a line. A A: known vector θ: angle b/w A and u. u: unit vector of a line (known) θ