Chapter 2 Fluid Static Hydrostatic Forces and Buoyancy

Chapter 2 : Fluid Static/ Hydrostatic Forces and Buoyancy (P. 448) • Objective: ü Explain the hydrostatic forces applied on submerged plane surface. ü Hydrostatic forced on submerged curved surface. ü Define and explain Buoyancy and Stability. • Course Outcome: ü Ability to explain and analyze the fundamental principles of fluid mechanics ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 1

FLUID STATICS (P. 448) • • • Deals with problems associated with fluid at rest. No relative motion between adjacent layers. Thus, no shear stress (tangential stress) to deform the fluid. Liquid – hydrostatic; Gas – aerostatic. The only stress in fluid statics is normal stress (perpendicular to surface) • Normal stress is due to pressure (Pressure: gravity field-weight of fluid) • Variation of pressure is due only to the weight of the fluid → fluid statics is only relevant in presence of gravity fields. ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 2

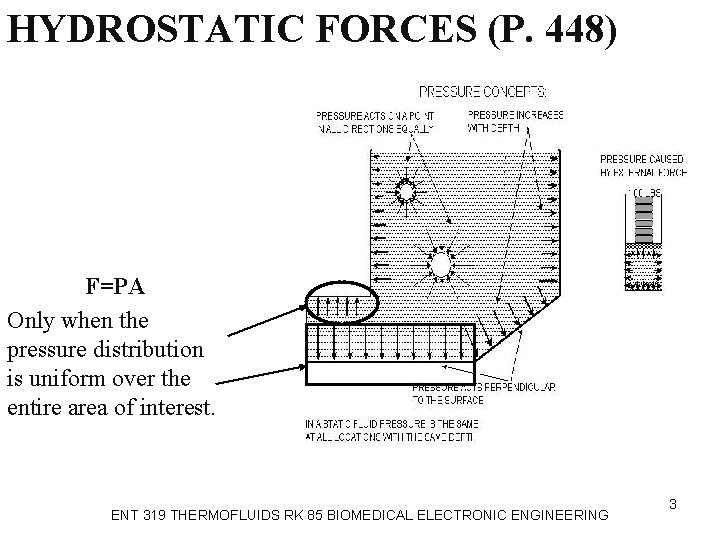
HYDROSTATIC FORCES (P. 448) F=PA Only when the pressure distribution is uniform over the entire area of interest. ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 3

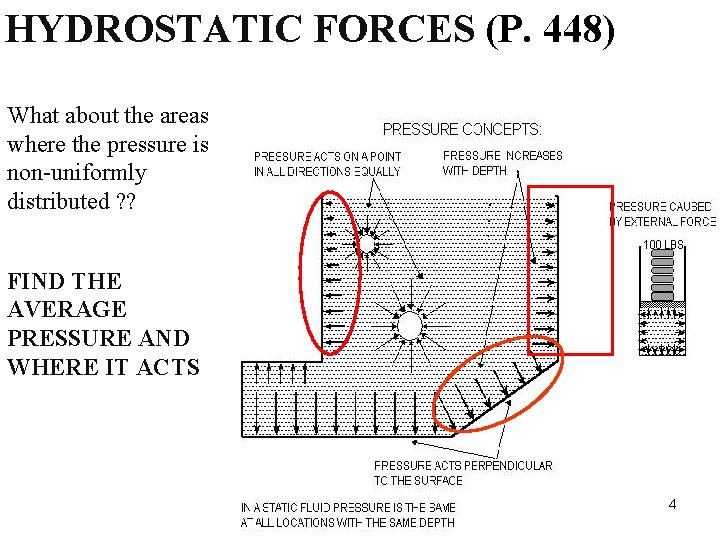
HYDROSTATIC FORCES (P. 448) What about the areas where the pressure is non-uniformly distributed ? ? FIND THE AVERAGE PRESSURE AND WHERE IT ACTS 4

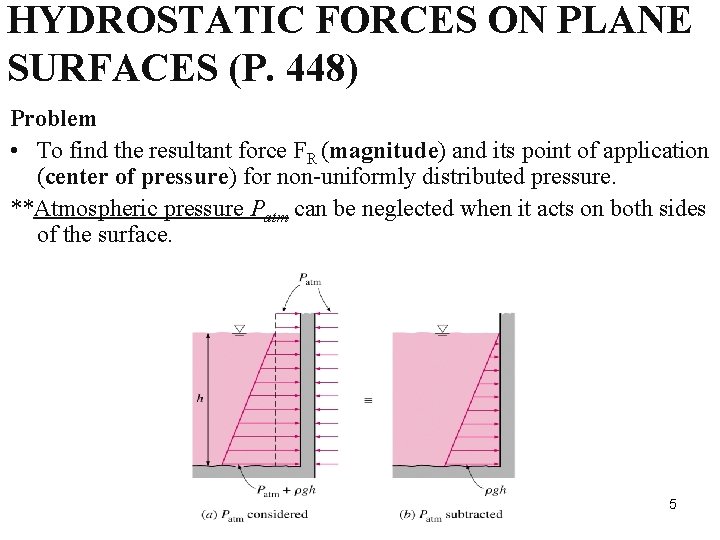
HYDROSTATIC FORCES ON PLANE SURFACES (P. 448) Problem • To find the resultant force FR (magnitude) and its point of application (center of pressure) for non-uniformly distributed pressure. **Atmospheric pressure Patm can be neglected when it acts on both sides of the surface. 5

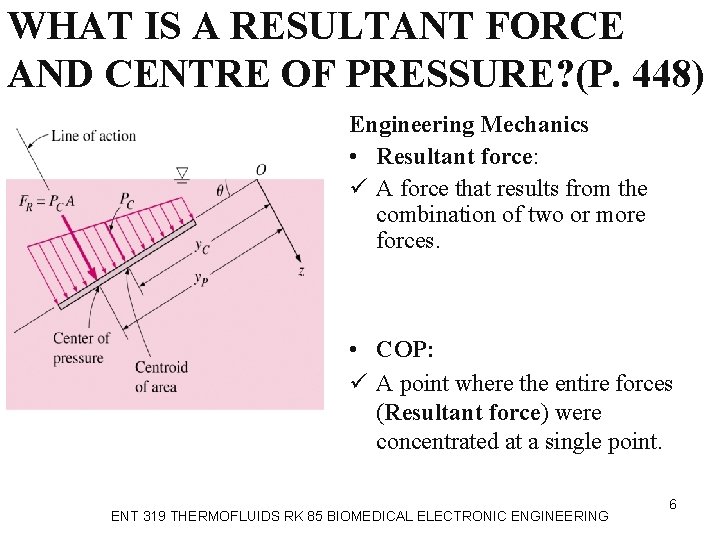
WHAT IS A RESULTANT FORCE AND CENTRE OF PRESSURE? (P. 448) Engineering Mechanics • Resultant force: ü A force that results from the combination of two or more forces. • COP: ü A point where the entire forces (Resultant force) were concentrated at a single point. ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 6

HOW TO DETERMINE THE RESULTANT FORCE, FR (P. 449) • Consider a flat plate completely submerged in a liquid. • Plane of the top surface intersects with horizontal surface with an angle Ө, the line of intersection will be the x axis. ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 7

HOW TO DETERMINE THE RESULTANT FORCE, FR (P. 449) Absolute pressure at any point of the fluid, P = Po + ρgh, h = y sin Ө = Po + ρgy sin Ө, FR = ∫Pd. A =∫ (Po + ρgy sin Ө)d. A = Po. A + ρg sin Ө ∫yd. A **∫yd. A is the first moment of area is related to the y coordinate of the centroid (or centre) of the surface by , yc= 1/A ∫yd. A. FR = (Po + ρgyc sin Ө) A = (Po + ρghc) A = P c. A The magnitude of the resultant force, FR acting on a plane surface of a completely submerged plate in a homogeneous (constant density) fluid is the product of the pressure, Pc, at the 8 centroid of the surface and the area A of the surface.

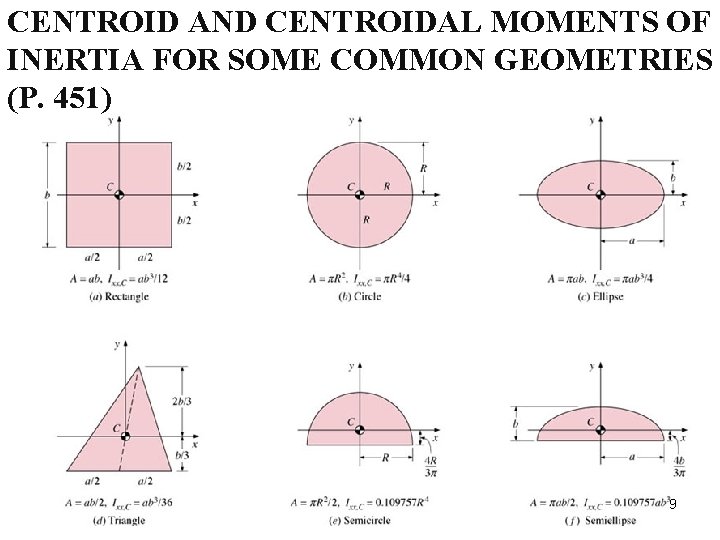
CENTROID AND CENTROIDAL MOMENTS OF INERTIA FOR SOME COMMON GEOMETRIES (P. 451) 9

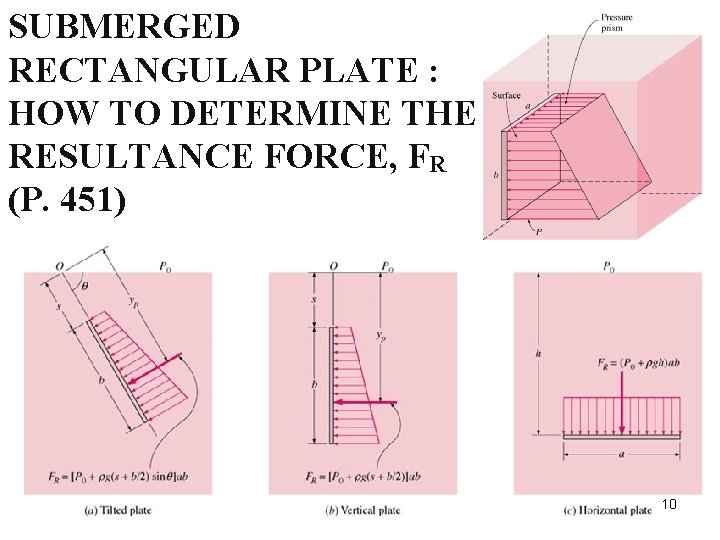
SUBMERGED RECTANGULAR PLATE : HOW TO DETERMINE THE RESULTANCE FORCE, FR (P. 451) 10

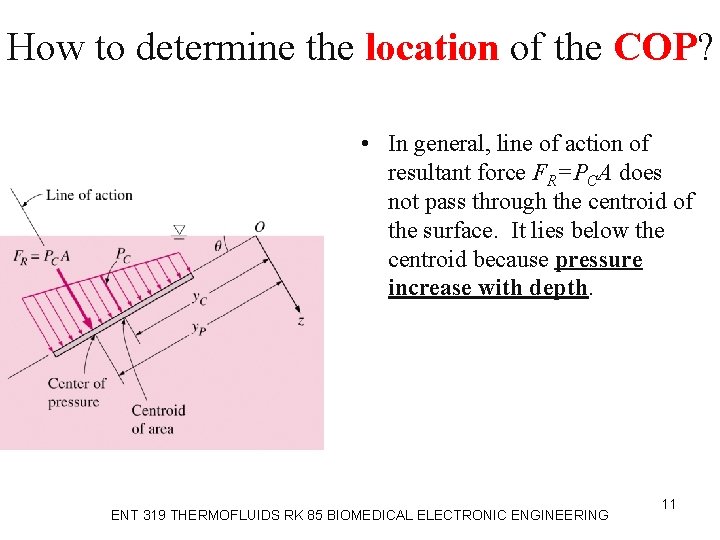
How to determine the location of the COP? • In general, line of action of resultant force FR=PCA does not pass through the centroid of the surface. It lies below the centroid because pressure increase with depth. ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 11

How to determine the location of the resultant force (Center of Pressure)? • The location of the line of action • The moment of the resultant force, FR = The moment of the distributed pressure force about the x-axis. • Then, ü yp. FR = ∫y. Pd. A =∫ y(Po + ρgy sin Ө)d. A = Po ∫ yd. A + ρgsin Ө ∫y 2 d. A = Poyc. A + ρgsin Ө Ixx, o : The second moment of area or the area moment of inertia ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 12

• Normally, the second moment of area is given about the axes passing through the centroid of the area. Therefore, we need parallel axis theorem to relate the Ixx, o and Ixx, c • Therefore, • If Po = 0 13

SUBMERGED RECTANGULAR PLATE : HOW TO DETERMINE THE C. O. P. 14

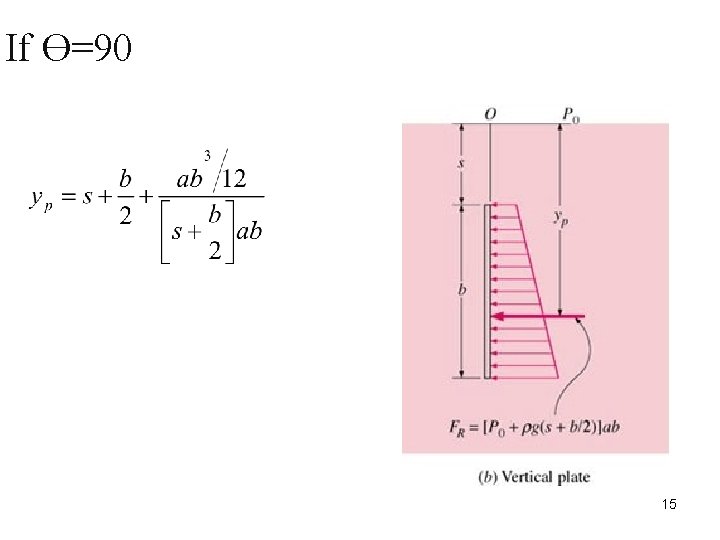
If Ө=90 15

• Example 1 ü Calculate FR, COP and discuss whether the driver can open the door or not. The moment acting on the mid point of the submerged door is 101. 3 k. N x 0. 5 m = 50. 6 k. Nm, which is 50 times of the moment the driver can possibly generate. CAN’T OPEN. 16

BUOYANCY (P. 451) Buoyant force: The upward force a fluid exerts on a body immersed in it. The buoyant force is caused by the increase of pressure with depth in a fluid. The buoyant force acting on the plate is equal to the weight of the liquid displaced by the plate. For a fluid with constant density, the buoyant force is independent of the distance of the body from the free surface. It is also independent of the density of the solid body. A flat plate of uniform thickness h submerged in a liquid parallel to the free surface. ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 17

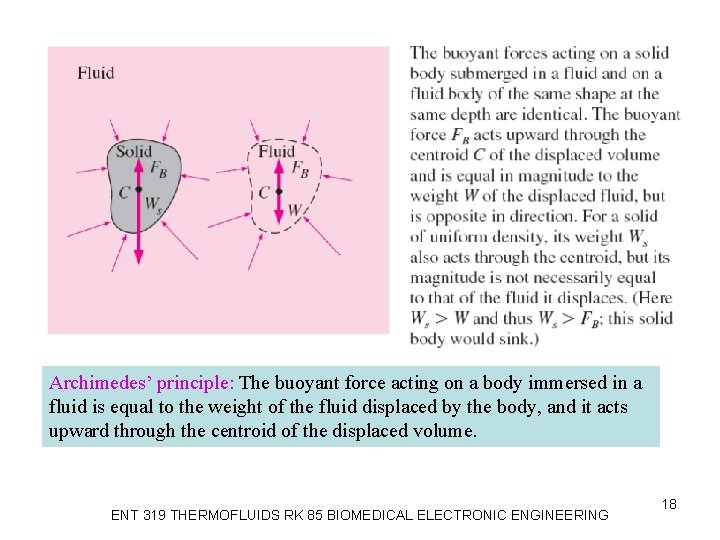
Archimedes’ principle: The buoyant force acting on a body immersed in a fluid is equal to the weight of the fluid displaced by the body, and it acts upward through the centroid of the displaced volume. ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 18

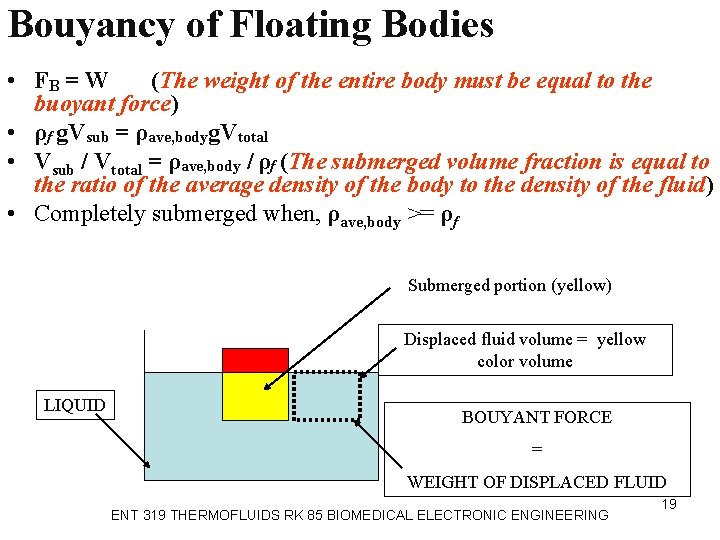
Bouyancy of Floating Bodies • FB = W (The weight of the entire body must be equal to the buoyant force) • ρf g. Vsub = ρave, bodyg. Vtotal • Vsub / Vtotal = ρave, body / ρf (The submerged volume fraction is equal to the ratio of the average density of the body to the density of the fluid) • Completely submerged when, ρave, body >= ρf Submerged portion (yellow) Displaced fluid volume = yellow color volume LIQUID BOUYANT FORCE = WEIGHT OF DISPLACED FLUID ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 19

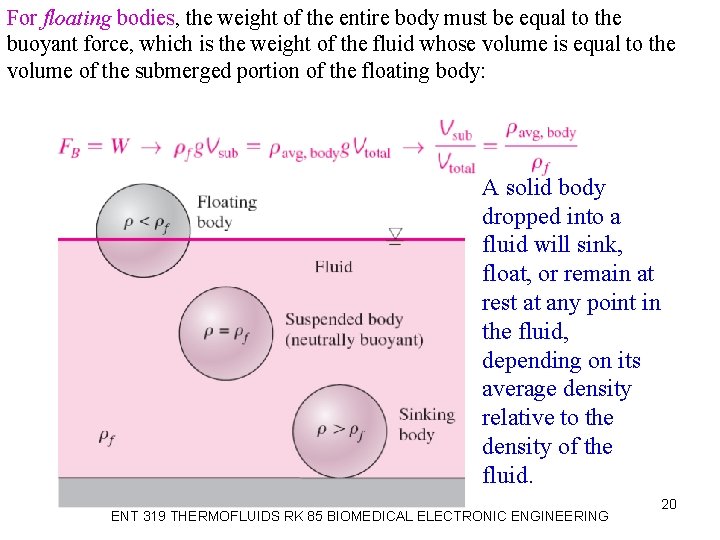
For floating bodies, the weight of the entire body must be equal to the buoyant force, which is the weight of the fluid whose volume is equal to the volume of the submerged portion of the floating body: A solid body dropped into a fluid will sink, float, or remain at rest at any point in the fluid, depending on its average density relative to the density of the fluid. ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 20

• The altitude of a hot air balloon is controlled by the temperature difference between the air inside and outside the balloon, since warm air is less dense than cold air. • When the balloon is neither rising nor falling, the upward buoyant force exactly balances the downward weight. ENT 319 THERMOFLUIDS RK 85 BIOMEDICAL ELECTRONIC ENGINEERING 21