Chapter 2 Errors in Numerical Methods and Their

Chapter 2 Errors in Numerical Methods and Their Impacts

Objectives • Know finite-word length effect • Know computing errors, their causes and impacts to numerical calculation • Know how to compute the errors • Know the effect of error propagation • Know how to avoid large errors

Content • Introduction • Finite word-length effect (Floating-point number representation) • Error • How to avoid error • Conclusion

Introduction • Why we need to know ? • Computers are great tools, however, without fundamental understanding of engineering problems, they will be useless.

Finite wordlength effect How floating numbers are stored in a computer ? Sign bit Exponent Mantissa Base of the number system used IEEE 64 -bit floating-point number representation

Finite wordlength effect

Finite wordlength effect Ex: 402 C 000000 S Exponent Mantissa 4 0 0 0 0 2 C 0 1 0 0 0 0 10 1 10 0 0 0 0 0 0 0 0 0 0 0 0 S=0 E = Exp-1023=1026 -1023=3 M = 1+0. 11 F = +(1. 11)2 x 23 = (1110)2=14 Check with MATLAB command: “hex 2 num”

Finite wordlength effect(cont’d) Step to convert from decimal number to IEEE stand. Check with MATLAB Use num 2 hex command S Exponent Mantissa 01000000000000000000000000000000 4 0 0 8 0 0 0

Finite wordlength effect(cont’d) How to add 2 numbers : This is done by bit alignment (only mantissa) with refer to the biggest number. Finally, the Mantissa words are added in 2’s system. Example : 1015 Ans: 1. 11000110101111110101001001101 x 21072 -1023 Example : 1 Ans: 1. 0 x 21023 -1023 Example : 1015+1 (show only Mantissa) Ans: 1015 110001101011111101010010011010000000000000000000000001000 Right shift 49 bits 1100011010111111010100100110100000001000 1

Finite wordlength effect(cont’d) 0 10000110000 1100011010111111010100100110100000001000 430 C 6 BF 526340008 How to substract 2 numbers : Complement and done by bit alignment with refer to the biggest number Example : 1015 -1 110001101011111101010010011010000000000000000000000001000 111111111111111111111111100011010111111010100100110011111111000 1015 2’s of 1

Finite wordlength effect(cont’d) 0 10000110000 1100011010111111010100100110011111111000 430 C 6 BF 52633 FFF 8 Will u try with the following problems? -1015 -1 -1015+1

Errors • • Error from numerical algorithm Truncation error Round-off error Overflow/Underflow Loss of significance Negligible addition Error magnification

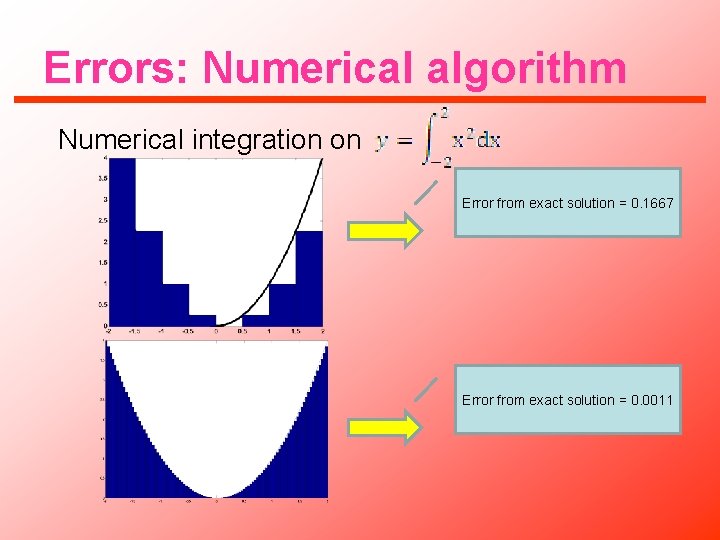
Errors: Numerical algorithm Numerical integration on Error from exact solution = 0. 1667 Error from exact solution = 0. 0011

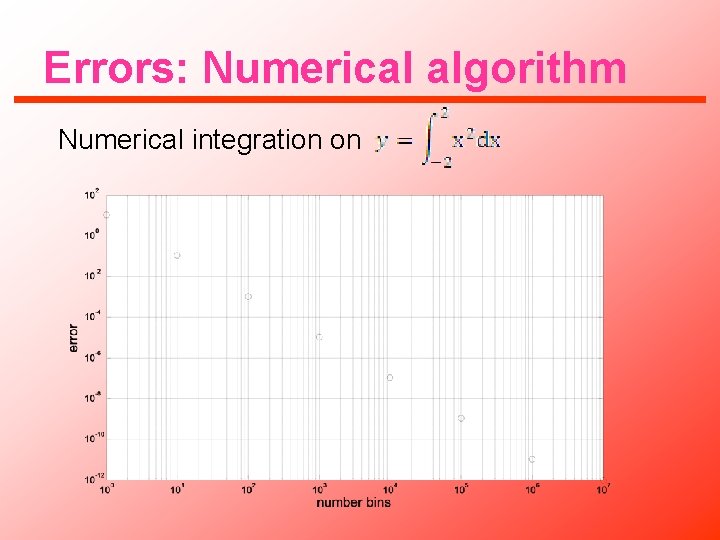
Errors: Numerical algorithm Numerical integration on

Errors: Truncation error is resulted from truncation series. Ex. Say x = 1 find exp(x)

Error: Loss of significance Bad subtraction in finite wordlength can create loss of significance. See the following example: Try with x= 1, 100, … 1015

Error: Propagation error Errors are propagated with the four arithmetic Operations. Let the exact values are X and Y, where their related values are x and y, respectively.

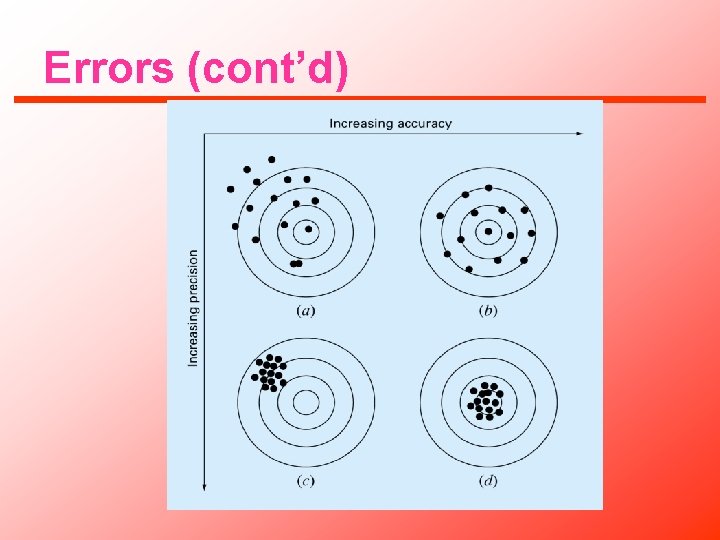
Errors • Accuracy. How close is a computed or measured value to the true value • Precision (or reproducibility). How close is a computed or measured value to previously computed or measured values. • Inaccuracy (or bias). A systematic deviation from the actual value. • Imprecision (or uncertainty or variance). Magnitude of scatter.

Errors (cont’d)

Errors (cont’d) Error Definitions True Value = Approximation + Error Et = True value – Approximation (+/-) True error MATLAB Example

Errors (cont’d) What u can see is we can’t estimate the true error for all cases !! (why ? ) So we use the following error definition instead. Approximation error …

Errors (cont’d) Apply approximation error to numerical approach (iterative) (+ / -) Define criteria : - Compute until Meaning that the result is correct at least n significant figures

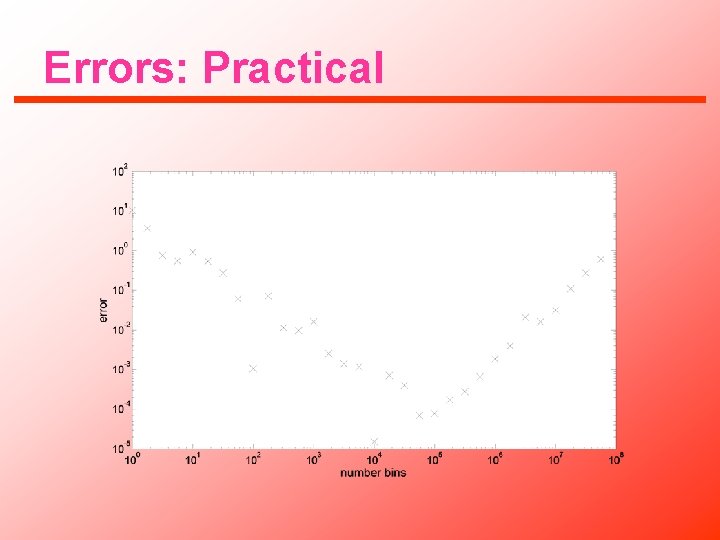
Errors: Practical