CHAPTER 2 EQUATION OF STATE An equation of

















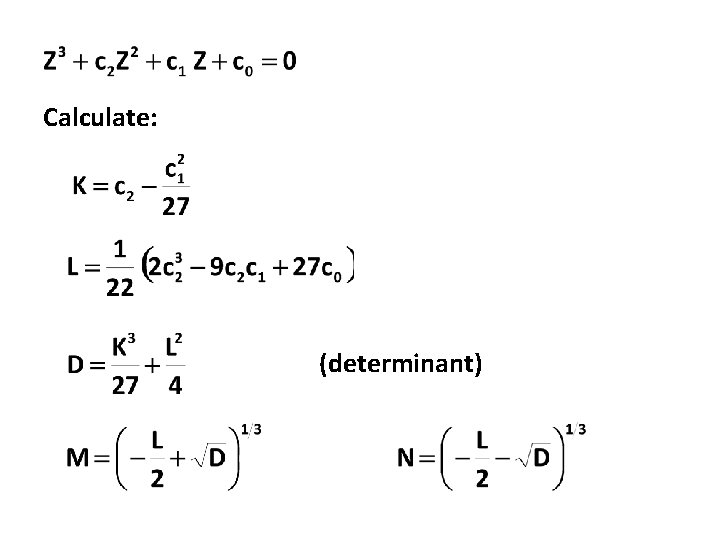
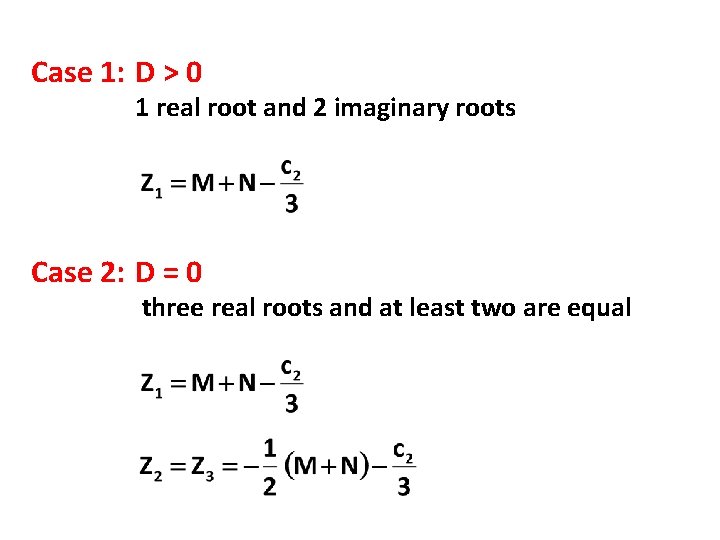


- Slides: 26

CHAPTER 2 EQUATION OF STATE

• An equation of state is a relation between state variables • It is a thermodynamic equation describing the state of matter under a given set of physical conditions. • It is a constitutive equation which provides a mathematical relationship between two or more state functions associated with the matter, such as its temperature, pressure, volume, or internal energy. • Equations of state are useful in describing the properties of fluids, mixtures of fluids, solids, and even the interior of stars.

CLASSICAL IDEAL GAS LAW PV = RT Assumption: 1) the gas consists of a large number of molecules, which are in random motion and obey Newton's laws of motion; 2) the volume of the molecules is negligibly small compared to the volume occupied by the gas; and 3) no forces act on the molecules except during elastic collisions of negligible duration.

CUBIC EQUATIONS OF STATE 1. Van der Waals equation of state 2. Redlich–Kwong equation of state 3. Soave modification of Redlich–Kwong 4. Peng–Robinson equation of state

VAN DER WAALS EQUATION OF STATE The van der Waals equation may be considered as the ideal gas law, “improved” due to two independent reasons: q Molecules are thought as particles with volume, not material points. Thus V cannot be too little, less than some constant. So we get (V – b) instead of V. q We consider molecules attracting others within a distance of several molecules' radii affects pressure we get dengan (P + a/V 2) instead of P.

where V is molar volume The substance-specific constants a and b can be calculated from the critical properties Pc, Tc, and Vc as

Cubic form of vd. W eos

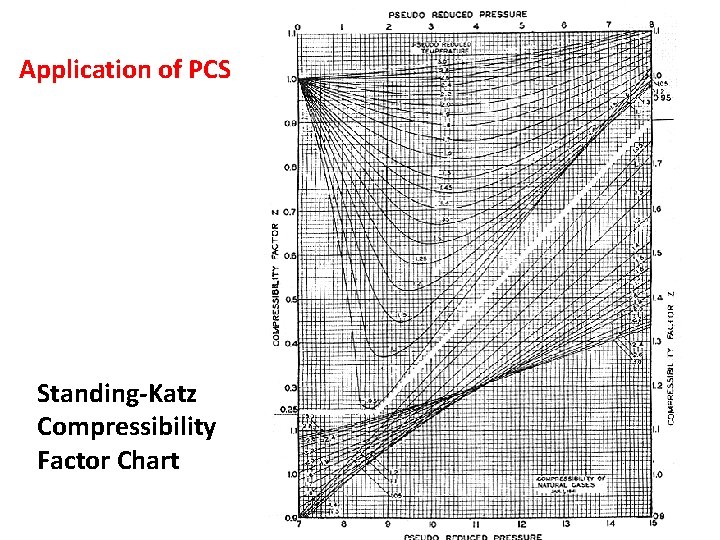
Principle of Corresponding States (PCS) The principle of Corresponding States (PCS) was stated by van der Waals and reads: “Substances behave alike at the same reduced states. Substances at same reduced states are at corresponding states. ” Reduced properties provide a measure of the “departure” of the conditions of the substance from its own critical conditions and are defined as follows

• The PCS says that all gases behave alike at the same reduced conditions. • That is, if two gases have the same “relative departure” from criticality (i. e. , they are at the same reduced conditions), the corresponding state principle demands that they behave alike. • In this case, the two conditions “correspond” to one another, and we are to expect those gases to have the same properties.

Reduced form of vd. W EOS: • This equation is “universal”. • It does not care about which fluids we are talking about. • Just give it the reduced conditions “Pr, Tr” and it will give you back Vr — regardless of the fluid. • As long as two gases are at corresponding states (same reduced conditions), it does not matter what components you are talking about, or what is the nature of the substances you are talking about; they will behave alike.

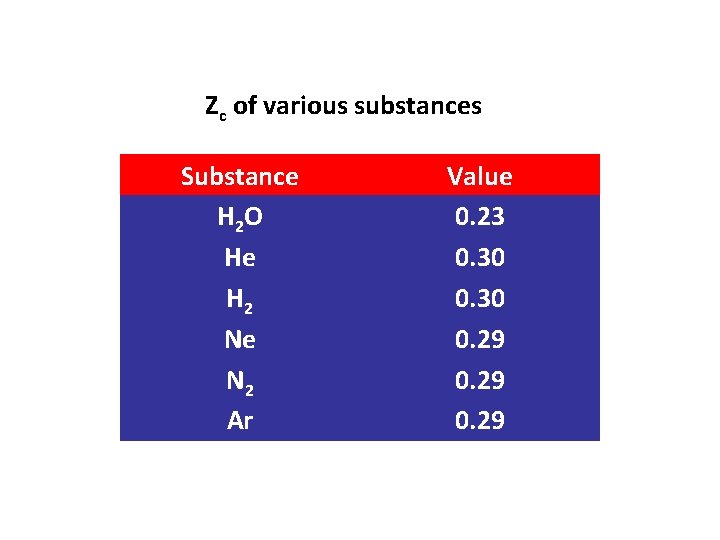
The compressibility factor at the critical point, which is defined as Zc is predicted to be a constant independent of substance by many equations of state; the Van der Waals equation e. g. predicts a value of 0. 375

Zc of various substances Substance H 2 O He H 2 Ne N 2 Ar Value 0. 23 0. 30 0. 29

Application of PCS Standing-Katz Compressibility Factor Chart

REDLICH-KWONG EOS The Redlich–Kwong equation is adequate for calculation of gas phase properties when:

Cubic form of RK eos

SOAVE-REDLICH-KWONG EOS

Cubic form of SRK eos

PENG-ROBINSON EOS

Cubic form of PR eos

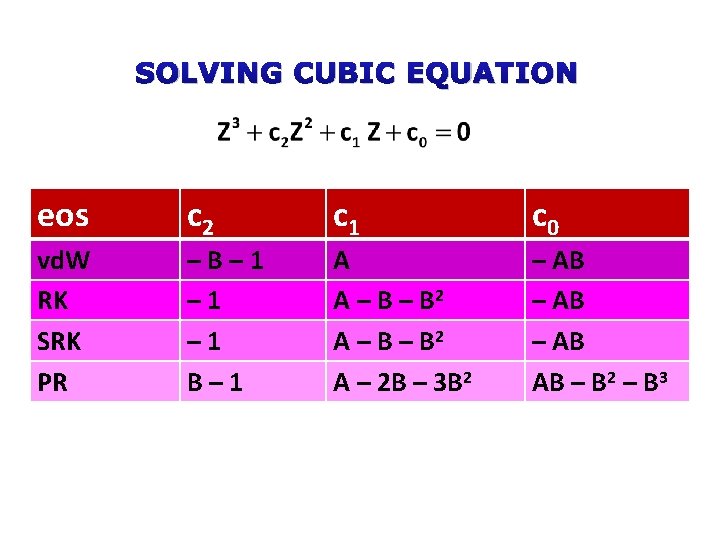
SOLVING CUBIC EQUATION eos c 2 c 1 c 0 vd. W RK SRK PR –B– 1 – 1 B– 1 A A – B – B 2 A – 2 B – 3 B 2 – AB AB – B 2 – B 3
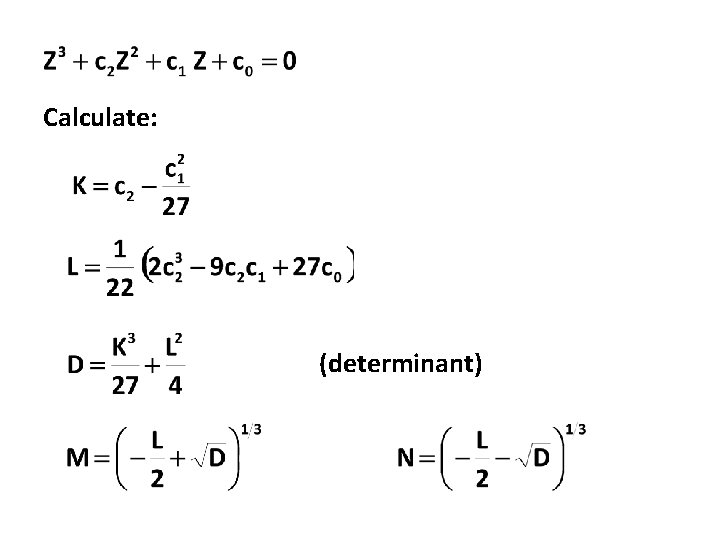
Calculate: (determinant)
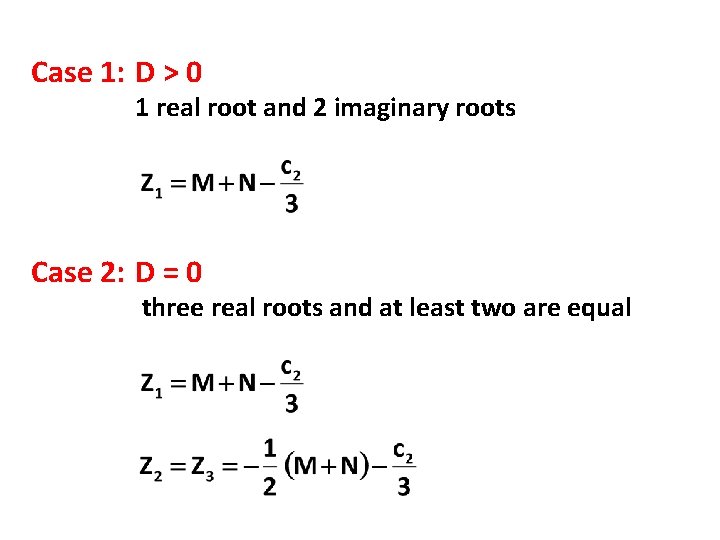
Case 1: D > 0 1 real root and 2 imaginary roots Case 2: D = 0 three real roots and at least two are equal

Case 3: D < 0 three, distinct, real roots Where k = 0 k=1 k=2 for for i=1 i=2 i=3 The minus sign applies when B > 0, The plus sign applies when B < 0.

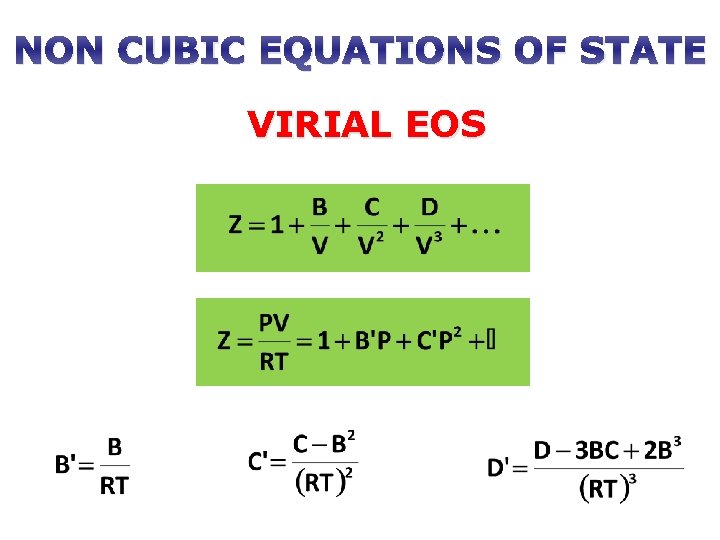
NON CUBIC EQUATIONS OF STATE VIRIAL EOS

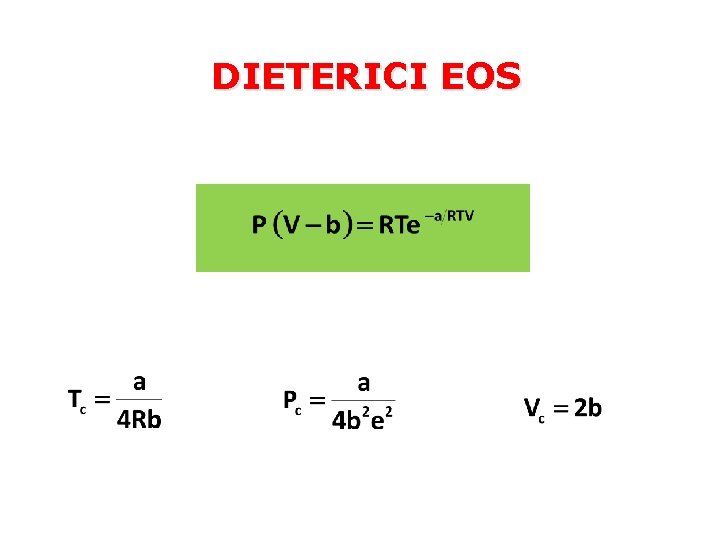
DIETERICI EOS

MIXTURE • For mixtures, we apply the same equation, but we impose certain mixing rules to obtain “a” and “b”, which are functions of the properties of the pure components. • We create a new “pseudo” pure substance that has the average properties of the mixture.