Chapter 2 Dynamic Modeling Process Dynamics Chemical Engineering

Chapter 2 Dynamic Modeling

Process Dynamics • Chemical Engineering courses are generally taught from a steady-state point-of-view. • Dynamics is the time varying behavior of processes. • Chemical processes are dynamically changing continuously. • Steady-state change indicates where the process is going and the dynamic characteristics of a system indicates what dynamic path it will take.

Uses of Dynamic Process Models • Evaluation of process control configurations – For analysis of difficult control systems for both existing facilities and new projects • Process design of batch processes • Operator Training • Start-up/shut-down strategy development

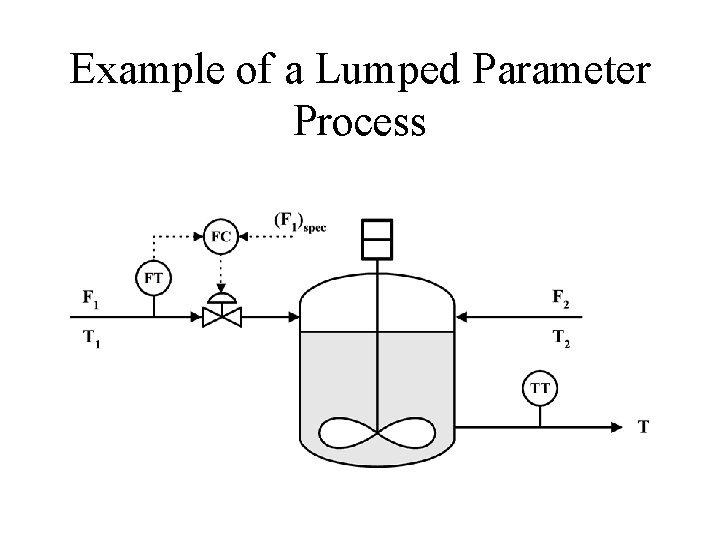
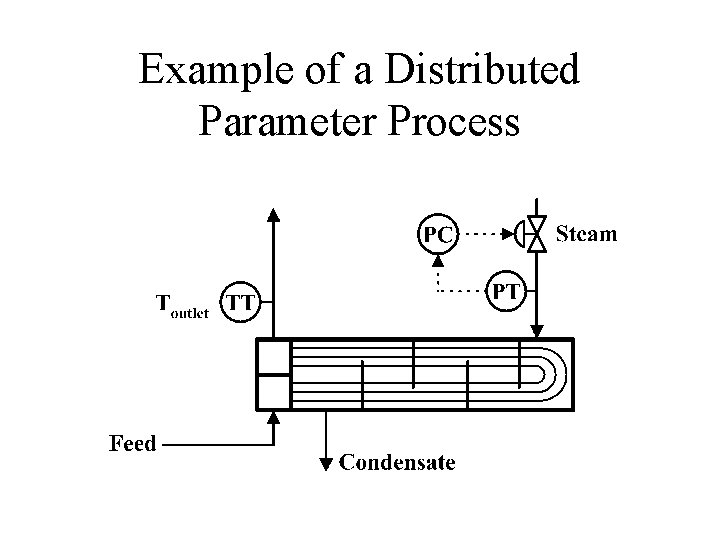
Classification of Models • Lumped parameter models- assume that the dependent variable does not change with spatial location within the process, e. g. , a perfectly well mixed vessel. • Distributed parameter models- consider that the dependent variable changes with spatial location within the process.

Example of a Lumped Parameter Process

Example of a Distributed Parameter Process

Modeling Approaches • Lumped parameter processes- Macroscopic balances are typically applied for conservation of mass, moles, or energy and result in ODE’s. • Distributed parameter processes. Microscopic balances are typically applied yielding differential equations for conservation of mass, moles, or energy for a single point in the process which result in PDE’s.

Conservation Equations: Mass, Moles, or Energy Balances

Mass Balance Equation

Mole Balance Equation

Thermal Energy Balance Equation

Constitutive Relationships • Usually in the form of algebraic equations. • Used with the balance equations to model chemical engineering processes. • Examples include: – Reaction kinetic expressions – Equations of state – Heat transfer correlation functions – Vapor/liquid equilibrium relationships

Degree of Freedom Analysis • The number of degrees of freedom (DOF) is equal to the number of unknowns minus the number of equations. • When DOF is zero, the equations are exactly specified. • When DOF is negative, the system is overspecified. • When DOF is positive, it is underspecified.

Different Types of Modeling Terms • Dependent variables are calculated from the solution of the model equations. • Independent variables require specification by the user or by an optimization algorithm and represent extra degrees of freedom. • Parameters, such as densities or rate constants, are constants used in the model equations.

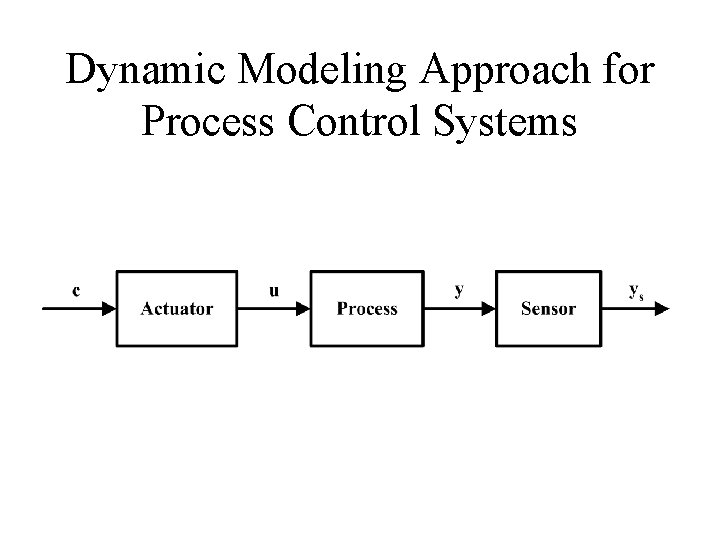
Dynamic Models of Control Systems • Control systems affect the process through the actuator system which has its own dynamics. • The process responds dynamically to the change in the manipulated variable. • The response of the process is measured by sensor system which has its own dynamics. • There are many control systems for which the dynamics of the actuator and sensor systems are important.

Dynamic Modeling Approach for Process Control Systems

Dynamic Model for Actuators • These equations assume that the actuator behaves as a first order process. • The dynamic behavior of the actuator is described by the time constant since the gain is unity

Heat addition as a Manipulated Variable • Consider a steam heated reboiler as an example. • A flow control loop makes an increase in the flow rate of steam to the reboiler. • The temperature of the metal tubes in the reboiler increases in a lagged manner. • The flow rate of vapor leaving the reboiler begins to increase. • The entire process is lumped together into one first order dynamic model.

Dynamic Response of an Actuator (First Order Process)

Dynamic Model for Sensors • These equations assume that the sensors behave as a first order process. • The dynamic behavior of the sensor is described by the time constant since the gain is unity • T and L are the actual temperature and level.

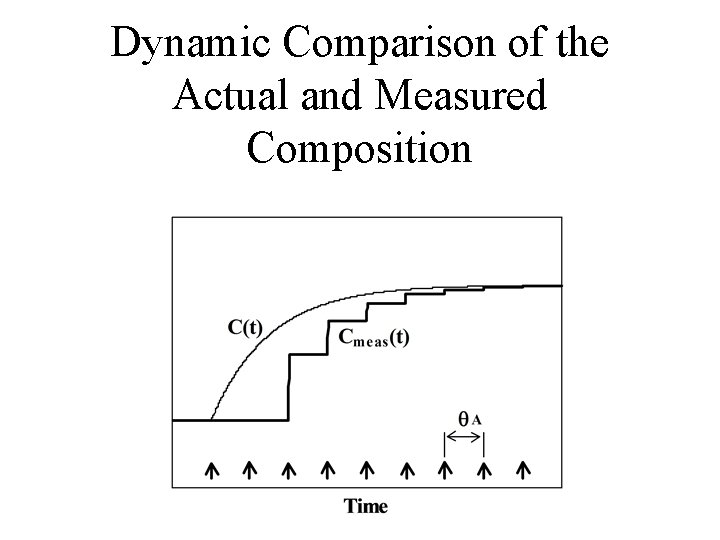
Dynamic Model for an Analyzer • This equation assumes that the analyzer behaves as a pure deadtime element. • The dynamic behavior of the sensor is described by the analyzer deadtime since the gain is unity

Dynamic Comparison of the Actual and Measured Composition

Dynamic Model of a Level in a Tank • Model equation is based on dynamic conservation of mass, i. e. , accumulation of mass in the tank is equal to the mass flow rate into the tank minus the mass flow rate out.

Dynamic Model for Tank Level • Actuator on flow out of the tank. • Process model • Level sensor since the level sensor is much faster than the process and the actuator

Model for Product Composition for CSTR with a Series Reaction

Sensor Noise • Noise is the variation in a measurement of a process variable that does not reflect real changes in the process variable. • Noise is caused by electrical interference, mechanical vibrations, or fluctuations within the process. • Noise affects the measured value of the controlled variable; therefore, it should be included when modeling process dynamics.

Modeling Sensor Noise • Select standard deviation (s) of noise. s is equal to 50% of repeatability. • Generate random number. • Use random number in a correlation for the Gaussian distribution which uses s. This result is the noise on the measurement. • Add the noise to the noise free measurement of the controlled variable.

Numerical Integration of ODE’s • Accuracy and stability are key issues. • Reducing integration step size improves accuracy and stability of explicit integrators • The ODE’s that represent the dynamic behavior of control systems in the CPI are not usually very stiff. • As a result, a Euler integrator is usually the easiest and most effective integrator to use.

Development of Dynamic Process Models for Process Control Analysis • It is expensive, time consuming, and requires a specific expertise. • It is typically only used in special cases for particularly difficult and important processes.

Overview • Dynamic modeling for process control analysis should consider the dynamics of the actuator, the process, and the sensor as well as sensor noise.