Chapter 2 Discrete Random Variables Random Variables Informally

Chapter 2 Discrete Random Variables

Random Variables Informally: A rule for assigning a real number to each outcome of a random experiment – A fish is randomly selected from a lake. Let the random variable Z = the length of the fish in inches – A voter is randomly selected and asked if he or she supports a candidate running for office. Let the random variable

Random Variables Definition 2. 1. 1 Let S be the sample space of a random experiment. A random variable is a function The set of possible values of X is called the range of X (also called the support of X).

Random Variables 1. A random variable is a function. 2. A random variable is not a probability. 3. Random variables can be defined in practically any way. Their values do not have to be positive or between 0 and 1 as with probabilities. 4. Random variables are typically named using capital letters such as X, Y , or Z. Values of random variables are denoted with their respective lower-case letters. Thus, the expression X=x means that the random variable X has the value x.

Discrete Random Variables Definition 2. 1. 2 A random variable is discrete if its range is either finite or countable. Chapter 3 – Continuous random variables

2. 2 – Probability Mass Functions •

Distribution • Definition 2. 2. 2 The distribution of a random variable is a description of the probabilities of the values of variable.

Example 2. 2. 1 A bag contains one red cube and one blue cube. Consider the random experiment of selecting two cubes with replacement. The two cubes we select are called the sample. The same space is S = {RR, RB, BR, BB}, and we assume that each outcome is equally likely. Define the random variable X = the number of red cubes in the sample

Example 2. 2. 1 Values of X: X(RR) = 2, X(RB) = 1, X(BR) = 1, X(BB) = 0 Values of the p. m. f. :
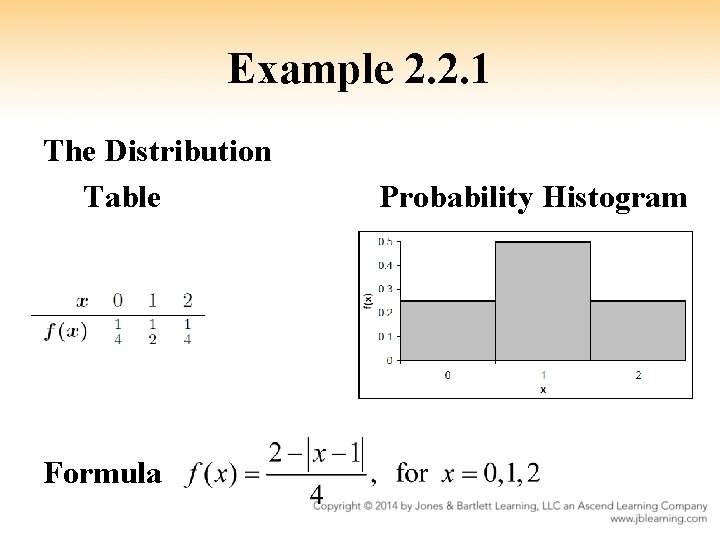
Example 2. 2. 1 The Distribution Table Formula Probability Histogram

Uniform Distribution Definition 2. 2. 3 Let X be a discrete random variable with k elements in its range R. X has a uniform distribution (or be uniformally distributed) if its p. m. f. is

Example 2. 2. 2 Consider the random experiment of rolling a fair six-sided die. The sample space is S ={1, 2, 3, 4, 5, 6} Let the random variable X be the number of dots on the side that lands up. Then (i. e. X has a uniform distribution)

Cumulative Distribution Function Definition 2. 2. 4 The cumulative distribution function (abbreviated c. d. f. ) of a discrete random variable X is

Example 2. 2. 4 Consider the random experiment of rolling two fair six-sided dice and calculating the sum. Let the random variable X be this sum.
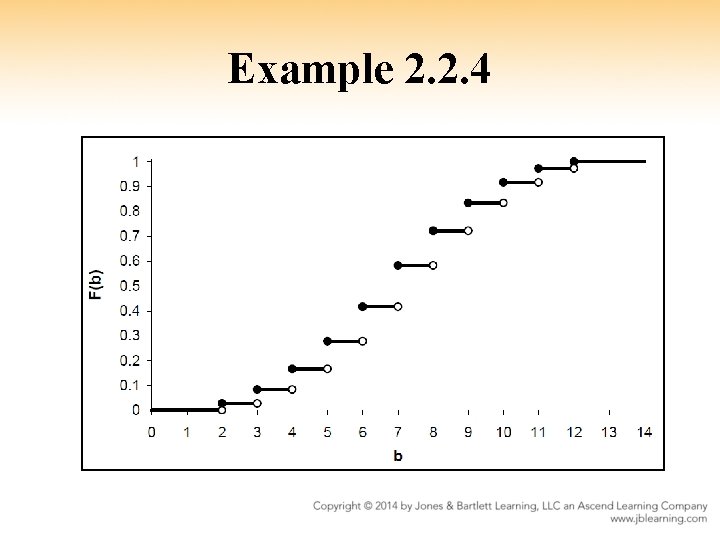
Example 2. 2. 4

Mode and Median • Definition 2. 2. 5 The mode of a discrete random variable X is a value of X at which the p. m. f. f is maximized. The median of X is the smallest number m such that

Example 2. 2. 1 • Mode = 1 • Median = 1 since

2. 3 – Hypergeometric and Binomial Distributions Definition 2. 3. 1 Consider a random experiment that meets the following requirements: 1. We select n objects from a population of N without replacement (n ≤ N). 2. The N objects are of two types, call them type I and type II, where N 1 are of type I and N 2 are of type II (N 1 + N 2 = N). Define the random variable X = the number of type I objects in the sample of n.

Hypergeometric Distribution Definition 2. 3. 1 (continued) Then X has a hypergeometric distribution and its p. m. f. is – The numbers N, n, N 1, and N 2 are called the parameters of the random variable.

Example 2. 3. 2 A manufacturer of radios receives a shipment of 200 transistors, four of which are defective. To determine if they will accept the shipment, they randomly select 10 transistors and test each. If there is more than one defective transistor in the sample, they reject the entire shipment. Find the probability that the shipment is not rejected.

Example 2. 3. 2 • X = number of defectives in the sample of 10 • X has a hypergeometric distribution with N = 200, n = 10, N 1 = 4, and N 2 = 196.

Bernoulli Experiment Definition 2. 3. 2 A random experiment is called a Bernoulli experiment if each outcome is classified into exactly one of two distinct categories. These two categories are often called success and failure. If a Bernoulli experiment is repeated several times in such a way that the probability of a success does not change from one iteration to the next, the experiments are said to be independent. A sequence of n Bernoulli trials is a sequence of n independent Bernoulli experiments.

Binomial Distribution Definition 2. 3. 3 Consider a random experiment that meets the following requirements: 1. A sequence of n Bernoulli trials is performed 2. The probability of a success in any one trial is p Define the random variable X = the number of successes in the n trials

Binomial Distribution Definition 2. 3. 3 (continued) Then X has a binomial distribution and its p. m. f. is – The numbers n and p are the parameters of the distribution – The phrase “X is b(n, p)” means the variable X has a binomial distribution with parameters n and p

Example 2. 3. 4 If a family with nine children is randomly chosen, find the probability of selecting a family with exactly four boys. – Let X = the number of boys in the family – X is b(9, 0. 5)

Unusual Events Unusual Event Principle: If we make an assumption (or a claim) about a random experiment, and then observe an event with a very small probability based on that assumption (called an “unusual event”), then we conclude that the assumption is most likely incorrect.

Unusual Events Unusual Event Guideline: If X is b(n, p) and represents the number of successes in a random experiment, then an observed event consisting of exactly x successes is considered “unusual” if

Example 2. 3. 7 Suppose a university student body consists of 70% females. To discuss ways of improving dormitory policies, the President selects a panel of 15 students. He claims to have randomly selected the students, however, one administrator questions this claim because there are only five females on the panel. Use the rare event principle to test the claim of randomness.

Example 2. 3. 7 • Let X = number of females on the panel of 15 • If randomly selected, then X would be approximately b(15, 0. 7) • Conclusion: Reject the claim of randomness

2. 4 – The Poisson Distribution Definition 2. 4. 1 A random variable X has a Poisson distribution if its p. m. f. is where λ > 0 is a constant. – Describes the number of “occurrences” over a randomly selected “interval” – The parameter λ is the “average” number of occurrences per interval

Example 2. 4. 1 Suppose a 1000 ft 2 lawn contains 3000 dandelions. Find the probability that a randomly chosen 1 ft 2 section of lawn contains exactly five dandelions. – “Occurrence” = dandelion – “Interval” = 1 ft 2 section of lawn – X = number of dandelions in a 1 ft 2 section of lawn – Assume X is Poisson

Example 2. 4. 1

2. 5 – Mean and Variance Definition 2. 5. 1 The mean (or expected value) of a discrete random variable X with range R and p. m. f. f (x) is provided this series converges absolutely

Variance Definition 2. 5. 2 The variance of a discrete random variable X with range R and p. m. f. f (x) is provided this series converges absolutely. The standard deviation of X, denoted σ, is the squareroot of the variance

Example 2. 5. 2 The p. m. f. for a random variable X is Mean

Example 2. 5. 2 Variance

Example 2. 5. 3 Consider a random variable X with range R = {1, 2, …, k} and p. m. f. f (x) = 1/k (X has a uniform distribution) Mean:

Example 2. 5. 3 Variance:

2. 6 – Functions of a Random Variable Example 2. 6. 1: Suppose a man is injured in a car wreck. The doctor tells him that he needs to spend between one and four days in the hospital and that if X is the number of days, its distribution is given below

Example 2. 6. 1 The man’s supplemental insurance policy will give him $500 plus $100 per day in the hospital to cover expenses. How much should the man expect to get from the insurance company? – Y = amount received from the insurance company

Example 2. 6. 1 • Note

Mathematical Expectation Definition 2. 6. 1 Let X be a discrete random variable with range R and p. m. f. f(x). Also let u(X) be a function of X. The mathematical expectation or the expected value of u(X) is provided this series converges absolutely

Example 2. 6. 2 Let X be a random variable with distribution

Properties Theorem 2. 6. 1 Let X be a discrete random. Whenever the expectations exist, the following three properties hold:

Example 2. 6. 3 Let X be a random variable with distribution

2. 7 – Moment-Generating Function Definition 2. 7. 1 Let X be a discrete random variable with p. m. f f(x) and range R. The moment -generating function (m. g. f. ) of X is for all values of t for which this mathematical expectation exists.

Example 2. 7. 1 Consider a random variable X with range R = {2, 5} and p. m. f. f (2) = 0. 25, f (5) = 0. 75 Its m. g. f. is

Theorem 2. 7. 1 If X is a random variable and its m. g. f. M(t) exists for all t in an open interval containing 0, then

Uses of m. g. f. 1. If we know the m. g. f. of a random variable, then we can use the first and second derivatives to find the mean and variance of the variable. 2. If we can show that two random variables have the same m. g. f. , then we can conclude that they have the same distribution.

Example 2. 7. 3 •

Example 2. 7. 3 1. Find the m. g. f.

Example 2. 7. 3 2. Find M’ and M’’ 3. Find mean

Example 2. 7. 3 4. Find variance
- Slides: 53













































































