Chapter 2 Describing Motion Kinematics in One Dimension

Chapter 2: Describing Motion – Kinematics in One Dimension

Terms you should know • Kinematics – how stuff moves • Dynamics – why stuff moves • Translational motion – moving without rotating – Like a car going down the road

It’s all relative • If you are standing still on the road and a car passes you going 45 mi/hr, the car moves away from you at 45 mi/hr (Duh). • But, if you were in a car going 35 mi/hr and a car passes you going 45 mi/hr, how fast does the car move away from you? • It all depends on your FRAME OF REFERENCE

Displacement vs. Distance • Displacement = how far you are from a certain point. • Distance = how far you traveled • These are not always the same thing. • Example – If I drive 150 miles to Houston and 150 miles back home my displacement is zero (I’m back at home) but my distance is 300 miles.

Average Velocity • When talking about how stuff moves, it is usually useful to talk about how fast it is moving. • In everyday language speed and velocity to mean the same thing, but this is not quite right. • Average speed = distance / time • Average velocity = displacement / time

Back to my example • If my whole trip to Houston and back took 4 hours of driving, then my avg. speed = distance / time = 300 mi/4 hr = 75 mi/hr and my avg. velocity = displacement / time = 0 mi / 4 hr = 0 mi/hr

How to calculate displacement • In order to calculate the average velocity of an object you will need to know how to calculate its displacement. • Displacement = final position – initial position • Note – unless it says otherwise, you can make the initial position 0. • Example – If I drive 10 miles from my house then my displacement = 10 mi – 0 mi = 10 mi

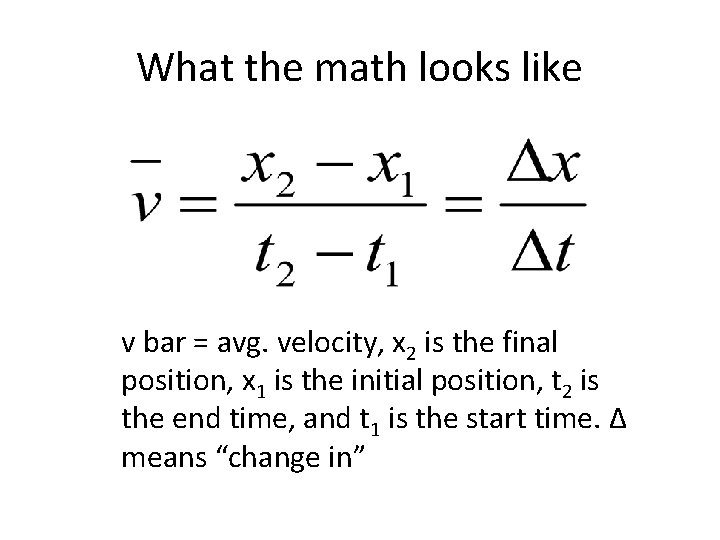
What the math looks like v bar = avg. velocity, x 2 is the final position, x 1 is the initial position, t 2 is the end time, and t 1 is the start time. Δ means “change in”

Example 1 • During a 3. 0 s time interval, a runner’s position changes from 50. 0 m to 30. 5 m. What was the runner’s average velocity?

Solution • Step 1 – given t 2 = 3 s, t 1 = 0 s, x 1 = 50 m, and x 2 = 30. 5 m • Step 2 – we are asked to find the average velocity. • Step 3 – use v = Δx/Δt • Step 4

Example 2 • How far can a cyclist travel in 2. 5 hr in a straight line if her average velocity is 18 km/hr?

Solution • Step 1 – we are given v = 18 km/hr and Δt = 2. 5 hr • Step 2 – we are asked to find distance, Δx • Step 3 – we can rewrite v = Δx/Δt for Δx • Step 4 – Δx = v Δt = 18 km/hr * 2. 5 hr = 45 km • Step 5 – check: v = Δx/Δt does 45 km / 2. 5 hr = 18 km/hr? yes, check.

Your Turn • What must your car’s average velocity be to travel 280 km in 3. 2 hr? • A bird can fly 15 km/hr. How long does it take to fly 75 km?

Acceleration • Sometimes when talking about how an object moves we want to know how fast it can change its velocity. • Acceleration is the term we give to change in velocity per change in time. • Average acceleration = change of velocity / time elapsed

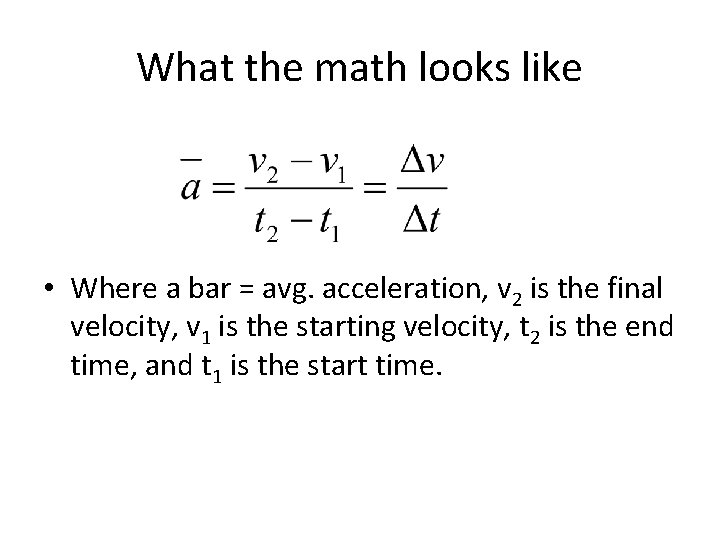
What the math looks like • Where a bar = avg. acceleration, v 2 is the final velocity, v 1 is the starting velocity, t 2 is the end time, and t 1 is the start time.

Example • A car accelerates along a straight road from rest to 75 km/hr in 5. 0 s. What is the magnitude of its average acceleration?

Solution • Step 1 – we are given v 1 = 0 (it says “from rest”), v 2 = 75 km/hr, and Δt = 5. 0 s (t 1 = 0 unless otherwise stated) • Step 2 – we are asked to find the average acceleration. • Step 3 – use • Step 4 -

Example 2 – Deceleration • A car going 15. 0 m/s hits the brakes and slows down to 5. 0 m/s over a period of 5. 0 s. What is the car’s average acceleration?

Solution • Step 1 – we are given v 1 = 15 m/s, v 2 = 5 m/s and Δt = 5. 0 s • Step 2 – we are asked to find the average acceleration. • Step 3 – use • Step 4 –

Your Turn • A sports car accelerates from rest to 95 km/hr in 6. 2 s. What is its average acceleration? What is it in m/s 2?

Motion at constant acceleration • The easiest case to explore is motion where the acceleration is constant, so we will begin there. • If I am accelerating steadily, then my final velocity depends on 3 things: my starting speed, my acceleration, and how long I accelerated for. • v = v 0 + at

Constant acceleration cont. • Likewise, distance traveled will depend on where I started, how fast I traveled, and for how long I traveled. • x = x 0 + • Because velocity is changing steadily, then the average velocity is just the mathematical average.

Combine ‘em • We can combine our last 3 equations to get a very useful equation.

Last one I promise • If we rewrite v = v 0 + at for t, we get t = (v – v 0) / a • If we plug this in for t in x = x 0 + we get our final equation:

The 4 kinematic equations • v = v 0 + at • These 4 equations govern all motion (for constant acceleration)

Example • You are designing an airport for small planes. One type of plane that will use the runway must reach a take off speed of 27. 8 m/s and can accelerate at a rate of 2. 0 m/s 2. If the runway is 150 m long can the plane reach take off speed? If not, what is the minimum length the runway must be?

Solution 1 • Step 1: given: x 0 = 0 m, v 0 = 0 m/s, x = 150 m, and a = 2. 0 m/s 2 • Step 2: what is v? • Step 3: need to use v 2 = v 02 + 2 a(x – x 0) • Step 4: v 2 = 0 + 2(2. 0 m/s 2)(150 m – 0 m) = 600 m 2/s 2 v = √(600 m 2/s 2) = 24. 5 m/s • So the runway is too short and the plane would crash!

Solution 2 • Step 1: given: x 0 = 0 m, v 0 = 0 m/s, v = 27. 8 m/s, and a = 2. 0 m/s 2 • Step 2: we are asked to find x • Step 3: we need to solve v 2 = v 02 + 2 a(x – x 0) for x • Step 4: (x – x 0) = (v 2 – v 02)/2 a =

Example • How long does it take a car to cross a 30. 0 m wide intersection after the light turns green, if it accelerates from rest at a rate of 2. 0 m/s 2?

Solution • • Step 1: given: x 0 = 0 m, v 0 = 0 m/s, a = 2. 0 m/s 2 Step 2: asked to find t Step 3: we should use Step 4: x = 0 + ½at 2 so t 2 = 2 x/a so t = √(2 x/a) = √(2*30 m / 2. 0 m/s 2) = 5. 48 s

Your turn • A car accelerates from 12 m/s to 21 m/s in 6. 0 s. What was its acceleration? How far did it travel in this time?

Practice makes perfect • A car slows down from 25 m/s to rest in a distance of 75 m. What was its acceleration?

Falling Bodies • The kinematic equations still apply in the vertical direction with a few tweaks. • Change all x’s to y’s (for the y axis) • Change a to g, g is the acceleration due to gravity and g = 9. 8 m/s 2

Example • A ball is dropped from a tower that is 70. 0 m high. How far will it have fallen after 2. 0 s? Assume y is positive in the down direction.

Solution • Step 1 – given: y 0 = 0 m, v 0 = 0, t = 2 s, and a = g = 9. 8 m/s 2 • Step 2 – How far will it fall = y • Step 3 – use y = y 0 + v 0 t + ½at 2 • Step 4 – y = 0 + ½(9. 8 m/s 2)(2 s)2 = 19. 6 m

The Man of Steel • In the original comics, Superman could not fly, he just jumped really high. • It was said his max jump was about 200 m (easily the height of a “tall building” back then) • What take off speed does Superman need to reach 200 m?

Additional Practice • A car is capable of an acceleration of 1. 6 m/s 2. At this rate, how long does it take to accelerate from 80 km/h to 110 km/hr?

Practice Problem 2 • A sport’s car is advertised to be able to stop in a distance of 55 m from a speed of 100 km/hr. What is its acceleration in m/s 2? How many g’s is this?

Practice Problem 3 • A light plane must reach a speed of 32 m/s for take off. How long a runway is needed if the acceleration is 3. 0 m/s 2?

Practice Problem 4 • A world-class sprinter can reach a top speed of about 11. 5 m/s in the first 15. 0 m of a race. What is the average acceleration of this sprinter and how long does it take her to reach that speed?

Practice Problem 5 • In coming to a stop, a car leaves a skid mark 75 m long on the highway. Assuming a deceleration of 7. 00 m/s 2, estimate the speed of the car just before breaking.

Practice Problem 6 • A car traveling at 95 km/hr hits a tree. The front end of the car compresses and the driver comes to a rest after traveling 0. 80 m. What was the average acceleration of the driver during the collision? What is this in g’s?

Practice Problem 7 • A stone is dropped from the top of a cliff. It is seen to hit the ground after 2. 75 s. How high was the cliff?

Practice Problem 8 • The best rebounders in the NBA have a vertical leap of about 120 cm. A) What is their initial launch speed? B) How long are they in the air?