Chapter 2 Describing Motion in One Dimension Position

Chapter 2 Describing Motion in One Dimension

Position and Displacement The displacement of an object (or particle) is defined as the change in its position, x (or y, s, etc. ) : Displacement can be positive or negative depending on which direction the position has changed. Usually we take a move to the right as positive and a move to the left as negative.

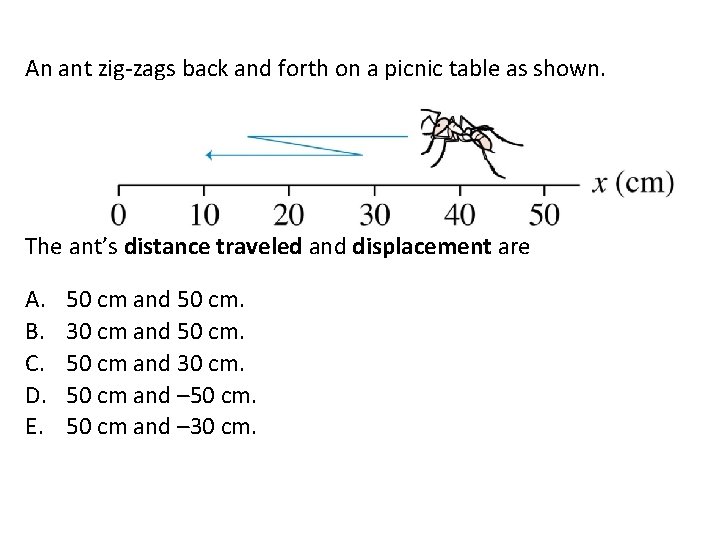
An ant zig-zags back and forth on a picnic table as shown. The ant’s distance traveled and displacement are A. B. C. D. E. 50 cm and 50 cm. 30 cm and 50 cm and 30 cm. 50 cm and – 30 cm.

Average Speed The average speed of an object (or particle) is defined as the total distance traveled by the object divided by the total time of the motion: The SI units for average speed is m/s. Note: average speed is always positive. Note: average speed is not the arithmetic mean of the speed of an object (if it changes)

Quick Example A car travels at an average speed of 55 km/hr for 1. 30 hours and then 65 km/hr for 0. 73 hours. a) What is the total distance travelled by the car? b) What is the average speed for the trip? Technically, we should report 2 sig figs, but 3 is still appropriate (and will be on your homework)

Average Velocity The average velocity of an object (or particle) is defined as the displacement over the time interval: The SI units for average velocity is m/s. Usually we take the average velocity as positive when the object moves to the right and negative when it moves to the left. Velocity is NOT the same as speed!

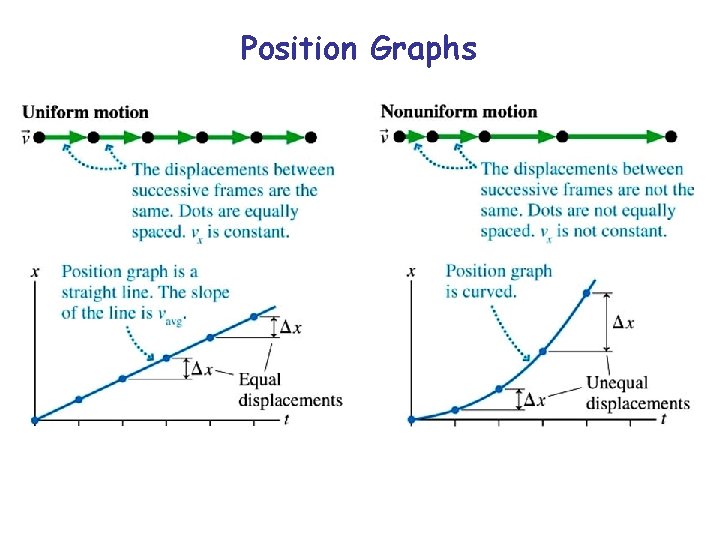
Position Graphs

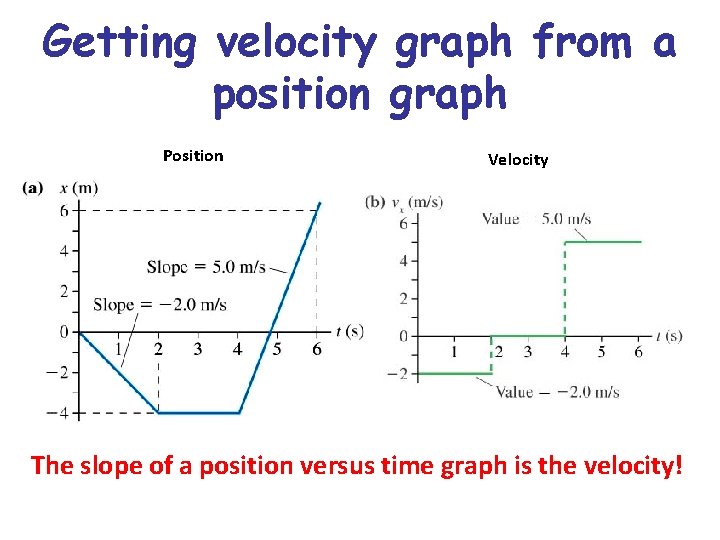
Getting velocity graph from a position graph Position Velocity The slope of a position versus time graph is the velocity!

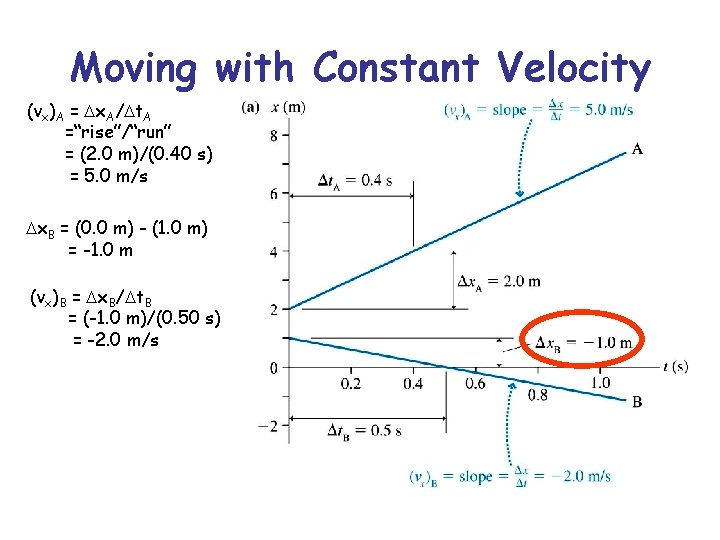
Moving with Constant Velocity (vx)A = x. A/ t. A =“rise”/“run” = (2. 0 m)/(0. 40 s) = 5. 0 m/s x. B = (0. 0 m) - (1. 0 m) = -1. 0 m (vx)B = x. B/ t. B = (-1. 0 m)/(0. 50 s) = -2. 0 m/s

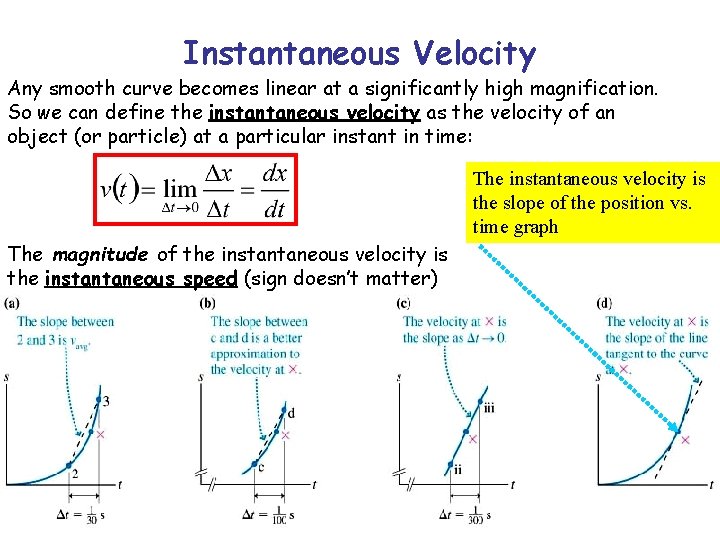
Instantaneous Velocity Any smooth curve becomes linear at a significantly high magnification. So we can define the instantaneous velocity as the velocity of an object (or particle) at a particular instant in time: The instantaneous velocity is the slope of the position vs. time graph The magnitude of the instantaneous velocity is the instantaneous speed (sign doesn’t matter)

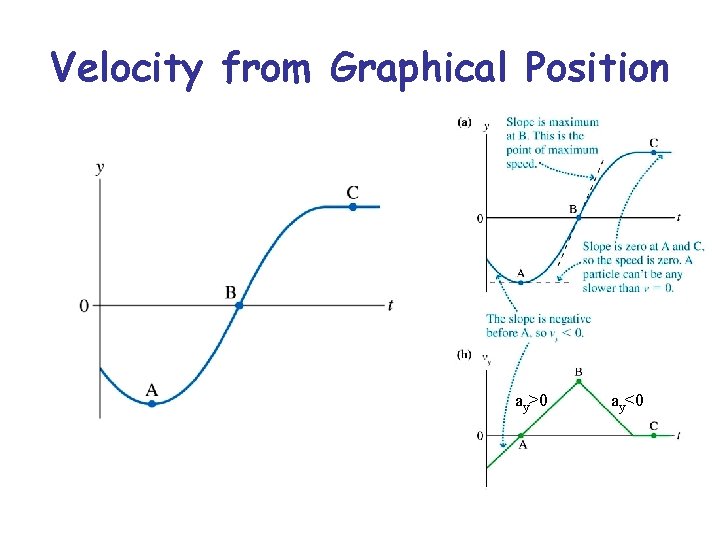
Velocity from Graphical Position ay>0 ay<0

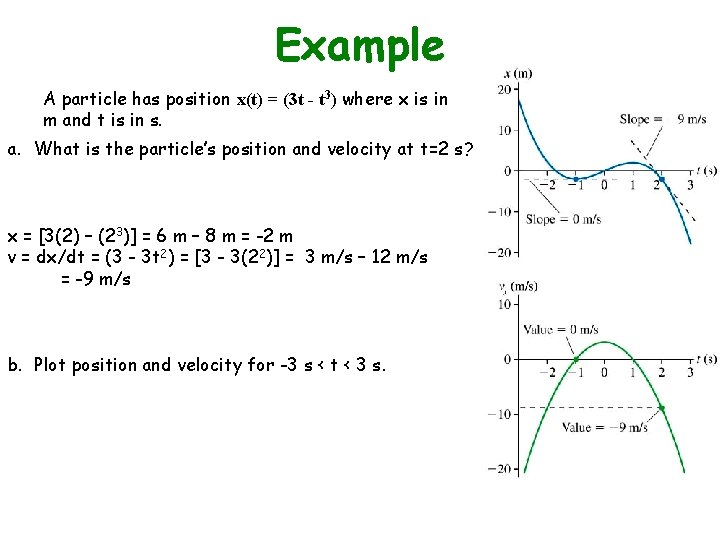
Example A particle has position x(t) = (3 t - t 3) where x is in m and t is in s. a. What is the particle’s position and velocity at t=2 s? x = [3(2) – (23)] = 6 m – 8 m = -2 m v = dx/dt = (3 - 3 t 2) = [3 - 3(22)] = 3 m/s – 12 m/s = -9 m/s b. Plot position and velocity for -3 s < t < 3 s.

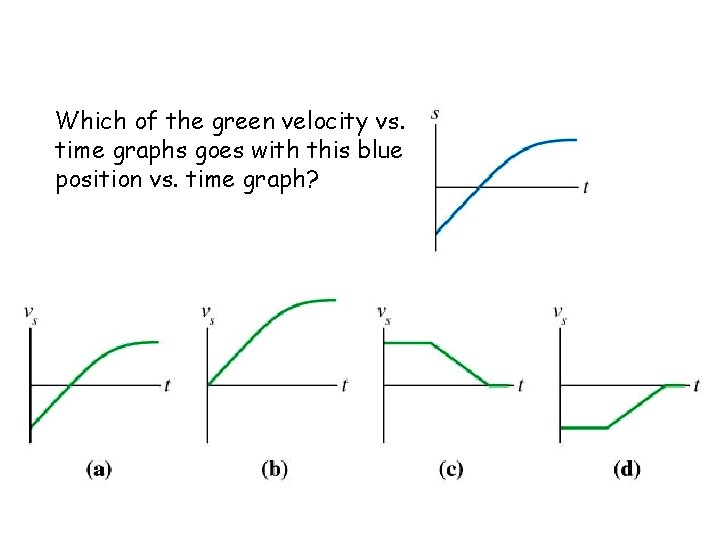
Which of the green velocity vs. time graphs goes with this blue position vs. time graph?

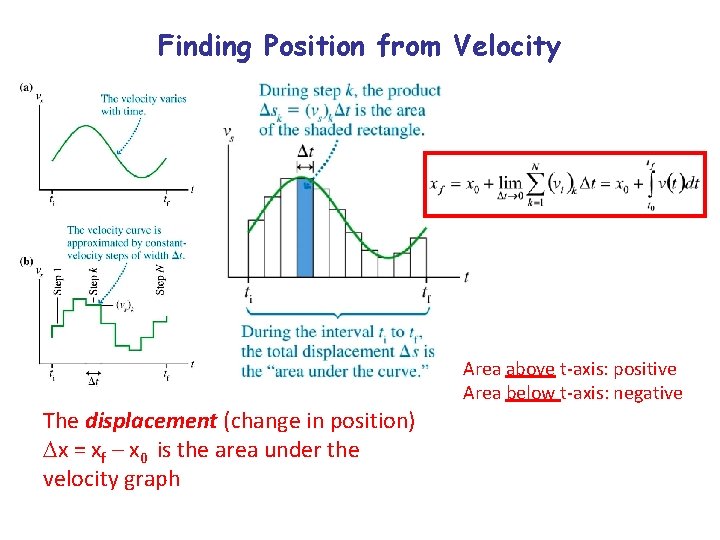
Finding Position from Velocity Area above t-axis: positive Area below t-axis: negative The displacement (change in position) x = xf – x 0 is the area under the velocity graph

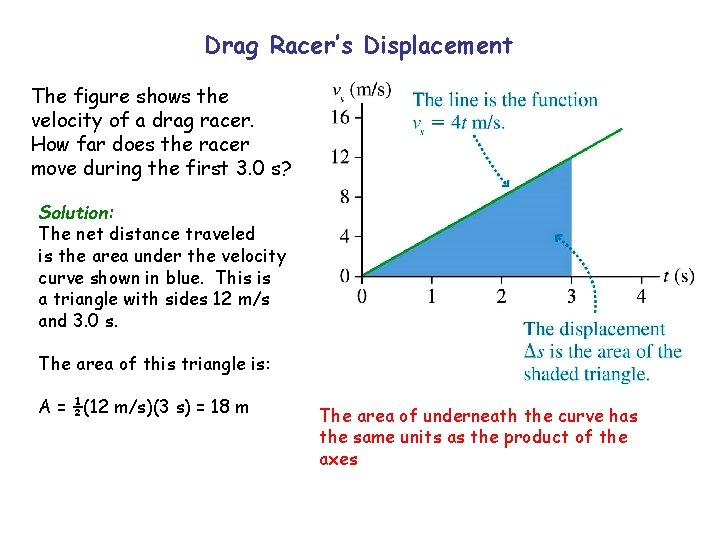
Drag Racer’s Displacement The figure shows the velocity of a drag racer. How far does the racer move during the first 3. 0 s? Solution: The net distance traveled is the area under the velocity curve shown in blue. This is a triangle with sides 12 m/s and 3. 0 s. The area of this triangle is: A = ½(12 m/s)(3 s) = 18 m The area of underneath the curve has the same units as the product of the axes

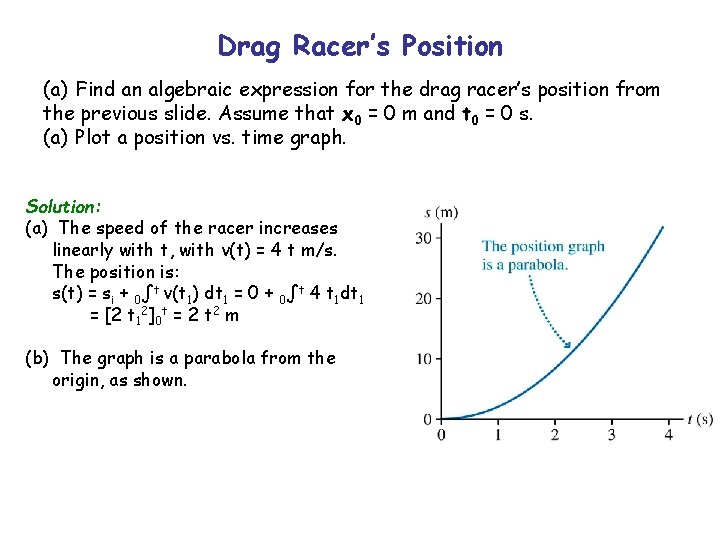
Drag Racer’s Position (a) Find an algebraic expression for the drag racer’s position from the previous slide. Assume that x 0 = 0 m and t 0 = 0 s. (a) Plot a position vs. time graph. Solution: (a) The speed of the racer increases linearly with t, with v(t) = 4 t m/s. The position is: s(t) = si + 0∫t v(t 1) dt 1 = 0 + 0∫t 4 t 1 dt 1 = [2 t 12]0 t = 2 t 2 m (b) The graph is a parabola from the origin, as shown.

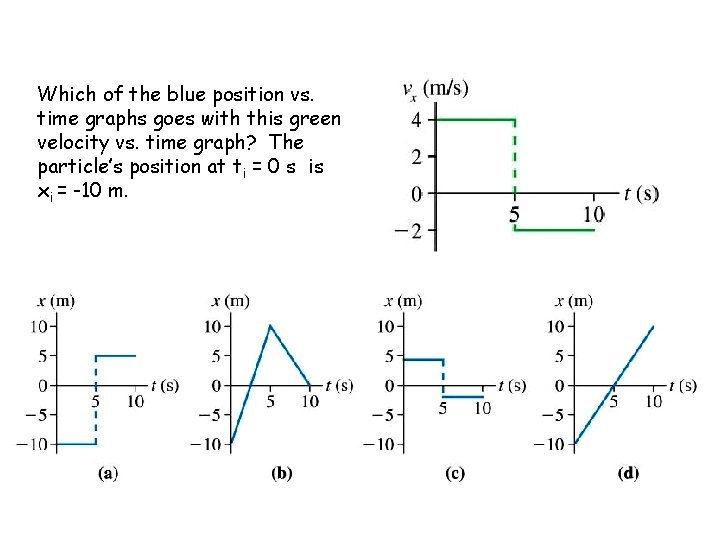
Which of the blue position vs. time graphs goes with this green velocity vs. time graph? The particle’s position at ti = 0 s is xi = -10 m.

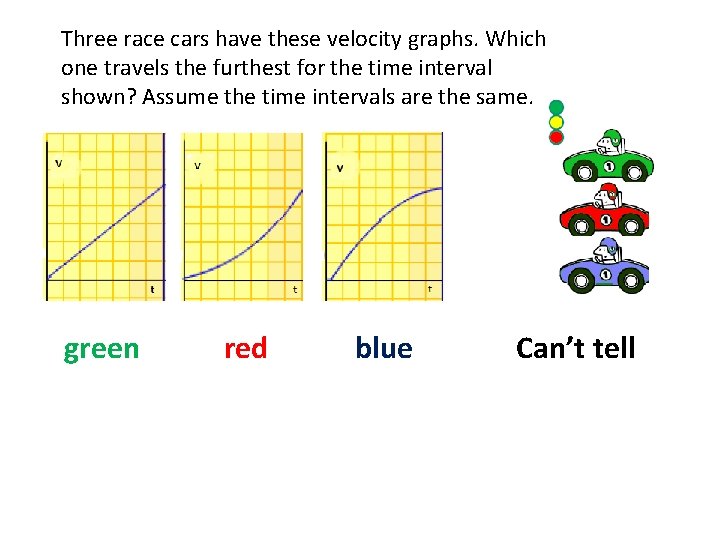
Three race cars have these velocity graphs. Which one travels the furthest for the time interval shown? Assume the time intervals are the same. green red blue Can’t tell

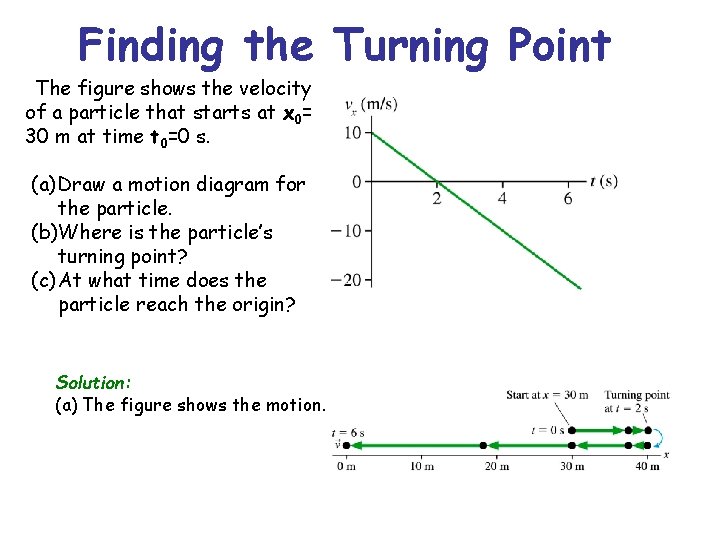
Finding the Turning Point The figure shows the velocity of a particle that starts at x 0= 30 m at time t 0=0 s. (a) Draw a motion diagram for the particle. (b)Where is the particle’s turning point? (c) At what time does the particle reach the origin? Solution: (a) The figure shows the motion.

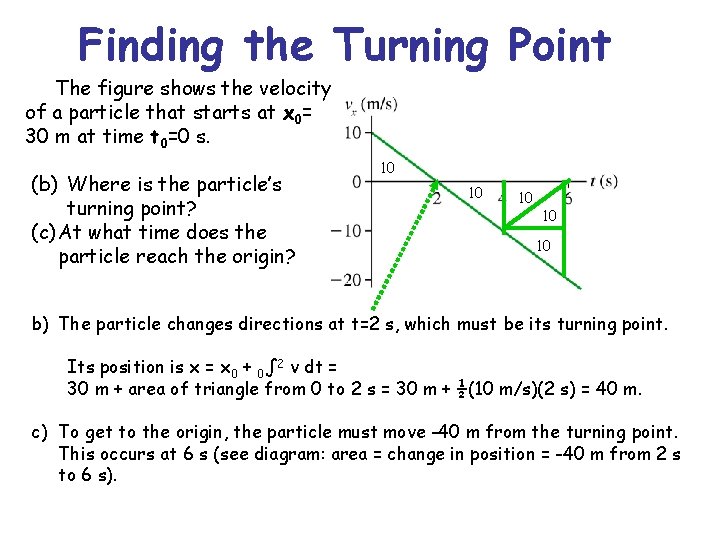
Finding the Turning Point The figure shows the velocity of a particle that starts at x 0= 30 m at time t 0=0 s. (b) Where is the particle’s turning point? (c) At what time does the particle reach the origin? 10 10 10 b) The particle changes directions at t=2 s, which must be its turning point. Its position is x = x 0 + 0∫ 2 v dt = 30 m + area of triangle from 0 to 2 s = 30 m + ½(10 m/s)(2 s) = 40 m. c) To get to the origin, the particle must move -40 m from the turning point. This occurs at 6 s (see diagram: area = change in position = -40 m from 2 s to 6 s).

Average Acceleration The average acceleration of an object is defined as the change of its velocity over time: The SI units for average acceleration is m/s 2 (or m/s/s) A velocity can change when the speed changes and/or the direction changes (it is still a vector!). Again, average acceleration is positive if it points to the right and negative if it points to the left.

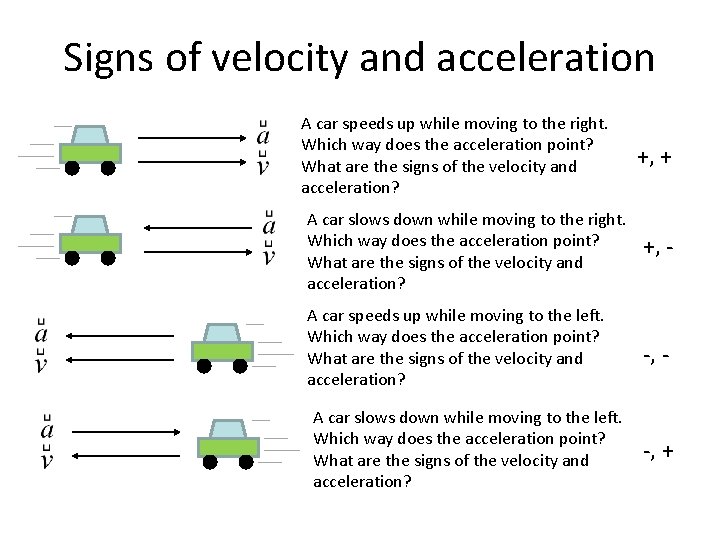
Signs of velocity and acceleration A car speeds up while moving to the right. Which way does the acceleration point? What are the signs of the velocity and acceleration? +, + A car slows down while moving to the right. Which way does the acceleration point? What are the signs of the velocity and acceleration? +, - A car speeds up while moving to the left. Which way does the acceleration point? What are the signs of the velocity and acceleration? -, - A car slows down while moving to the left. Which way does the acceleration point? What are the signs of the velocity and acceleration? -, +

Galileo was the first to analyze motion in terms of measurements and mathematics. He described acceleration, which is the rate of change of velocity. It has units of m/s 2 so an acceleration of 10 m/s 2 means the velocity is changing by 10 m/s every second. Galileo, age 60, drawn by contemporary Ottavio Leoni in 1624.

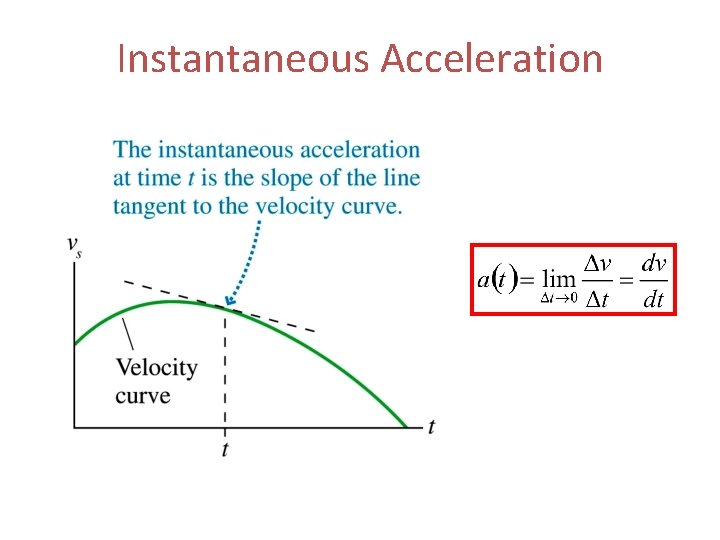
Instantaneous Acceleration

Velocity from Acceleration The area under an a vs. t graph gives the change in the object’s velocity. What is v for the first 8 s?

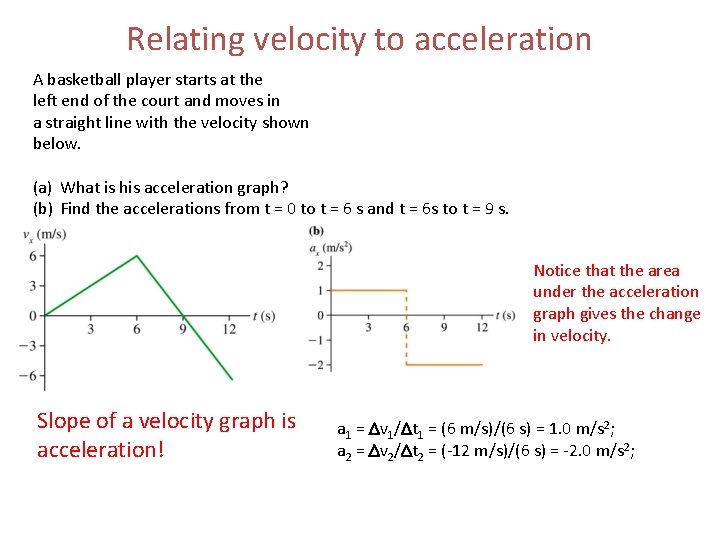
Relating velocity to acceleration A basketball player starts at the left end of the court and moves in a straight line with the velocity shown below. (a) What is his acceleration graph? (b) Find the accelerations from t = 0 to t = 6 s and t = 6 s to t = 9 s. Notice that the area under the acceleration graph gives the change in velocity. Slope of a velocity graph is acceleration! a 1 = Dv 1/Dt 1 = (6 m/s)/(6 s) = 1. 0 m/s 2; a 2 = Dv 2/Dt 2 = (-12 m/s)/(6 s) = -2. 0 m/s 2;

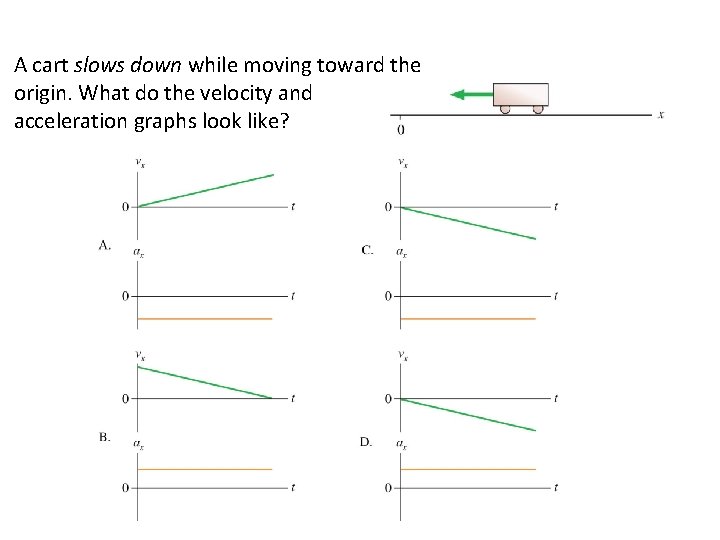
A cart slows down while moving toward the origin. What do the velocity and acceleration graphs look like?

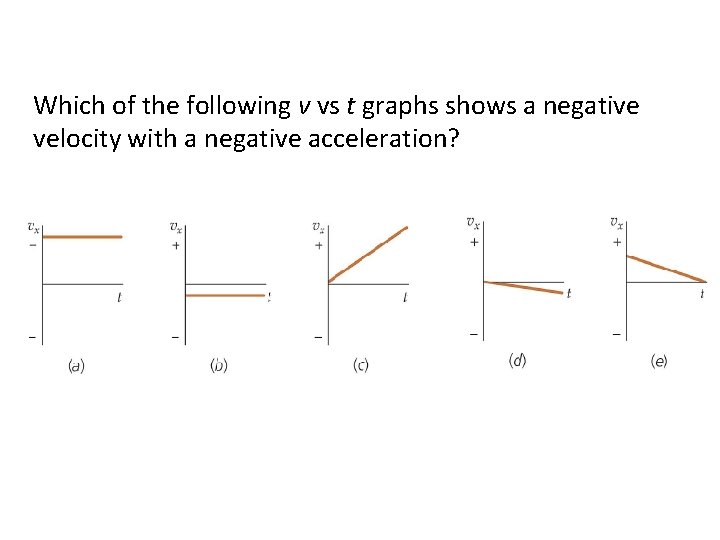
Which of the following v vs t graphs shows a negative velocity with a negative acceleration?

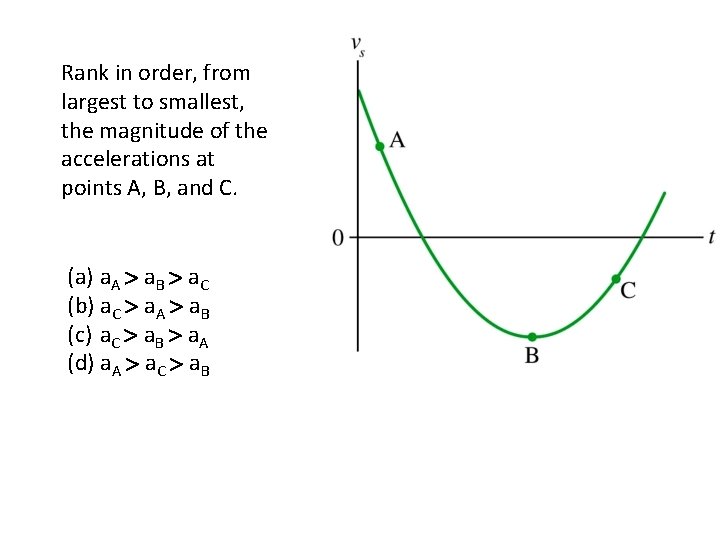
Rank in order, from largest to smallest, the magnitude of the accelerations at points A, B, and C. (a) a. A > a. B > a. C (b) a. C > a. A > a. B (c) a. C > a. B > a. A (d) a. A > a. C > a. B

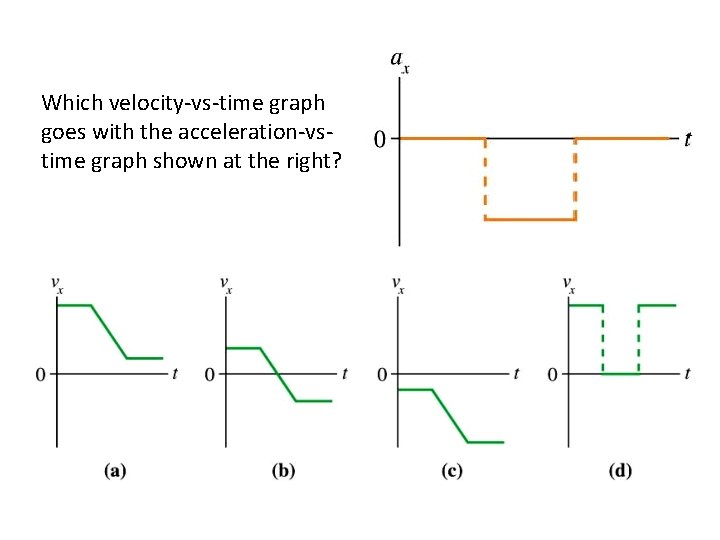
Which velocity-vs-time graph goes with the acceleration-vstime graph shown at the right?

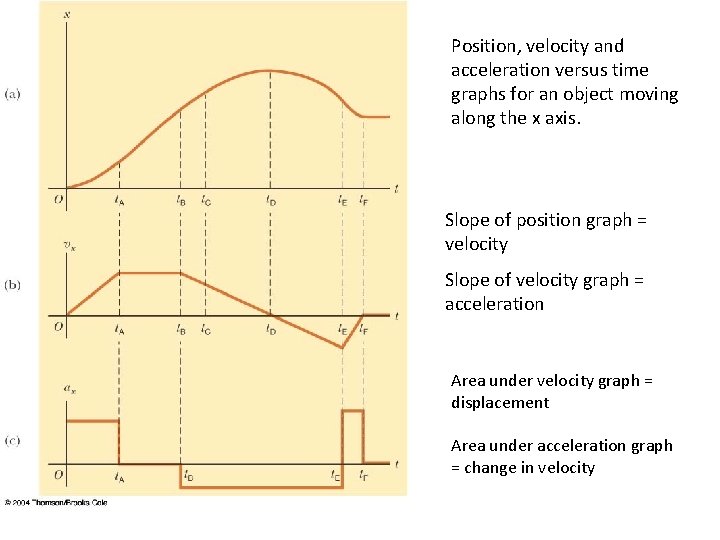
Position, velocity and acceleration versus time graphs for an object moving along the x axis. Slope of position graph = velocity Slope of velocity graph = acceleration Area under velocity graph = displacement Area under acceleration graph = change in velocity

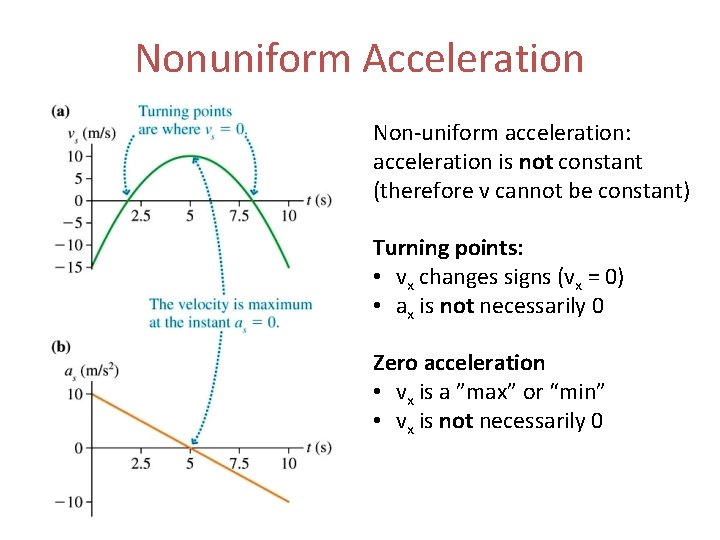
Nonuniform Acceleration Non-uniform acceleration: acceleration is not constant (therefore v cannot be constant) Turning points: • vx changes signs (vx = 0) • ax is not necessarily 0 Zero acceleration • vx is a ”max” or “min” • vx is not necessarily 0

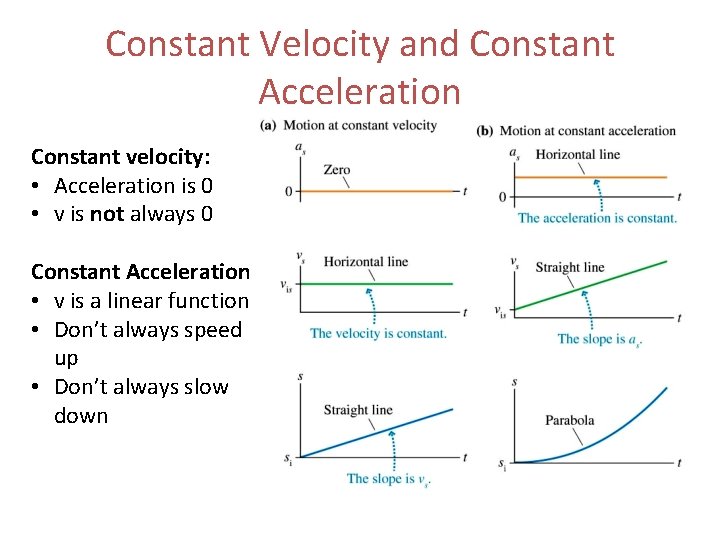
Constant Velocity and Constant Acceleration Constant velocity: • Acceleration is 0 • v is not always 0 Constant Acceleration • v is a linear function • Don’t always speed up • Don’t always slow down

Kinematic Equations The coordinate s is a general coordinate. We can replace s with x or y if our motion is horizontal or vertical, respectively. If the acceleration is not constant, we need to: 1. Break the problem up into parts with constant acceleration 2. Use another method (calculus, graphs).

Rocket Sled A rocket sled accelerates at 50 m/s 2 for 5. 0 s, maintains a constant velocity for 3. 0 s, then deploys a braking parachute and decelerates at 3. 0 m/s 2 until coming to a halt. (a) What is the maximum velocity reached by the rocket sled? (b) What is the total distance traveled by the rocket sled? Given: Δt 1= 5. 0 s Δt 2= 3. 0 s V 0 = 0 V 3 = 0 Find: X 0 =0 a 1 = 50 m/s 2 a 3 = -3. 0 m/s 2 X 1 X 2 X 3 V 1 , x 3 x 1 = x 01 + v 0 t 1 + ½a 1 t 12 = ½a 1 (Δt 1)2 = ½(50 m/s 2)(5. 0 s)2 = 625 m v 1 = v 0 + a 1 t 1= a 1 t 1 = (50 m/s 2)(5. 0 s) = 250 m/s x 2 = x 1 + v 1(Δt 2) = 625 m + (250 m/s)(3. 0 s) = 1, 375 m v 32 = v 12 + 2 a 3 Dx = v 12 +2 a 3(x 3 – x 2), so x 3 = x 2 + (v 32 – v 12)/2 a 3 = 1, 375 m + [0 – (250 m/s)2]/[2(-3. 0 m/s 2)] = 11, 800 m

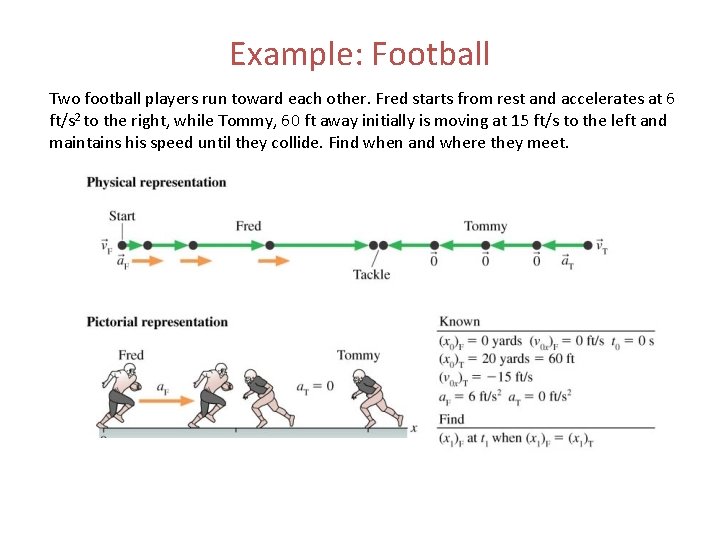
Example: Football Two football players run toward each other. Fred starts from rest and accelerates at 6 ft/s 2 to the right, while Tommy, 60 ft away initially is moving at 15 ft/s to the left and maintains his speed until they collide. Find when and where they meet.

Football Want to find the time and the location where Tommy and Fred meet. Write out kinematic equations for their positions (KE #2 works for both) Fred: xf(F) = 0 + (0) t + ½ (6)t 2 = 3 t 2 Units are ft, ft/s 2 Tommy: xf(T) = 60 + (-15)t To find t, set the position equations equal to each other and solve: 60 + (-15)t = 3 t 2 + 15 t – 60 = 0 t = 2. 62 s, -7. 62 s Substitute t into either position equation to get the final position xf(T) = 60 ft + (-15 ft/s)(2. 62 s) xf(T) = 20. 7 ft

1624 drawing of Galileo at age 60 by Ottavio Leoni Galileo did experiments to convince others that the acceleration caused by gravity would be the same for all freely falling objects if there was no air to retard their motion. He dropped two heavy metal balls together from the leaning tower in Pisa, Italy. Although one weighed far more than the other, they reached the ground almost at the same time.

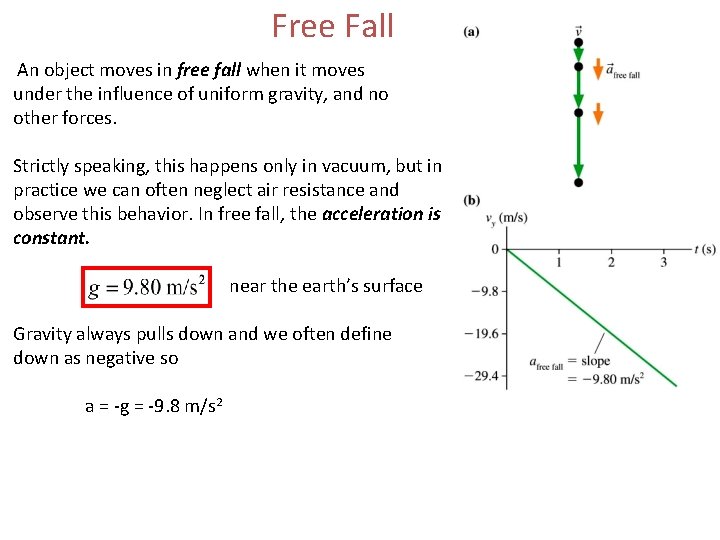
Free Fall An object moves in free fall when it moves under the influence of uniform gravity, and no other forces. Strictly speaking, this happens only in vacuum, but in practice we can often neglect air resistance and observe this behavior. In free fall, the acceleration is constant. near the earth’s surface Gravity always pulls down and we often define down as negative so a = -g = -9. 8 m/s 2

A tennis ball and a golf ball dropped sideby-side in air. The tennis ball is affected more by the air’s resistance than the golf ball. The larger the object is, and the faster it is falling, the greater the air’s resistance to its motion. But for some objects moving at low speeds, air resistance can often be neglected.

When most of the air is removed from a container, feathers and apples fall almost side-by-side, their speeds changing at almost the same rate. If all the air were removed, they would accelerate downward at exactly the same rate. Apple and feather falling in a vacuum.

Apollo 15 astronaut David Scott tested Galileo’s Law of Falling Bodies on the surface of the Moon, standing beside the lunar lander Falcon. With no atmosphere on the Moon, a hammer and a feather fall with the same acceleration. http: //www. youtube. com/watch? v=4 m. Tsr. RZEMw. A

A Falling Rock A rock is released from rest at the top of a 100 m tall building. (a) How long does to take for the rock to fall to the ground? yf = yi + vit + ½at 2 , so t = [2(yf - yi)/a]½ = [2(-100 m)/(-9. 80 m/s 2)]½ = ± 4. 52 s = 4. 52 s Given: (b) What is the impact velocity? a = -g = -9. 8 m/s 2 vf = vi + at = 0 – (9. 80 m/s 2)(4. 52 s) = -44. 3 m/s Yi= 100 m vi = yf = 0 Find: t, vf

An apple is tossed straight up in the air. Does it speed up, slow down or move at a constant speed? What is the velocity of the apple when it is at its highest point? What is the acceleration of the apple as it falls?

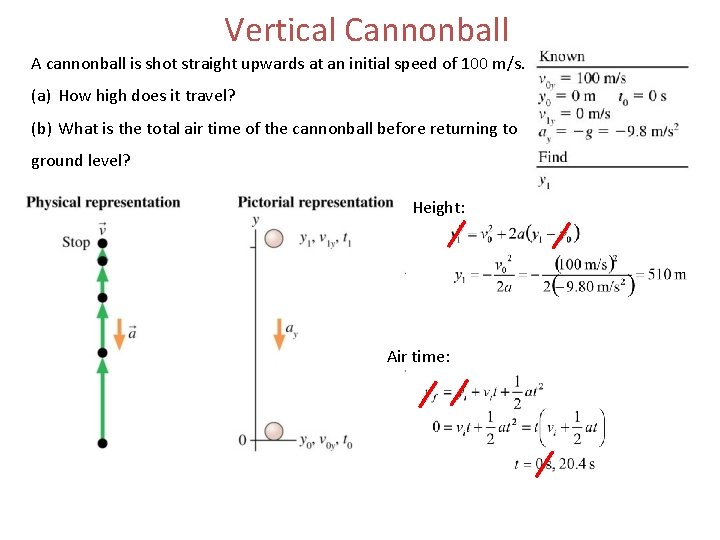
Vertical Cannonball A cannonball is shot straight upwards at an initial speed of 100 m/s. (a) How high does it travel? (b) What is the total air time of the cannonball before returning to ground level? Height: Air time:

Alice and Bill are at the top of a building. Alice throws her ball downward. Bill simply drops his ball. Which ball has the greater acceleration just after release? A) Alice’s ball B) it depends on how hard the ball was thrown C) neither -- they both have the same acceleration D) Bill’s ball Alice v 0 v. A Bill v. B

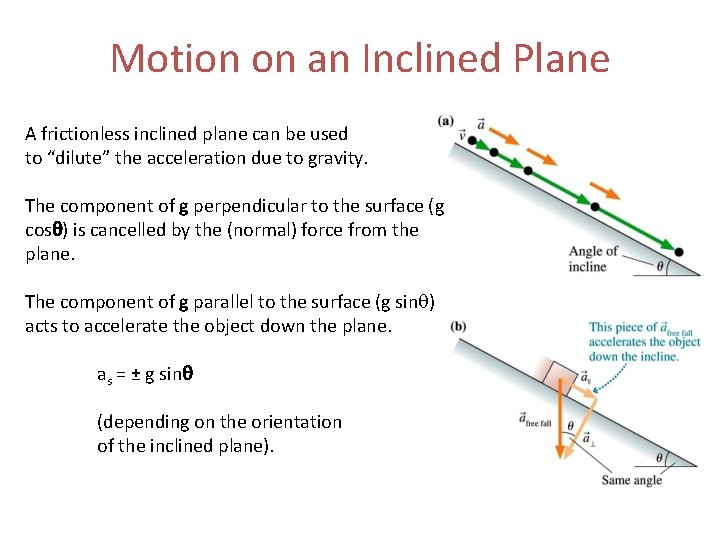
Motion on an Inclined Plane A frictionless inclined plane can be used to “dilute” the acceleration due to gravity. The component of g perpendicular to the surface (g cosq) is cancelled by the (normal) force from the plane. The component of g parallel to the surface (g sinq) acts to accelerate the object down the plane. as = ± g sinq (depending on the orientation of the inclined plane).

Downhill Skiing A skier’s speed at the bottom of a 100 m slope is 20 m/s. What is the angle of the slope? Assume the skier started from rest. Use kinematic eq. #3: v 1 s 2 = v 0 s 2 + 2 as s = 2 g sinq s so sinq = v 1 s 2/(2 g s) = (20 m/s)2/[2(9. 80 m/s 2)(100 m)] = 0. 204 q = sin-1(0. 204) = 11. 8 O

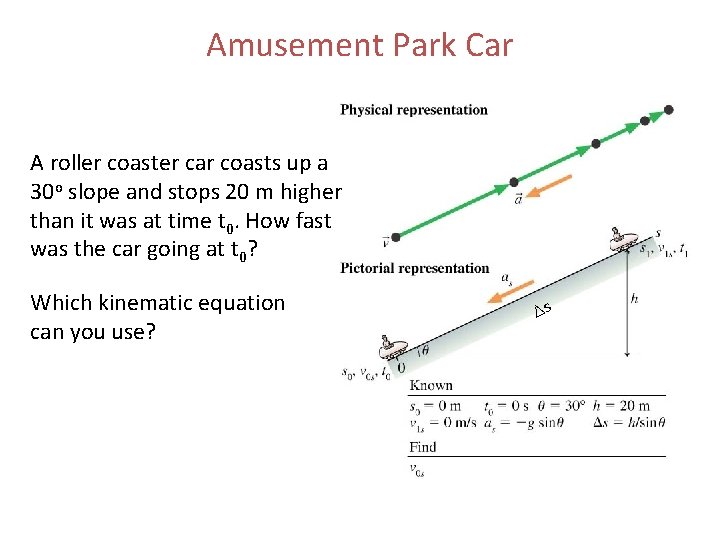
Amusement Park Car A roller coaster car coasts up a 30 o slope and stops 20 m higher than it was at time t 0. How fast was the car going at t 0? Which kinematic equation can you use? s

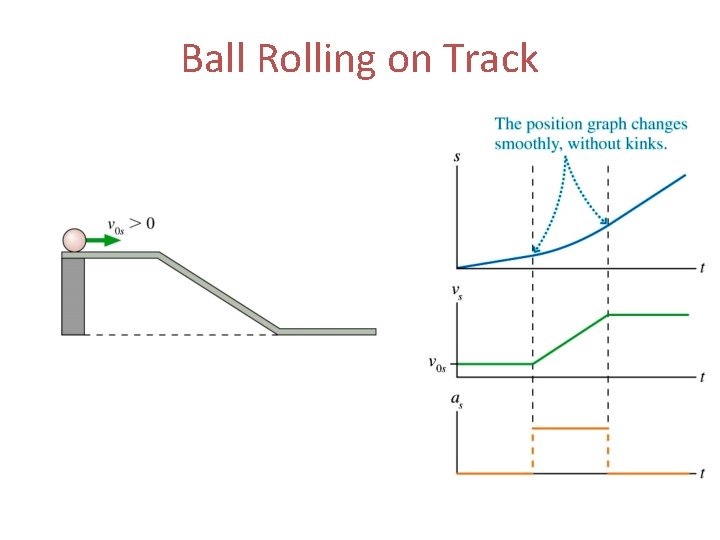
Ball Rolling on Track

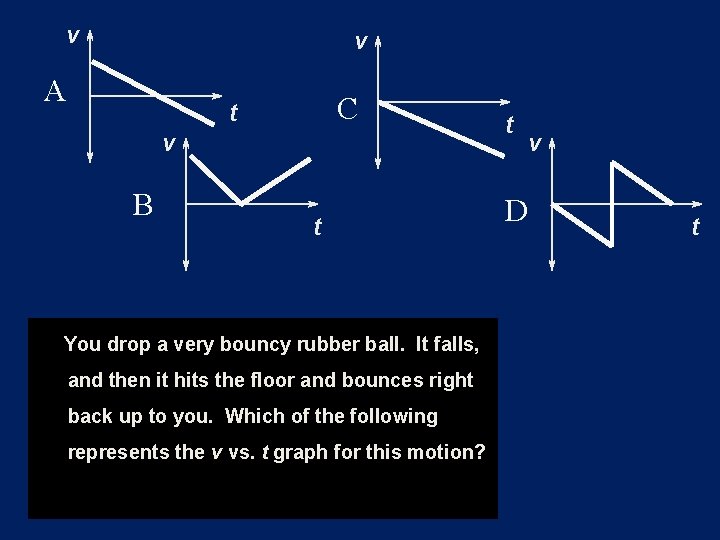
v v A C t v B t You drop a very bouncy rubber ball. It falls, and then it hits the floor and bounces right back up to you. Which of the following represents the v vs. t graph for this motion? t v D t